С.Н.Портнов
Сергей Портнов заинтересовался механизмами образования торнадо и смерчей и в ходе изучения этого вопроса наткнулся на информацию об устройствах Виктора Шаубергера... И углубился в эту тему. Результаты, на мой взгляд, заслуживают самого широкого освещения!
Для связи с автором можно использовать почту bbbox@yandex.ru. Кроме того, летом 2013 года он открыл свой сайт http://si-is.ucoz.ru, где публикует новые материалы. Рекомендую ознакомиться!
«Освобождённая энергия»
«Механика Творца»
Это не статья, а целая книга. На сайте я с разрешения автора публикую лишь её фрагмент, касающийся результатов поставленных автором опытов по истечению воды через спиральные сопла. Но я уверен, что это не самая ценная и не самая интересная часть этой книги. Подходы, применённые автором к анализу работ и аппаратов Шаубергера, мне до сих пор не встречались. Причём выдвинутые идеи с научной точки зрения разработаны весьма глубоко. Поэтому рекомендую эту книгу не только тем, кто занимается идеями и установками Шаубергера, но и всем, интересующимся проблемой «свободной энергии» в целом. С разрешения автора я выложил на сайте полную авторскую версию этой книги, которую Вы можете бесплатно скачать в формате pdf (файл liberate.pdf, 4524640 байт).
Перед публикацией мы с автором несколько месяцев обсуждали книгу в переписке. Не все мысли автора я поддерживаю безоговорочно, однако, на мой взгляд, все они заслуживают внимания.
Ещё одна книга того же автора. Как и предыдущая, она скурпулёзно проработана автором и ещё до публикации весьма тщательно обсуждалась в переписке между нами.
С разрешения автора Вы можете бесплатно скачать с сайта полную версию этой книги в формате pdf (файл mechanics.pdf, 3209630 байт). Как и в предыдущем случае, не по всем пунктам мы нашли консенсус, но я считаю, что книга безусловно заслуживает внимания. Ниже я хочу изложить свою точку зрения на те моменты, по которым мы не пришли к согласию.
О центробежной силе при свободном движении
В главе 2 на с.11 сказано: «В момент перехода точечной массы с одной плоскости на другую и начале движения по криволинейной траектории, возникает центробежная сила инерции, направленная по нормали к касательной к криволинейной траектории, причем рассматриваемая точка перехода будет являться вершиной параболы.» Однако движение в рассматриваемой плоскости там свободное и центробежной силы не возникает. Центробежная сила возникает там, где скорость по одной координате (скажем, X), увеличивается за счёт перепендикулярной компоненты скорости (скажем по координате Y), то есть, одна составляющая скорости растёт за счёт другой — Vx за счёт Vy и наоборот, что и происходит при вращении по окружности. Сама центробежная сила здесь только меняет направление движения, но не меняет его количество, и потому работы не совершает (это верно при отсутствии внешней ускоряющей силы). В нашем же случае ускоряющая сила (сила тяжести) действует строго вдоль оси X, её составляющая вдоль оси Y равна нулю, и если бы присутствовала центробежная сила, она бы приводила к изменению компоненты скорости Vy в пользу (с уменьшением) или за счёт (с увеличением) компоненты Vx. Однако компонента Vy стабильна, как показано страницей выше в формулах для компонент Vx и Vy (к сожалению, формул много, но они не пронумерованы, поэтому трудно точно и кратко сослаться на конкретную формулу).
Таким образом, центробежной силы здесь нет, как нет центробежной силы в космическом аппарате, свободно движущемся по вытянутой эллиптической орбите (некоторые участки которой весьма схожи с приведённым примером). В таком аппарате царит невесомость, что является наглядным доказательством отсутствия центробежной силы, а сам этот аппарат по сути находится в «бесконечном свободном падении». Ещё раз подчеркну — центробежная сила обязательно приводит к изменению одной компоненты скорости за счёт другой, именно в этом и заключается её суть, а в нашем случае компонента, перпендикулярная воздействующей силе, не меняется! А раз центробежной силы нет, то и отношение к рассуждениям, построенным на её наличии, соответствующее.
Действительно, «центробежная сила инерции проявляется только в те моменты, когда тело вынуждают изменить траекторию, т.е. вынуждают двигаться по траектории, отличной от траектории свободного движения под действием движущей силы», и при выборе в качестве системы отсчёта плоскости зелёного склона (кстати, абсолютно грамотный выбор) как раз очевидно, что мы имеем случай «свободного движения под действием движущей силы» — как раз из-за неизменности перепендикулярной уклону компоненты скорости. Имеется видимое угловое ускорение, связанное с кривизной траектории, но оно именно видимое, фиктивное, так как нет сил, действующих вдоль оси Y.
О маятнике и тележке
Теперь о второй части книги, где рассматривается идея, представленная в опубликованном на сайте фрагменте.
При обосновании работоспособности «маятника с поршнем» автор исходит из принципа баланса энергий. На мой взгляд, здесь есть ошибка, и заключается она в том, что формула баланса энергий верна для инерциальной системы отсчёта, внешней и неподвижной относительно точки подвеса. Но в инерциальных системах отсчёта центробежная сила (как и сила Кориолиса), являющаяся главным обоснованием работоспособности конструкции, отсутствует в принципе! Там есть лишь силы инерции и силы реакции опоры (подвеса). Центробежная сила и сила Кориолиса существуют лишь во вращающихся неинерциальных системах отсчёта, но там по-другому ведёт себя, например, сила тяжести — по мере движения маятника по своей траектории, в неинерциальной системе отсчёта, связанной с маятником, сила тяжести всё время меняет своё направление, зато сила реакции подвеса как бы не учитывается — её как раз заменяет центробежная сила! Первым правилом физических расчётов является неизменность выбранной системы отсчёта — уж либо инерциальная, либо неинерциальная! Произвольное объединение результатов, полученных в разных системах отсчёта, порождает ложные надежды.
Рассмотрим рисунок слева. На нём красной линией показана траектория плавного перемещения груза. Зелёная и голубая кривые являются четвертями окружности — нисходящей и восходящей ветвями траектории маятника с неизменным радиусом движения. Предположим, что груз (поршень) всю нисходящую ветвь стоит на фиксаторе, который открывается лишь в самом низу, в результате чего поршень быстро перемещается вниз на высоту H и совершает полезную работу (оранжевая стрелка), практически мгновенно относительно периода качания. Затем маятник выходит на горизонтальный участок (его сверхлёгкий и потому безынерционный подвес начинает двигаться по рельсам) и на этом участке под воздействием пружины груз возвращается в прежнее положение (салатовая линия), а затем подвес останавливается и по голубой линии всё возвращается обратно. Если же такого возвращения груза не происходит, то очевидно, что как при сохранении радиуса качания (синяя линия, перемещение точки подвеса синхронно с грузом), так и при сохранении центра качания (увеличении радиуса, чёрная линия) кинетической энергии в нижней точке траектории не хватит для достижения прежней высоты, поскольку работа, совершённая на оранжевом участке, никак не влияет на кинетическую составляющую энергии качания. Поэтому вариант возвращения груза на исходную позицию в любой точке, кроме самой нижней части траектории заранее обречён на неуспех — он просто не поднимется на исходную высоту.
Однако... И вариант траектории «зелёная-оранжевая-салатовая-голубая» принципиально невозможен! Дело в том, что центробежная сила недаром считается «виртуальной», вторичной. Она существует только тогда, когда существует реакция опоры. А как только реакция опоры исчезает (фиксатор освобождается), исчезает и центробежная сила, и проявляется её истинная суть — инерция. Так что при отключении фиксатора в нижней части траектории резкого скачка груза-поршня не получится — он начнёт свободное (по нормали) движение, движение по инерции, т.е. по касательной к траектории в точке освобождения, как камень из пращи.
То есть перемещение груза по оранжевой стрелке невозможно, и в самом «резком» случае оно возможно лишь по касательной жёлтой линии. Итак, наилучшая возможная в реальности траектория — это «зелёный-жёлтый-салатовый-голубой». Замечу, что при этом не предполагается никакое совершение грузом полезной работы. Если же отбирать у груза полезную работу, то его отклонение от круговой траектории будет более медленным, и, соответственно, начинать своё движение он должен намного раньше, а его траектория уже будет не прямой, а параболической. Нисходящая красная ветвь примерно соответствует траектории, по которой должен двигаться груз (поршень), чтобы совершить максимальную полезную работу на участке спуска. То есть наиболее реальной рабочей траекторией является «красный-салатовый-голубой», хотя в реальности груз начнёт радиальное движение не с самого начала, а когда сумма радиальной составляющей силы тяжести и центробежной силы превысит некоторый «порог страгивания».
И тут мы видим следующее. Центробежная сила воздействует на груз тогда, когда вертикальная компонента скорости, получаемая за счёт силы тяжести, благодаря реакции опоры (подвеса) трансформируется в горизонтальную, плавно изменяя общее направление скорости, хотя при этом скорость сама по себе не меняет своей абсолютной величины. Однако радиальное движение имеет свою ненулевую скорость, и на всём нисходящем участке горизонтальная составляющая этой скорости направлена против горизонтальной составляющей качка и всегда перпендикулярно тангенциальной скорости груза, то есть не меняет её. Исключение составляет лишь самая нижняя точка, где радиальная скорость перпендикулярна горизонтальной скорости груза, в свою очередь, в этом месте совпадающей с его тангенциальной скоростью. Таким образом, горизонтальная составляющая скорости груза на всём протяжении параболической нисходящей ветви меньше, чем при движении по круговой траектории, то есть в этом случае груз по горизонтали движется медленнее, чем если бы он двигался по круговой траектории с неизменным радиусом. А стало быть, его кинетическая энергия в нижней точке, которая в этот момент целиком определяется именно горизонтальной составляющей, меньше, и он не сможет набрать прежнюю высоту. Если бы отбора энергии, замедляющего радиальное движение, не было, вертикальная составляющая, добавляемая центробежной силой, компенсировала бы наблюдаемую нехватку горизонтальной составляющей, трансформировавшись в неё за счёт закругляющей движение реакции опоры, но в результате радиального торможения она тоже уменьшается.
Сказанное можно проиллюстрировать на примере жёлтой линии, предпалагающей свободное движение груза от момента начала этой линии. Очевидно, что в этот момент горизонтальная составляющая его скорости меньше, чем она была бы в момент окончания зелёной линии, когда закругление траектории трансформировало бы всю вертикальную составляющую скорости в горизонтальную (безотносительно того, действует на этом участке сила тяжести или нет, в случае если предположить отсутствие силы тяжести, всё особенно очевидно, хотя в любом случае на этом отрезке нет причин для изменения горизонтальной компоненты скорости).
О роли гравитации
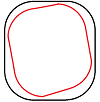
Кстати, продолжая анализ, можно прийти к выводу, что как и в большинстве других «гравитационных» конструкций собственно гравитация здесь используется лишь для начального разгона тележки (и тормозит её при подъёме, что вредно для нас), а всю работу предполагается совершать за счёт инерционных (центробежных) сил и сил упругости пружины. Но придать начальную скорость тележке можно и без гравитации, то есть сама по себе гравитация здесь совсем необязательна. Поэтому выносим всё в невесомость и делаем замкнутый путь со скруглёнными (для сжатия пружины под действием центробежной силы) и прямыми (для распрямления пружины) участками. На рисунке справа чёрная линия показывает путь тележки (рельсы), а красная — схему движения центра масс груза. Чтобы тележка не отрывалась от рельсов, оснастим её магнитом (груз и пружина будут немагнитными) и придадим ей некоторую достаточно большую начальную скорость. Это — квинтэссенция идеи, но тут уже очевидно, что ожидать дальнейшего разгона такой тележжки в невесомости не стоит, даже если для этих целей использовать всю «полезную» работу поршня...
♦
|