Центробежный двигатель
Идея использовать центробежные силы для получения полезного эффекта давно привлекает изобретателей. А силы эти немаленькие и известны людям издавна — ещё библейский Давид убил великана Голиафа камнем, раскрученным в праще! Однако на данный момент это явление как таковое широко используется лишь в двух областях — для нагнетания жидкостей и газов в центробежных насосах и для разделения смесей из компонентов разной плотности в различных центрифугах и циклонах.
Естественно, идея использовать центробежную силу в «замкнутом цикле» посещает и изобретателей вечных двигателей. Вот, например, идея Игоря Высоцкого, использующая в качестве рабочего тела жидкость и опубликованная на его сайте.
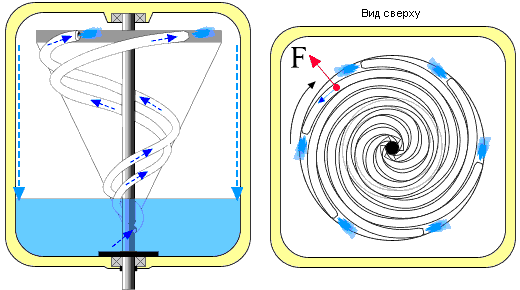 Двигатель Игоря Высоцкого. Буквой F обозначена центробежная сила, ускоряющая жидкость.
Внешне это устройство кажется очень похожим на двигатель Клема в его первом (наиболее распространённом) описании, только у Высоцкого ротор размещён так, что воздействие силы тяжести на любую точку не зависит от его угла поворота. Это, безусловно, более удобно для расчётов, поэтому именно такой вариант и следует взять за основу. Нельзя не отметить и В.Н.Власова, проанализировавшего и оценившего некоторые параметры такого двигателя и высказавшего ряд интересных идей. Именно его анализ и подтолкнул меня серьёзно заняться центробежным двигателем Высоцкого и двигателем Клема. Сразу скажу, результат оказался весьма неожиданным: если двигатель Высоцкого является именно механическим центробежным двигателем и потому не работоспособен, как и другие чисто механические конструкции, то двигатель Клема на самом деле использует совсем другие принципы, и конус со спиралью играет там гораздо более сложную роль, чем простой центробежный нагнетатель рабочего тела (по некоторым сведениям, в двигателе Клема спиральный канал как таковой вообще не являлся одной деталью или её частью, а формировался при сопряжении поверхностей двух деталей, движущихся друг относительно друга).
Спиральный центробежный двигатель
Спираль или «рога»?
Немного истории
Резюме
Спиральный центробежный двигатель
Попробуем разработать и рассчитать конструкцию двигателя Высоцкого с учётом замечаний Власова. Скомпонуем всю спираль (за исключением заборника жидкости) в одной плоскости чуть выше уровня этой жидкости. В результате получился вариант спирали Архимеда, т.е. такой спирали, у которой шаг между витками одинаков по всему радиальному сечению. Допустим, что вся спираль состоит из одной трубки и вращается по часовой стрелке.
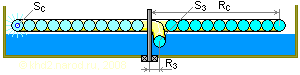 Боковое сечение спирального центробежного двигателя. Rc — радиус колеса (спирали), расстояние от оси вращения до центра сопла; Rз — радиус от оси вращения до центра заборника; Sз — площадь забора жидкости на входе трубки; Sc — площадь сопла на выходе трубки.
Суть замысла такова: скорости вращения должно хватить для того, чтобы поднять захваченную заборником жидкость в основную спираль. Далее под действием центробежных сил жидкость прижимается изнутри к стенке трубы, плавно удаляющейся от центра, и как бы «стекает» по ней к внешнему концу трубки, постепенно набирая энергию вместе с возрастанием линейной скорости более удалённых от центра участков спирали. На внешнем конце спирали она вылетает из сопла с достаточно высокой скоростью, за счёт чего создаёт реактивную тягу, разгоняющую спираль.
Теперь попробуем рассчитать условия перемещения жидкости по трубке под действием центробежных сил с учётом законов гидродинамики. Предположим, что конструкция вращается внешним приводом равномерно с нужной нам скоростью. Предположим также, что внутренний диаметр трубки по всей длине одинаков, за исключением сопла. Гидродинамическим торможением жидкости в трубке пока пренебрежём. В качестве базовой точки отсчёта естественно выбрать ось вращения. Вслед за В.Н.Власовым применим уравнения неразрывности и Бернулли.
Из уравнения неразрывности следует, что расход жидкости в любом сечении трубки, в том числе и в заборнике на её входе, и в выходном сопле, одинаков, то есть
Sз · vз · ρз = Sc · vc · ρc (1),
где S — площадь сечения трубки в выбранном месте, v — скорость потока в этом месте, а ρ — его плотность в рассматриваемом сечении. Поскольку жидкости практически несжимаемы, то если рабочее тело всё время будет оставаться в жидком состоянии, ρз ~ ρс, так что плотности можно будет исключить.
Для того, чтобы реактивная тяга разгоняла спираль, скорость истечения жидкости из сопла должна быть больше линейной скорости этого сопла, иначе за соплом будет создаваться область разрежения, и спираль будет не разгоняться, а тормозиться (хотя и не так быстро, как при полностью заглушенном сопле). Учтём также, что линейная скорость вращающегося тела вычисляется как
v = f · (2 · π · r) (2),
где f — частота вращения (обороты в секунду), r — радиус вращения (здесь и далее маленькой буквой r будем обозначать текущий радиус для рассматриваемого в данный момент участка спирали).
Заменяя линейную скорость угловой (точнее, частотой вращения) и радиусами, получаем Sз · f · 2 · π · Rз = Sc · f · 2 · π · Rc, или, после сокращения подобных членов, Sз · Rз = Sc · Rc. Отсюда для обеспечения разгона спирали при безнапорном заборе неподвижной жидкости следует соотношение размеров входного и выходного отверстий:
Sз / Sc > Rc / Rз (3).
Итак, площадь сопла должна быть как минимум во столько же раз меньше площади заборного отверстия, во сколько раз это сопло находится дальше от оси вращения по сравнению с заборником. Очевидно, что для того, чтобы обеспечить столь высокую скорость истечения жидкости из сопла, существует только одно средство — создать перед соплом достаточно высокое давление. И средства для достижения этого у нас, кажется, есть — это центробежные силы!
Теперь для расчёта давления перейдём к уравнению Бернулли. В нём мы пока пренебрежём гравитационным потенциалом (по сравнению, скажем, с указанной мощностью двигателя Клема — более 300 л.с. (свыше 200 кВт) — поднять жидкость на несколько сантиметров просто пустяк!). Зато в «потенциальном» члене уравнения Бернулли необходимо учитывать действие центробежных сил, которые, кстати, действуют подобно силе гравитации на весь объём жидкости в данном сечении, однако в отличие от ускорения свободного падения, которое вблизи поверхности Земли (± пять-десять километров) практически неизменно, центростремительное ускорение прямо связано с расстоянием до центра вращения, и этим пренебрегать никак нельзя.
Для начала посмотрим, как будет изменяться потенциал центробежных сил в зависимости от радиуса. Поскольку центробежные силы стремятся отбросить жидкость от центра вращения к периферии, наибольший потенциал у жидкости будет возле заборника вблизи оси вращения, а наименьший — у сопла на внешнем краю спирали. Приняв потенциал у сопла за 0, с учётом формулы для центростремительного ускорения мы получим следующую зависимость потенциала от радиуса:
U(r) = Rr∫ aц(x) · dx = Rr∫ (f · 2 · π · x)2 / x · dx = (f · 2 · π)2 · (r – R)2 / 2 = 2 · (f · π · (r – R))2 (4),
где r — радиус вращения рассматриваемого сечения, R = Rc — радиус спирали, равный расстоянию от центра сопла до оси вращения (радиус нулевого потенциала, у оси вращения потенциал максимален), aц — центростремительное ускорение, f — частота вращения спирали вокруг оси.
Итак, в отличие от гравитационного потенциала, который вблизи поверхности Земли изменяется линейно в зависимости от расстояния до точки отсчёта, здесь мы имеем явно выраженную квадратичную зависимость потенциала от радиуса.
Теперь с помощью уравнения Бернулли оценим два крайних случая: давление жидкости возле заглушенного сопла и скорость жидкости относительно спирали при её свободном течении (без трения и изменения сечения — со снятым соплом, — так что разность давлений не возникает).
В первом случае при заполненной спирали мы имеем неподвижную относительно спирали жидкость, поэтому из уравнения Бернулли можно исключить скоростной напор: ρ · Uc + ΔPc = ρ · Uз + ΔPз. Считая Uc = 0 и ΔPз = 0, при заглушенном сопле с учётом формулы (4) мы получаем разность давлений между заборником и соплом равной
ΔP = ρ · Uз = ρ · 2 · (f · π · (Rс – Rз))2 (5).
Что ж, давление можно получить достаточно большое. Например, при R = 20 см и f = 30 об/сек = 1800 об/мин для воды (ρ = 1000 кг / м3) P ~ 7 · 105 Па ~ 7 атм, однако это в отсутствие какого-либо расхода жидкости, и, следовательно, при полном отсутствии реактивной тяги.
Во втором случае мы предполагаем одинаковое давление по всей спирали, поэтому в уравнении Бернулли остаются только потенциал и скоростной напор: ρ · Uc + ρ · vc2 / 2 = ρ · Uз + ρ · vз2 / 2. Считая Uc = 0 и vз = 0 (посчитаем лишь «прибавку» скорости), при свободном течении жидкости с постоянным давлением с учётом формулы (4) после деления на плотность ρ, которая в нашем случае одинакова по всей длине спирали, мы получаем следующее:
Δvc2 / 2 = (f · 2 · π)2 · (Rс – Rз)2 / 2,
откуда следует, что скорость возле сопла превышает скорость возле заборника на
Δv = f · 2 · π · (Rс – Rз) (6).
Поскольку линейная скорость жидкости у заборника относительно спирали vз = f · 2 · π · Rз, добавив её к полученной разности, мы получим, что vс = f · 2 · π · Rс, т.е. равна линейной скорости внешнего конца спирали (2). Это значит, что из внешнего конца спирали жидкость будет выливаться без какой-либо скорости относительно неподвижного резервуара, и в отсутствии трения не будет ни тормозить, ни разгонять спираль. Такой результат замечательно согласуется с интуитивным представлением о том, что сверхтекучая жидкость, захваченная нашей вращающейся спиралью, должна пройти по ней и «выпасть» с другого конца, так и не получив никакой скорости относительно неподвижного резервуара. Кроме того, это косвенно подтверждает правильность наших математических выкладок.
Итак, в предельных случаях мы получаем либо полное отсутствие полезной реактивной тяги (со снятым соплом), либо немалое давление возле сопла при отсутствии какой-либо тяги в принципе (с заглушенным соплом). Попробуем теперь найти «золотую середину» — чтобы сопло не перекрывало поток полностью, но создавало давление, достаточное для достижения нужной скорости истечения струи. Обозначим отношение площади заборника и внутреннего диаметра трубки спирали к площади отверстия сопла Sз / Sс = k. В соответствии с формулой (1) получаем vc = k · vз. Предполагая внутренний диаметр спирали по всей длине до самого сопла одинаковым и равным диаметру заборника, перед входом сопла мы имеем сечение S = Sз и скорость потока vт = vз (vт — это скорость потока жидкости в трубке, и не следует путать её с линейной скоростью самого заборника — это разные вещи). Давление возле сопла повышено относительно атмосферного на входе заборника, однако, если сопло ориентировать строго тангенциально, потенциалы центробежных сил с обоих сторон сопла можно считать одинаковыми и равными 0 (ведь именно сопло мы ранее выбрали в качестве точки отсчёта потенциала). Кстати, такая ориентация сопла является технически оптимальной, поскольку вся реактивная тяга будет направлена именно на раскрутку спирали. С другой стороны, в заборнике давление равно атмосферному, зато имеется максимальный потенциал, рассчитываемый по формуле (4). На выходе сопла сечением Sc = Sз / k вследствие уравнения непрерывности (точнее, закона сохранения расхода) мы имеем скорость vc = vт · k при атмосферном давлении и нулевом потенциале. Наша цель — найти зависимость возможной скорости течения рабочего тела в трубке спирали от её радиуса и скорости вращения и соотношения диаметров трубки (заборника) и сопла.
Составляем соотношение на основе уравнения Бернулли для выхода сопла и входа заборника:
Pатм + ρ · vс2 / 2 = ρ · Uз + Pатм + ρ · vт2 / 2,
сократив подобные члены (атмосферное давление), поделив всё на плотность (которая для жидкости является величиной практически неизменной), получаем
(k · vт)2 / 2 = Uз + vт2 / 2.
Переносим скорости в одну часть уравнения и, умножая обе части на 2, получаем
(k · vт)2 – vт2 = 2 · Uз.
Теперь выносим квадрат скорости за скобки и заменяем потенциал на формулу ( 4): vт2 · (k2 – 1) = (f · 2 · π · (Rт – Rс))2,
откуда вычисляем скорость потока внутри трубки
vт2 = (2 · π · f · (Rз – Rс))2 / (k2 – 1) (7).
Кстати, если давление на входе спирали будет превышать давление на выходе сопла на ΔP (жидкость подаётся в спираль под давлением), то формула примет следующий вид:
vт2 = ((2 · π · f · (Rз – Rс))2 + 2 · ΔP / ρ) / (k2 – 1) (8).
Что следует из полученной формулы?
- Действительные значения решение полученного уравнения имеет только при соблюдении условия k = Sз / Sс > 1, что полностью согласуется с условием (3), поскольку сопло отстоит от центра вращения дальше, чем заборник. Так что эффектный вывод В.Н.Власова о необходимости соотношения Sз < Sс представляется ошибочным!
-
Скорость жидкости внутри трубки спирали и линейно связанная с ней скорость на выходе сопла находятся в линейной зависимости от частоты вращения и размеров спирали. При этом формула не содержит ограничений на соотношение отверстий заборника и сопла, а стало быть, сделав сопло достаточно маленьким, можно получить скорость истечения струи, превышающую линейную скорость сопла, и обеспечить выполнение условия (3), добившись необходимой реактивной тяги!
-
Плотность жидкости не влияет на эффективность работы конструкции (правда, мы пренебрегли сопротивлением воздуха, если же учесть этот фактор, то чем тяжелее жидкость, тем лучше)!
-
Из геометрических параметров в формуле присутствуют только соотношение отверстий заборника и сопла и радиусы, на которых они расположены относительно общей оси вращения. А из этого следует, что многовитковая спираль вроде бы и не нужна — вполне работоспособной должна быть и следующая конструкция (разве что радиус изгиба трубок возле сопел можно сделать побольше для уменьшения потерь на поворот жидкости перед соплом).
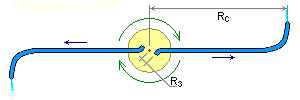 Минимальный вариант двигателя (вид сверху). Показаны две идентичные ветви для обеспечения балансировки колеса. Rc — расстояние от оси вращения до центра сопла; Rз — радиус от оси вращения до центра заборника.
Получается, что «вечный двигатель» у нас в кармане, причём даже не надо вить спираль, а достаточно прикрепить к оси пару трубок?
Проверим формулу (7) на крайние условия: когда k → ∞ (т.е. сопло практически закрыто), скорость рабочего тела в спирали стремится к нулю. Это и понятно — в закрытое сопло жидкость не потечёт. Но вот когда k → 1, то есть площадь сопла становится близкой к площади заборника, скорость начинает стремиться к бесконечности. Расчёт специально приведён подробно и ошибок в нём я не нашёл. Это говорит о том, что слепо использовать полученную формулу нельзя, а надо понять её физический смысл и, стало быть, границы применимости. Дело в том, что vТ — это возможная максимальная скорость идеальной жидкости (без трения) относительно спирали при отсутствии дополнительного давления на входе. Кроме того, необходимо напомнить, что жидкость рассматривалась как идеальная несжимаемая, неиспаряемая и сверхтекучая — без трения и без кавитационных эффектов. Поэтому, когда диаметр сопла равен диаметру трубки, никаких препятствий сверхтекучей жидкости нет, и её скорость теоретически может быть бесконечно большой. Если же сопло начинает уменьшаться, то оно будет ограничивать максимальную скорость даже для сверхтекучей жидкости.
Что ж, попробуем посчитать в конкретных цифрах. Итак, предположим Rз = 2 см = 0.02 м, Sз = 2 см2 = 2 · 10–4 м2 (соответствует «водопроводному» стандарту 1/2"). Рассчитаем по формуле (7) значения vт для нескольких значений радиуса сопла Rс и скорости вращения f. Площадь сопла Sс при этом будем выбирать так, чтобы соотношение сечений k = Sз / Sс примерно вдвое превосходило соотношение радиусов Rс / Rз с тем, чтобы скорость струи из сопла во столько же раз превышала его линейную скорость для создания реактивной тяги.
Таблица 1. Расчёт скорости потока для различных параметров вращения
Скорость вращения спирали
f |
Радиус вращения сопла
RС |
Площадь сопла
SС |
Линейная скорость заборника
vЗ |
Расчётная скорость потока в трубке
vТ |
Расчётная скорость в сопле
vС |
Линейная скорость сопла
v |
| 25 об/сек = 1500 об/мин |
10 см = 10–2 м |
0.2 см2 = 2·10–5 м2 |
3.14 м/с |
1.26 м/с |
12.6 м/с |
15.7 м/с |
| 50 об/сек = 3000 об/мин |
10 см = 10–2 м |
0.2 см2 = 2·10–5 м2 |
6.28 м/с |
2.53 м/с |
25.3 м/с |
31.4 м/с |
| 25 об/сек = 1500 об/мин |
20 см = 10–2 м |
0.2 см2 = 2·10–5 м2 |
3.14 м/с |
2.84 м/с |
28.4 м/с |
31.4 м/с |
| 25 об/сек = 1500 об/мин |
20 см = 10–2 м |
0.1 см2 = 10–5 м2 |
3.14 м/с |
1.42 м/с |
28.3 м/с |
31.4 м/с |
| 50 об/сек = 3000 об/мин |
20 см = 10–2 м |
0.2 см2 = 2·10–5 м2 |
6.28 м/с |
5.68 м/с |
56.8 м/с |
62.8 м/с |
| 50 об/сек = 3000 об/мин |
20 см = 10–2 м |
0.1 см2 = 10–5 м2 |
6.28 м/с |
2.83 м/с |
56.6 м/с |
62.8 м/с |
| 25 об/сек = 1500 об/мин |
50 см = 10–2 м |
0.1 см2 = 10–5 м2 |
3.14 м/с |
3.77 м/с |
75.5 м/с |
78.5 м/с |
| 25 об/сек = 1500 об/мин |
50 см = 10–2 м |
0.025 см2 = 2.5·10–6 м2 |
3.14 м/с |
0.94 м/с |
75.4 м/с |
78.5 м/с |
| 50 об/сек = 3000 об/мин |
50 см = 10–2 м |
0.1 см2 = 10–5 м2 |
6.28 м/с |
7.54 м/с |
151 м/с |
157 м/с |
| 50 об/сек = 3000 об/мин |
50 см = 10–2 м |
0.025 см2 = 2.5·10–6 м2 |
6.28 м/с |
1.89 м/с |
151 м/с |
157 м/с |
Увы, результаты неутешительны — повышение скорости вращения и диаметра спирали лишь приближает скорость истечения струи из сопла к его линейной скорости, но не может достичь её. Попытка же уменьшить диаметр сопла увеличивает скорость струи из него по отношению к потоку в трубке, но сам поток при этом замедляется так, что выигрыша в соотношении скоростей сопла и выбрасываемой струи опять не получается! Математический эффект может дать приближение диаметра сопла к диаметру трубки (наверное, именно это ввело В.Н.Власова в заблуждение относительно соотношения площадей отверстий), но физического смысла это не имеет — ведь ранее мы уже убедились, что если даже сопло будет вообще снято, реактивной тяги мы не получим! Означает ли это, что получить энергию таким образом нельзя? Без изменения фазового состояния тела — да, означает. Но, прежде чем заняться изменением фазового состояния, необходимо уточнить геометрию устройства.
Спираль или «рога»?
Глядя на формулу (7), мы упростили конструкцию, заменив спираль своеобразными загнутыми «рогами». Однако правильно ли это? Давайте рассмотрим оба варианта с точки зрения механики, заменив жидкость твёрдыми тяжёлыми шариками, скажем, стальными, катящимися по стальной трубке в вакууме (чтобы ничто не тормозило их движение, — ведь трение качения стали по стали очень мало).
 Вариант с твёрдыми шарами (одна ветвь, вид сверху).
Под действием центробежных сил шарик сначала будет набирать нормальную (т.е. перпендикулярную к направлению вращения) скорость, а в закругляющемся конце «рога» передавать её ротору, меняя своё направление движения с нормального на тангенциальное, и затем «выпадать» из трубки наружу. Замечательный «вечный двигатель»! Но... Пока шарик двигается по нормали, он, по сути, набирает свою скорость за счёт вращения трубки, по которой он движется, т.е. преобразует тангенциальную скорость того участка трубки, по которому он катится, в свою нормальную скорость, отбирая на этом этапе кинетическую энергию ротора. Если посмотреть на него с точки зрения неподвижной оси вращения ротора, мы увидим, что шарик начинает двигаться не только от центра к периферии, но и вокруг оси вращения вместе с ротором, причём по мере удаления от центра вращения ротора его тангенциальная скорость нарастает, соответствуя тангенциальной скорости проходимого им участка трубки, которая прямо пропорциональна расстоянию до центра вращения. Передавая на завершающем участке траектории свою энергию стенкам трубки, а через неё — ротору, он лишь возвращает эту накопленную энергию обратно. Так что реально никакой прибавки энергии, а значит ускорения и возможности получить дополнительную работу, здесь нет.
Если же вместо перпендикулярного «рога» шарик окажется в спирали, его тангенциальное ускорение не будет столь неотвратимым — он покатится внутри спирали, потихоньку смещаясь к её краю. Поэтому он не сможет отобрать у ротора так много энергии, но и передаст спирали также немного. Так что конечный результат будет таким же, как и в первом случае: при полном отсутствии трения шарик не наберёт тангенциальной скорости и просто «выпадет» из внешнего конца спирали, но часть энергии спирали (весьма малая) будет израсходована на то, чтобы придать шарику небольшую (по сравнению со скоростью шарика относительно самой спирали) нормальную скорость, перемещая его от центра вращения к периферии. Глядя от оси вращения ротора, мы увидим, что шарик не будет вращаться вокруг этой оси, а просто начнёт смещаться к периферии, чем-то напоминая звукоснимающую головку на граммофонной пластинке.
Немного истории
На самом деле и «рога», и плоская спираль не являются последним словом техники. Оба варианта конструкции известны уже не одну сотню лет и нередко использовались в качестве забавных фонтанов. Подобное устройство под названием «эолипил» ещё в античной Греции построил «отец механики» Герон Александрийский (II в. до н.э.). Однако эолипил работал на пару. А в 1750 г. его гидравлический вариант изобрёл венгерский учёный Янош Сегнер, поэтому сейчас такую конструкцию называют «сегнеровым колесом».
И хотя за прошедшие века сегнеровы колёса создавали во множестве различных вариантов со всевозможными сочетаниями параметров (радиусы выхода жидкости и давление на входе, продольные и поперечные профили и сечения канала, число витков спирали и форма «рогов», скорость вращения и расход жидкости и пр.), никаких хоть сколько-нибудь достоверных сведений о проявлении в них «сверхъединичных» эффектов нет. Более того, сверхъединичных эффектов не наблюдается и в наиболее энергоэффективном варианте — при подаче в сопло перегретой жидкости, которая превращается в пар непосредственно во время расширения в сопле, как это происходит в реактивной гидропаровой турбине Зысина.
Резюме
Подводя общий итог, можно сказать, что механический центробежный «вечный двигатель» без изменения фазовых состояний рабочего тела или каких-то других немеханических способов получения дополнительной энергии невозможен в принципе — это лишь перераспределение энергии между отдельными элементами внутри системы без её увеличения или извлечения из окружающей среды, зато с неизбежными в реальном мире потерями на трение и рассеяние.
♦
|