Вихревое движение жидкостей и газов

Вихревое движение идеального газа
   Поворот потока идеального газа
      Сжатие и расширение потока газа при повороте
      Разделение частиц потока по скоростям
   Завихрение идеального газа по 2 осям
Турбулентность и сложное вихревое движение

Вихревое движение идеального газа

Для начала постараемся не изобретать велосипед, а рассмотрим термодинамические эффекты вихревого движения с точки зрения классической термодинамики, прежде всего на примере знакомого со школы идеального газа, то есть такого газа, в котором взаимодействие его частиц — атомов или молекул — между собой хорошо описываются моделью их идеально упругих соударений, а прочие эффекты этого взаимодействия пренебрежимо малы по сравнению с их взаимодействием с стенками сосуда, в котором этот газ находится. На практике это означает прежде всего пренебрежение вязкостью газа и электрическими явлениями, возникающими при быстром движении потоков реальных газов.

Поворот потока идеального газа

Как известно, температура и давление идеального газа изменяются при изменении плотности и скорости его частиц, и наоборот. Посмотрим, что может произойти, если однородный поток такого газа, движущийся с достаточно большой скоростью, вдруг будет вынужден повернуть из-за плавно закругляющейся стенки сосуда. При этом попробуем оставаться на самых примитивных механистических позициях, соответствующих представлениям об идеальном газе как о множестве идеально упругих шариков, только очень маленьких и лёгких...

Предположим, что ламинарный (без завихрений) поток идеального газа подаётся на вход трубы прямоугольного (для простоты) сечения, которая представляет собой сегмент окружности (скажем, половину, т.е. плавно поворачивает на 180°).

Сжатие и расширение потока газа при повороте

В соответствии с механической моделью газа частицы-шарики должны стремиться продолжить начальное прямолинейное движение, однако на их пути оказывается плавно закругляющаяся внешняя стенка. В результате возле неё возрастает концентрация частиц, т.е. происходит некоторое уплотнение газа, что в соответствии с рассмотренным выше адиабатическим сжатием ведёт к повышению температуры и давления в этой области. У внутренней же стенки трубы, наоборот, возникает разрежение газа — это соответствует адиабатическому расширению и ведёт к уменьшению там давления и температуры. В отличие от металлических шариков, которые непременно скопились бы у внешней стенки трубы все сразу, в газе слишком много частиц, и каждая из них помимо направленного движения вместе с потоком имеет хаотическую тепловую компоненту движения. Поэтому в результате их взаимных столкновений многие из них так и не достигают внешней стенки, а меняют своё направление полёта намного раньше, ведь длина свободного пробега частиц воздуха при атмосферном давлении исчисляется сотыми долями микрометра. В результате весь газ не скапливается у внешней стенки, а у внутренней стенки не образуется абсолютного вакуума, однако разность давлений и температур тем выше, чем выше направленная скорость потока на входе трубы.

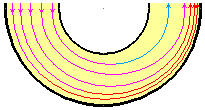Схема изменения плотности потока газа при повороте в трубе. Плотность линий соответствует плотности газа (т.е. его давлению), а цвет — температуре.

Впрочем, следует отметить, что такое разделение имеет место только во время поворота потока. Если при выходе на прямой участок (или за пределы трубы) давление в обоих частях потока сравняется (в сжатой — уменьшится, в разреженной — увеличится), то разность температур, вызванная этим, пропадёт, даже когда потоки останутся отделёнными друг от друга. Однако, пока газ находится в трубе, можно снять тепло с её внешней стенки или холод — с середины трубы. Следует заметить, что речь идёт об изменении именно внутренней тепловой энергии самого газа, а не об отборе механической энергии, переданной газу нагнетателем при создании потока.

Разделение частиц потока по скоростям

Существует и второй аспект, приводящий к аналогичным результатам. По общепринятым термодинамическим представлениям, частицы газа и жидкости обладают существенной тепловой кинетической энергией, причиной которой является их хаотическое тепловое движение. Очевидно, что у некоторых из них эта тепловая скорость складывается с макроскопической скоростью потока, и в результате их скорость (а следовательно, и кинетическая энергия) относительно трубы возрастает, а у некоторых эти скорости вычитаются, в результате их скорость относительно трубы становится меньше, а то и вовсе направлена в противоположную сторону. Выбор трубы в качестве точки отсчёта здесь абсолютно однозначен — ведь она отклоняет поток от прямолинейной траектории, и, привязавшись к потоку, мы получим неинерциальную систему отсчёта, а неподвижной является именно направляющая труба. Даже интуитивно понятно, что «низкоскоростным» частицам завернуть легче, чем «высокоскоростным», в результате автоматически происходит их разделение — имеющие более высокую скорость (а стало быть, энергию и температуру) концентрируются у внешней стенки трубы, а обладающие более низкой скоростью и энергией остаются в её внутренней части. Благодаря этому также происходит разделение температур внутреннего и внешнего слоёв потока. Это наиболее очевидно в случае, когда длина свободного пробега частиц много больше внутренних размеров направляющей трубы (разреженный газ), однако эффект, хотя и в менее выраженной форме, будет иметь место и в случае, если свободный пробег существенно меньше этих размеров (газы при атмосферном давлении) и даже когда такой пробег практически отсутствует (различные жидкости) — за счёт передачи импульсов при взаимных столкновениях частиц.

Это разделение более устойчиво — оно в значительной степени сохраняет свои свойства и после выхода на прямой участок и выравнивания давлений «холодной» и «горячей» частей потока (при условии предотвращения их смешивания). Результатом такого эффекта, как и для предыдущего пункта, будет эффект Ранка.

Завихрение идеального газа по 2 осям

Говоря об эффекте Ранка, мы рассматривали вращение потока вокруг одной оси. Но если струя закрученного потока, в свою очередь, будет завиваться вокруг другой оси, перпендикулярной первой? А ведь именно так ведут себя практически все природные вихри — от разрушительного торнадо до безобидной воронки в ванной, из которой выпускают воду. Как правило, у всех у них основной вихрь состоит из закрученных потоков-струй, каждая из которых вращается вокруг своей оси. Возможно, это неслучайно, и сама природа подсказывает нам не ограничиваться вращением в одной плоскости?

Предположим, что нам каким-либо образом удалось создать статический тороидальный вихрь, то есть вихрь, имеющий форму трубки, замкнутой в кольцо, в котором рабочее тело (газ или жидкость) вращается вокруг оси этой трубки, но не вращается вокруг оси самого кольца.

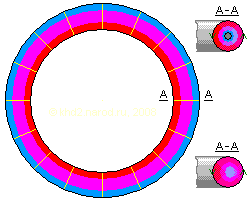Тороидальный статический вихрь. Цвет соответствует температуре. Разрез вихревой трубки A—A показан для двух случаев: вверху — с вращением, центрированным благодаря жёсткому сердечнику, внизу — из-за отсутствия жёсткого сердечника центр вращения смещён к периферии и температурные эффекты выражены слабее.

Если разбить такое кольцо на сектора, то станет очевидно, что сечение у внутренней стенки трубки (к центру кольца) меньше, чем у внешней (на периферии кольца). Соответственно, рабочее тело будет испытывать ближе к центру кольца сжатие и адиабатический нагрев, а у периферийной стенки — расширение и адиабатическое охлаждение, кроме того в соответствии с уравнением непрерывности у центральной стенки рабочее тело будет двигаться быстрее, а у периферийной — медленнее. Первый эффект более выражен для газов, второй — для жидкостей. И тот, и другой эффекты вызовут более высокую температуру у внутренней стенки вихревой трубки и более низкую — у периферийной. Каждый цикл вращения перенесёт лишь немного энергии, но он повторяется быстро и очень много раз, что в сумме может привести к вполне заметной разности температур. Впрочем, при отсутствии жёсткого сердечника внутри трубки центр вращения несколько сместится к периферии, что значительно снизит перенос тепла, да и без жёсткой внешней трубки такой вихрь долго не просуществует. Эффект Ранка здесь, конечно, также имеет место, однако в данном случае его влияние представляется непринципиальным, особенно при не слишком высоких скоростях вращения.

В случае, если подобный вихрь будет вращаться ещё и вокруг центра кольца, траектория движения отдельной частицы превратится в спираль, свитую более или менее туго в зависимости от соотношения скоростей вращения вокруг центра вихревой трубки и вокруг центра кольца. При этом перенос тепла возможен как от периферии кольца к его центру (при незначительной скорости вращения вокруг центра кольца), так и от центра кольца к его периферии вследствие эффекта Ранка (при незначительной скорости вращения вокруг центра трубки).

Турбулентность и сложное вихревое движение

Традиционная гидродинамика неявно исходит из того постулата, что естественной формой движения жидкостей и газов является ламинарное течение, а турбулентность рассматривается как его нарушение, вызванное тем или иным ограничением его «свободы». Однако, исходя из того факта, что течение, бывшее ламинарным в относительно узком канале, при удалении ограничивающих его стенок и сохранении прежней скорости начинает завихряться, логично заключить, что именно вихревое течение является «естественной» формой движения жидкостей и газов, а ламинарным оно становится вынужденно — как раз под воздействием внешних ограничений! Достаточно взглянуть на формулу числа Рейнольдса — общепризнанного критерия ламинарности или турбулентности потока, — при неизменной скорости потока оно растёт пропорционально диаметру трубы, а значит, течение становится более турбулентным. В узкой трубке мчащаяся с большой скоростью жидкость ламинарна, а в безбрежном океане даже медленные течения сопровождаются водоворотами и завихрениями — такими же медленными, малозаметными и безопасными, как и породивишие их потоки.

Вихрь вытекающей воды. Явно видна его чёткая структура.

Что из этого следует? Очень многое! Как известно, будучи предоставлено само себе, любое тело или вещество стремится принять наиболее энергетически выгодное состояние и перемещается по наиболее энергетически выгодной траектории. А значит, получается, что естественное турбулентное завихрённое течение энергетически более выгодно, чем прямолинейное ламинарное? Но ведь традиционная гидродинамика, да и реальная техническая практика утверждают: потери при ламинарном движении существенно меньше, чем при турбулентном, и потому инженеры всеми силами стараются предотвратить или хотя бы сократить образование турбулентностей! В чём же дело?

В массовом сознании турбулентное движение ассоциируется с беспорядочно зарождающимися и исчезающими вихрями среды, которые хаотично сталкиваются друг с другом, а также с ограничивающими поток стенками или с телом, движущимся в неограниченной среде, и тем самым отбирают и бесполезно растрачивают кинетическую энергию, превращая её в тепло. Да, иногда это выглядит именно так, однако происходит не очень часто и обычно в тех случаях, когда форма движущегося тела или стенок, ограничивающих поток, слишком неправильна, а жёсткость их поверхности мала. Следует заметить, что в быту и технике под «турбулентностью» часто имеется в виду именно такое хаотичное завихрение среды, однако в гидродинакмике как науке «турбулентным» называется любое течение, характер которого отличен от ламинарного, то есть с любыми завихрениями в теле потока — как хаотическими, так и упорядоченными — вплоть до квазистационарных.

Тем не менее, легко получить квазистационарную струю, которая хотя и имеет форму спирали (т.е. является турбулентной с точки зрения гидродинамики), но внешне выглядит практически неподвижной. Для этого достаточно под небольшим давлением (в пределах 0.1..0.5 атм) подать жидкость в небольшое отверстие (1..3 мм), желательно продолговатой формы. Это может быть не только вода из водопровода, — опыт можно провести за завтраком, наливая в чай или кофе молоко из молочного пакета. В результате при условии неизменного напора в воздухе можно будет наблюдать внешне неподвижную спирально закрученную монолитную струю длиной до 15–30 см (увеличению длины цельного участка способствуют как ровные края отверстия и повышение напора, так и уменьшение размеров отверстия — в разумных пределах, конечно, иначе получится пульверизатор). На большем расстоянии цельная струя разрушается под действием сопротивления воздуха и силы тяжести, разбиваясь на отдельные капли. Опыт легко доступен каждому, и весьма поучительно понаблюдать за поведением струи при небольших изменениях напора. Интересно, какой длины можно получить цельную струю в невесомости и при сильном разрежении?

Проведя такой опыт, можно наглядно убедиться, что турбулентное движение среды весьма упорядоченно, правда, эта упорядоченность динамическая, «живая», зависящая прежде всего от размеров потока (обтекаемого тела) и его скорости, но не только от них — важную роль может играть и изменение вязкости, и шероховатость поверхности, и многие другие факторы. При не очень большом изменении параметров точки наибольшего и наименьшего динамического сопротивления перемещаются по ограничивающей поток поверхности более чем заметно, в том числе и меняясь местами. Да и при неизменных параметрах из-за труднопредсказуемой динамической реакции среды жгуты струй могут двигаться, качаться, — их сложное вращательное движение порождает то нарастание, то уменьшение давления и сопротивления движению в одной и той же точке этой поверхности. В этом трудность детального приборного исследования турбулентных течений. В этом отличие турбулентного движения от достаточно «статического» и потому гораздо лучше изученного ламинарного движения, где при изменении скорости лишь соответственно изменяется давление и сопротивление, но точки минимумов и максимумов сопротивления остаются на своих местах до тех пор, пока сохраняется ламинарный режим. В этом и причина принятой в технике и обслуживающей её науке догмы о вреде турбулентности.

Действительно, если параметры канала не соответствуют «естественной» форме вихря для данных условий, энергетические потери могут превысить потери при ламинарном движении, а даже небольшое изменение условий течения приводит к существенному изменению геометрии оптимального канала. В жёстких каналах, характерных для технических устройств, оптимально подстроить их форму практически невозможно. Не удивительно, что предпочтение отдаётся предсказуемому и легко рассчитываемому ламинарному течению — «синице в руках». Казалось бы, мягкая оболочка канала должна сама подстроиться под оптимальный профиль, но и здесь всё не так просто. Общеизвестно, что как в воздухе, так и в воде мягкая оболочка (тканевая или резиновая) оказывает большее сопротивление движению, чем жёсткая металлическая — именно потому, что она «полощется» в потоке. Здесь дело в том, что она действительно пытается «подстроиться» под оптимальную форму, но изменение формы изменяет и условия обтекания — и новая форма снова оказывается неоптимальной, вызывая обратное движение. То есть, вместо того, чтобы предвосхищать события и заранее принять оптимальную форму, «тряпочная» оболочка стремится «ликвидировать последствия» и потому всегда опаздывает и проигрывает — находится в энергетически неоптимальном состоянии относительно потока, обтекающего её в данный момент.

Конечно, существует и другой вариант — оптимизировать параметры потока (прежде всего скорость) под жёсткий профиль трубы. Однако этот вариант, похоже, никем всерьёз не изучался и не просчитывался, особенно для длинных каналов и трубопроводов. Единственной заслуживающей внимания работой в этом плане являются эмпирические опыты гениального Виктора Шаубергера, однако научного развития и общепринятого теоретического обоснования они не получили, а без этого их инженерное применение невозможно — ведь инженерам нужен предсказуемый и заранее просчитанный результат, особенно в таких долговременных и дорогостоящих проектах, которыми являются трубопроводы и гидротехнические сооружения. Да и профиль труб Шаубергера гораздо сложнее, а потому менее технологичен, чем традиционные круглые трубы. Так зачем рисковать?

Наблюдая много лет за течениями, прежде всего естественным течением горных и равнинных рек и ручьёв и поведением их обитателей, Виктор Шаубергер пришёл к выводам, которые современная общепризнанная гидродинамика не то что отрицает, а просто не считает нужным рассматривать. Физическая суть их заключается в том, что должным образом организовав и направив турбулентное течение, можно не просто сократить потери, но и превратить часть внутренней (тепловой) энергии воды в механическую работу — то есть усилить течение за счёт охлаждения воды. Особое внимание он уделял горной форели, которая, используя особые свойства ледниковой воды и создав канал нужного профиля с помощью рта и жаберных крышек, может долго стоять в стремительном потоке горного ручья на одном месте, почти не работая плавниками и хвостом, а потом ещё и сделать рывок вперёд — против течения!

Более подробно его идеи и разработанные на их основе устройства рассмотрены на отдельных страницах, а здесь я лишь хочу подчеркнуть, что не всегда следует стремиться к подавлению турбулентности — есть ситуации, когда именно правильно организованное сложное турбулентное движение может дать энергетический выигрыш! ♦