Физика. Справочная информация
Это краткий конспект основных понятий, законов и формул по механике, гидравлике, классической термодинамике, электромагнетизму и частично фотометрии, которые мне требуются наиболее часто. Он не претендует на исчерпывающую полноту, хотя и является достаточно полным для того, чтобы я обращался к другим справочникам лишь в довольно редких и частных случаях. По возможности, большинство формул представлены в интегральном виде (так сказать, «школьном», в отличии от «институтского» дифференциального представления). Во-первых, часто этого вполне достаточно для практического использования. Во-вторых, в Интернете и солидных справочниках обычно всё приводится именно в дифференциальном виде, так что найти такой вид для той или иной формулы не проблема. Зато проблемой часто является правильно взять интеграл этой формулы при конкретных вычислениях, особенно для тех, кто изучал матанализ очень давно или не изучал высшую математику вообще и слабо разбирается в дивергенциях, роторах и градиентах. В-третьих, те, кто «чувствует» физику, знают и пределы использования интегральной формы — для установившихся процессов в относительно неизменных условиях, — и обычно им не составляет большого труда в нужный момент перейти к дифференциальной форме для учёта нестационарности того или иного параметра. Тех же, кто физики «не чувствует», в этих случаях не спасёт и дифференциальная запись формул.
Несколько общих замечаний
Размерности физических величин
Скалярные и векторные величины
Скорости и градиенты
Механика
Механические величины
Основные законы механики
Вращение
Направление вращения. Сочетание вращения с поступательным движением
Центробежная сила
Сила Кориолиса
Гироскопические эффекты
Кинетическая энергия вращения. Момент инерции
Основные законы аэро- и гидростатики
Основные законы аэро- и гидродинамиики
Классическая термодинамика
Термодинамические величины
Основные понятия классической термодинамики
Основные законы классической термодинамики
Электромагнетизм
Электрические и магнитные величины
Общее описание электромагнитного взаимодействия
Электростатика
Постоянный электрический ток
Электромагнетизм
Фотоны и электромагнитное излучение
Элементы квантовой механики
Физические константы и стандартные величины
Универсальные физические константы
Стандартные физические величины
Несколько общих замечаний
Размерности физических величин
Все представленные ниже формулы и значения физических величин приведены в международной системе единиц измерения СИ (метр — килограмм — секунда — кельвин — ампер — кандела). Внимание! При расчётах, прежде чем подставить в формулы численные значения, необходимо убедиться, что все они преобразованы именно к СИ. Перевод в систему СИ национальных и неметрических единиц измерения представлен на отдельной странице.
При расчётах по собственным формулам необходимо проверять размерности (т.е. единицы измерения) левой и правой частей — они должны быть одинаковы (стерадианы, радианы, угловые градусы и синусы-косинусы-тангенсы от них, а также проценты, штуки и разы являются безразмерными величинами). В случае возникновения недоразумений (скажем, слева паскали, а справа ньютоны на квадратный метр) проверку размерностей следует выполнять, предварительно приведя все единицы измерения компонентов формулы к основным единицам измерения (указаны мелким шрифтом для тех величин, единицы измерения которых не являются основными). Несовпадение размерностей однозначно говорит о том, что формула ошибочна.
И ещё одно важное замечание. Совпадение размерности (единиц измерения) результата той или иной формулы с размерностью одной из физических величин ещё не означает идентичности их физического смысла! Пример: произведение силы на механическую скорость F · v по своей размерности совпадает с мощностью, но физического смысла мощности как скорости совершения работы или скорости изменения энергии это произведение не имеет (вернее имеет, но в очень узких условиях — когда тело под действием силы набирает или теряет свою механическую скорость полностью, с нуля, причём строго за одну единицу времени, выбранную для расчёта). Другой пример — размерность момента силы, выраженная в основных единицах измерения, совпадает с размерностью работы и энергии, но это совершенно разные физические величины. Наконец, и сами работа и энергия измеряются в одних и тех же единицах — джоулях, — но имеют разные физические смыслы, хотя и тесно связанные между собой, — первое является мерой совершённого воздействия, а второе — мерой возможности совершить такое воздействие. Отождествление физических величин лишь на основе совпадения их размерностей иногда может привести к весьма нетривиальным «открытиям», но эти бумажные «открытия» не будут иметь отношения к реальному миру! Поэтому у названия каждой величины в скобках я специально указал её физический смысл. Каждый термин классической физики неслучаен и отражает своё особое понятие — здесь терминология отточена поколениями учёных отнюдь не последнего разряда...
Скалярные и векторные величины
Физические величины могут быть скалярными и векторными.
К скалярным величинам относятся те, к которым нельзя приложить понятие «направление». В механике это длина, площадь, объём, масса, а также работа, энергия, мощность и время. При объединении однородных скалярных величин обычно просто складываются их значения. Однако многие скалярные величины могут иметь знак, который необходимо учитывать. Так, для работы знак означает направление передачи энергии. Иногда работа, совершаемая самим телом (тело отдаёт энергию) указывается со знаком «минус», а работа, совершаемая над телом (тело получает энергию из среды или от других тел) — со знаком «плюс», но может быть и наоборот. Ещё чаще знак вообще не ставится, а направление передачи указывается словами, например «тело совершило работу» или «тело приобрело энергию», но для расчёта баланса энергии всё равно надо правильно учитывать знаки, — иначе, рассматривая вращение обыкновенного колеса, на бумаге можно легко получить огромный выход «лишней» энергии, хотя в реальности ничего подобного нет! Строго говоря, работу, мощность и энергию (а в некоторых случаях и время) следует рассматривать как вектора в особых одномерных пространствах, представленные «скалярными величинами со знаком», однако обычно в физике «векторными» называют лишь величины, имеющие направление именно в обычном трёхмерном пространстве.
К векторным величинам относятся те, которые имеют определённое направление в пространстве. В механике это перемещение и все производные от него — скорость, ускорение, импульс, сила, давление. При их сложении обязательно нужно учитывать их взаимную ориентацию. Однородные величины, направленные в одну сторону, суммируются, в противоположные — вычитаются, а в общем случае их влияние определяется проекцией на нужное направление.
Векторные величины выделены надчёркиванием над названием и обозначением.
Как правило, величины, зависящие как от векторных, так и от скалярных величин, сами являются векторными и вычисляются как произведение трёхмерного вектора на число. Например, сила зависит от скалярной массы и векторного ускорения и является векторной величиной. Наоборот, если оба сомножителя являются векторами или оба — скалярами, результат обычно скалярный. Так, мощность определяется двумя скалярными величинами — работой (энергией) и временем — и является скалярной величиной. В то же время работа, определяемая двумя векторными величинами — силой и перемещением — считается скалярной величиной и вычисляется как скалярное произведение трёхмерных векторов силы и перемещения. Но есть и исключения — скажем, сила Лоренца или скорость прецессии являются векторными величинами, вычисляемыми как векторное произведение других векторных величин.
Скорости и градиенты
Многие физические величины могут не только изменяться с течением времени, но и быть различными в разных точках пространства в один и тот же момент времени. Прежде всего это относится к потенциалам полей разного рода.
В связи с этим можно говорить о временнóй и пространственной скоростях изменения таких физических величин. В первом случае речь идёт об изменении характеристик одного и того же объекта или точки пространства в разные моменты времени (время меняется, объект или координаты неизменны), во втором случае имеется в виду пространственное изменение характеристик в один и тот же момент времени либо тогда, когда течение времени не имеет значения, то есть поле стационарно (время одно, объекты или координаты разные). В «институтском» курсе физики в этих случаях часто говорят о «временнóм и пространственном градиентах» соответствующей физической величины. Для краткости и однозначности я постараюсь придерживаться следующей системы понятий: «скоростью» я буду называть темп изменения физической величины во времени, а «градиентом» — степень её изменения в пространстве. Таким образом, «скорость изменения высоты» подразумевает механическую скорость взлёта или падения, а «градиент высоты» соответствует уклону, то есть степени изменения высоты некоторой поверхности в пространстве.
Следует заметить, что скорость, как и градиент, имеет смысл лишь при плавном изменении физической величины. Если изменение происходит резко, скачком, то в этот момент скорость становится бесконечно большой, а градиент терпит разрыв. На самом деле в классической физике неизвестны мгновенные процессы. Там даже самый быстрый процесс имеет конечную длительность, а значит конечную (хотя иногда и очень большую) скорость и неразрывный (хотя иногда очень крутой) временнóй градиент. Зато легко привести пример разрыва пространственного градиента, каковым является, скажем, любая кромка поверхности.
Механика
Помимо собственно механики (механического взаимодействия твёрдых тел), здесь приводятся некоторые сведения по аэро- и гидростатике, а также аэро- и гидродинамике.
Механические величины
| Понятие |
Обозначение и формула |
Единица измерения |
|
Расстояние, перемещение, длина (мера размещения тела в пространстве)
|
d, r, s или l |
метр (м) |
|
Площадь (для трёхмерного пространства — мера границы между пространством внутри и вне тела; иногда (площадь проекции) — мера восприятия телом распределённых (не точечных) внешних воздействий)
|
S |
квадратный метр (м2) |
|
Объём (мера пространства, занимаемого телом)
|
V |
кубический метр (м3) |
|
Время (мера причинно-следственных связей между событиями)
|
t |
секунда (с) |
|
Частота (мера скорости повторения процессов)
|
f |
герц (Гц = 1 / с) |
|
Скорость (мера изменения положения в пространстве)
|
v = s / t |
метр в секунду (м / с) |
|
Ускорение (мера изменения скорости)
|
a = Δv / t |
метр в секунду за секунду (м / с2) |
|
Масса (мера механической инертности тел, т.е. инерционности; мера взаимодействия тел с гравитационным полем)
|
m |
килограмм (кг) |
|
Удельная плотность (мера концентрации массы в объёме)
|
ρ = m / V |
килограмм на кубический метр (кг / м3) |
|
Момент инерции (мера способности тела сохранять вращение вокруг определённой оси)
|
J = ∑ (mi · ri2) |
кг · м2 |
|
Импульс (механический — мера количества движения тела)
|
p = m · v |
кг · м / c |
|
Сила (мера воздействия на тело, способного изменить его перемещение в пространстве)
|
F = m · a |
ньютон (Н = кг · м / с2) |
|
Момент силы (мера вращающего действия силы на рычаг, закреплённый на шарнире)
|
M = F · r |
ньютон на метр (Н · м)
|
|
Давление (мера распределения силы по площади, т.е. по поверхности или по сечению тела)
|
P = F / S |
паскаль (Па = Н / м2)
|
|
Работа (мера воздействия на тело, вызывающего изменение его состояния, в механике — вызывающего перемещение под действием силы, внешней или внутренней)
|
A = F · s |
джоуль (Дж = Н · м)
|
|
Энергия (мера способности тела совершить работу)
|
E = A |
джоуль (Дж = Н · м)
|
| Кинетическая энергия |
Eк = m · v2 / 2 |
|
Потенциальная энергия в гравитационном поле
|
Eп = m · g · Δh, где g — ускорение свободного падения, Δh — разность высот, между которыми переместилось тело массой m.
|
|
Мощность (мера скорости совершения работы, а также мера скорости расхода или поступления энергии)
|
W = A / t = ΔE / t |
ватт (Вт = Дж / с)
|
Основные законы механики
Закон относительности движения: при равномерном прямолинейном движении тел, на которые нет внешних воздействий, невозможно выбрать абсолютную точку отсчёта и неоспоримо определить, какое тело движется, а какое стоит на месте. Система отсчёта, начало которой движется равномерно и прямолинейно, называется инерциальной системой отсчёта. Все инерциальные системы отсчёта равнозначны между собой. Внимание! Это верно лишь пока движущиеся тела не взаимодействуют ни с чем. Закон сохранения энергии в полной мере выполняется лишь в тех инерциальных системах отсчёта, которые неподвижны относительно центра масс всей системы взаимодействующих тел!
Первый закон Ньютона: тело, двигающееся равномерно и прямолинейно, в отсутствие внешних воздействий сохраняет это движение неограничено долго. Это проявление инертности тел.
Второй закон Ньютона в современной формулировке: скорость изменения импульса тела равна действующей на него силе. Отсюда прямо вытекает формула, связывающая силу и ускорение: F = Δp / t = m · Δv / t = m · a, или в дифференциальной форме: F = dp / dt = m · dv / dt = m · a. Оригинальная (ньютоновская) формулировка этого закона: «изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует» (в те времена векторные величины не применялись, а абсолютное значение величины и её направление действия считались отдельными категориями). Таким образом, изменение импульса происходит только под действием приложенной силы и требует энергетических затрат (статическая сила, не изменяющая перемещения объекта приложения, на тело действует, но не меняет ни его импульс, ни энергию). Важное следствие: если объект не меняет скорость, то на него не действуют никакие силы либо их действие взаимно скомпенсировано; поэтому в данном случае обязательно имеется в виду полная векторная сумма всех действующих на тело сил, но ни в коем случае ни часть из них и ни какая-либо из этих сил в отдельности!
Третий закон Ньютона: сила, с которой одно тело действует на другое, численно равна силе, с которой это второе тело действует на первое, но направлена в противоположную сторону (сила действия равна силе противодействия).
Законы Ньютона традиционно преподаются по отдельности, однако они взаимосвязаны, поэтому стоит помнить об объединённой формулировке законов Ньютона: тело всегда противодействует ускоряющей его силе, причём сила противодействия численно равна скорости изменения импульса тела (произведению массы тела на получаемое им ускорение) и направлена строго противоположно ускоряющей силе; если же все ускоряющие силы взаимно скомпенсированы либо их нет, то скорость тела изменяться не будет (оно сохранит равномерное движение или пребывание в относительном покое).
Правило моментов: для идеального рычага, закреплённого на одном шарнире и находящегося в покое, сумма всех моментов силы, приложенных к рычагу относительно шарнира, равна нулю (все моменты взаимно скомпенсированы).
Закон сохранения импульса: при взаимодействии тел общий механический импульс всей системы взаимодействующих тел остаётся постоянной величиной — происходит лишь перераспределение импульса между телами. Этот закон инвариантен (равно справедлив) для любых инерциальных систем отсчёта. Внимание! Имеется в виду сохранение суммарного импульса в одной и той же системе отсчёта; сами же импульсы при переходе к системе отсчёта, движущейся относительно прежней, обязательно изменят свои величины, может измениться и их сумма.
Закон сохранения энергии: при взаимодействии тел общая энергия всей системы взаимодействующих тел остаётся постоянной величиной — происходит лишь перераспределение энергии между телами и преобразование её из потенциальной формы в кинетическую и обратно (в более общем случае возможно преобразование энергии в другие виды, например из механической в электромагнитную или тепловую, однако суммарная энергия системы всё равно не изменяется). Внимание! Закон сохранения механической энергии неинвариантен и в полной мере выполняется лишь в инерциальной системе отсчёта, неподвижной относительно центра масс всей системы взаимодействующих тел! Абсолютные значения энергий тел и их сумма при переходе к системе отсчёта, движущейся относительно прежней, также изменятся.
Закон всемирного тяготения: две материальные точки с массами m1 и m2, находящиеся на расстоянии r друг от друга, взаимно притягиваются с силой F = G · m1 · m2 / r2, где G — гравитационная постоянная.
Закон Гука (сила упругой деформации): F = k · Δl / l = k · δl, где k — коэффициент упругости (для монолитных твёрдых материалов это модуль Юнга, умноженный на площадь сечения, перпендикулярного направлению деформации); l — исходная (без каких-либо нагрузок) длина тела в направлении деформации; Δl — изменение длины под воздействием деформирующей силы от её исходного значения в абсолютном выражении (в метрах, а не в процентах); δl — изменение длины тела относительно отсутствия деформирующей нагрузки (в разах). Перед применением закона Гука следует быть уверенным, что деформация является именно упругой, а не пластической. В реальности зависимость силы от степени деформации при небольших усилиях очень близка к линейной, но всё же никогда не является таковой.
Вращение
Различные виды вращения являются основным видом движения материи в природе.
Свойства вращательного движения кардинально отличаются от равномерного прямолинейного. Равномерное прямолинейное движение относительно. Вращательное движение абсолютно. То есть, находясь практически в любой системе отсчёта, даже неинерциальной, за достаточный период времени можно однозначно определить дугу траектории любого наблюдаемого тела и по ней вычислить центр, радиус и скорость его вращения. Именно это позволяет астрономам с Земли определить параметры движения космических объектов, в том числе скорости и радиусы вращения планет вокруг Солнца.
Направление вращения. Сочетание вращения с поступательным движением
Часто говорят о левом и правом вращении. Однако для плоского вращения его направление относительно — стоит взглянуть с другой стороны, как левое вращение диска будет выглядеть правым, и наоборот. Но как только движение из кругового становится спиральным, то есть как только в дополнение к вращению появляется поступательная составляющая, тут же возникает абсолютная разница между левым и правым вращением — на винт с левой резьбой никак нельзя навернуть правую гайку с теми же параметрами резьбы.
При замыкании поступательной компоненты такого движения в кольцо получается многомерное вращение (замкнутая спираль). Наиболее распространённым физическим примером многомерного вращения является вихрь Бенара — основная форма движения сред в природе. В связи с возникновением новых свойств у многомерного вращения было бы принципиально неверно отождествлять рассматриваемое ниже элементарное вращение твёрдых тел с природными вихревыми процессами. У возникающих в различных средах вихрей появляются новые свойства, нехарактерные для простейшего вращения, в частности длительная устойчивость свободного существования без видимых причин, сдерживающих их распад.
Центробежная сила
Центростремительное ускорение: aц = v2 / R = ω2 · R = (2π · f)2 · R, где v — линейная (тангенциальная) скорость, R — радиус вращения (орбиты), ω — угловая скорость вращения в радианах в секунду, f — скорость вращения в оборотах в секунду (она же частота вращения в Гц). Когда тело принудительно вращается вокруг некоего центра на подвесе (опоре), то подвес постоянно придаёт ему центростремительное ускорение, заставляя тело отклоняться от прямолинейного движения в сторону центра вращения. В свою очередь, вращающееся тело действует на этот подвес (опору) с центробежной силой, численно равной произведению его массы на центростремительное ускорение. Внимание! В инерциальных системах отсчёта сама центробежная сила в расчётах не учитывается, а учитывается инерция вращающейся массы и сила реакции подвеса или опоры, численно равная центробежной силе, но направленная противоположно — к центру вращения!
Сила Кориолиса
Сила Кориолиса является одной из инерционных сил и проявляется в неинерциальных вращающихся системах отсчёта как дополнительная сила, действующая в плоскости этого вращения на объекты, движущиеся относительно такой вращающейся системы отсчёта пропорционально компонете скорости, перпендикулярной плоскости вращения. Эта сила определяется по формуле FК = 2 · m · [v × ω], где m — масса тела; v — его линейная скорость во вращающейся системе отсчёта; ω — угловая скорость этой системы отсчёта; × — символ векторного произведения.
Гироскопические эффекты
Любое вращающееся твёрдое тело проявляет следующие гироскопические эффекты.
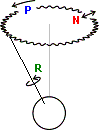
R — собственное вращение,
P — прецессия,
N — нутация.
|
-
При попытке под влиянием внешней силы изменить плоcкость вращения (или, что то же самое, наклон оси), гироскоп стремится сохранить плоскость вращения и наклон своей оси, оказывая сопротивление внешней силе. Однако в первый момент он «подчиняется» этой силе, совершая нутационный бросок. В зависимости от закрепления оси, возможны варианты реакции на наклоняющее воздействие:
-
если оба конца оси свободны — ротор «отскаивает» в сторону без видимого наклона;
-
если один конец оси свободен, а другой закреплён, гироскоп несколько наклоняется;
-
если оба конца оси зафиксированы в плоскости действия прецессионной силы (перпендикулярной направлению действия наклоняющей силы), то наклоняющая сила «транслируется» в опоры оси в виде прецессионной силы, то есть исходная сила как бы «поворачивает» под прямым углом в плоскости вращения ротора.
-
При попытке изменить наклон оси гироскопа, она начинает прецессионное движение. При снятии внешней силы, стремящейся наклонить ось, прецессия немедленно прекращается. Прецессия является проявлением инерционных сил.
-
Во время прецессии гироскоп также испытывает нерегулярные нутационные колебания («подрагивания» оси вращения), заключающиеся в слабом изменении угла нутации — угла между осями собственного и прецессионного вращения тела. В рамках классической физики это явление объяснения не имеет. По некоторым современным представлениям нутация является типичным проявлением так называемых аргументных взаимодействий — основного механизма самоорганизации материи — в данном случае между отклоняющей и прецессионной силами.
Амплитуда нутационных колебаний и скорость прецессии зависят от скорости вращения гироскопа. Изменяя эти параметры воздействием на ось гироскопа, можно изменять скорость его вращения, и наоборот.
 Схема прецессионного эффекта. Более тёмным показаны текущие положение и направление движения, светлым — предполагаемые под действием на ось внешней силы, обозначенной зелёными стрелками. Красным показаны прецессионные силы и момент силы, возникающие из-за инерционных сил при отличии реального движения гироскопа от предполагаемого под действием внешней силы.
Угловая скорость прецессии определяется по формуле Ω = M / (J · ω), где M — момент силы, опрокидывающей гироскоп; J — момент инерции гироскопа; ω — его собственная угловая скорость вращения; формула верна при условии ω >> Ω. В общем случае M = [Ω × L] = dL / dt = d(J · ω) / dt = J · ε, где L — момент импульса гироскопа; ε — его векторное угловое ускорение; × — символ векторного произведения.
Кинетическая энергия вращения. Момент инерции
В общем случае кинетическая энергия тела, вращающегося вокруг какой-либо оси, зависит не только от его массы и скорости вращения, но и от выбора оси вращения и от распределения массы по радиусу относительно этой оси, то есть от формы и состава самого тела. По своей сути задача сводится к суммированию кинетических энергий всех «кусочков» тела, обусловленных их тангенциальной скоростью при вращении вокруг выбранной оси, проходящей внутри тела или вне его.
В случае, если расстояние от оси вращения до центра масс тела много больше геометрических размеров самого тела, тело можно считать «материальной точкой», и его кинетическая энергия вращения достаточно точно определяется как ЕКв = m · v2 / 2 = m · (ω · r)2 / 2 = m · 2 · (π · f · r)2, где m — масса тела, v — его тангенциальная (линейная) скорость, ω — угловая скорость вращения в радианах за секунду, r — расстояние между центром масс и осью вращения, f — частота вращения в оборотах за секунду. Для системы жёстко связанных точечных тел её общая энергия вращения равна сумме энергий каждого из составляющих её тел: EКв = ∑ EКв i. Для тела, размеры которого сравнимы с расстоянием до оси вращения либо если ось вращения проходит внутри него, формой пренебрегать уже нельзя, поэтому необходимо «просуммировать энергию всех его кусочков», т.е. взять интеграл по всему объёму этого тела E = ∫ (ρ · (r · ω)2 / 2) dV, где ρ — это плотность тела в его различных частях; для твёрдого однородного тела плотность и угловая скорость постоянны и их можно вынести из-под интеграла: E = (ω2 · ρ / 2) · ∫ r2 dV.
Момент инерции показывает способность сохранять вращение или противиться раскручиванию для тел различной формы при выборе той или иной оси вращения. Это позволяет получить формулу кинетической энергии вращения, подобную формуле для кинетической энергии линейного движения, где вместо линейной скорости v фигурирует угловая скорость ω, а вместо массы — момент инерции J: EКв = J · ω2 / 2. Если вместо угловой скорости (рад/с) использовать частоту вращения (обороты в секунду, Гц), то EКв = 2 · J · (π · f)2. Момент инерции вычисляется как интеграл по массе или объёму тела с учётом расстояния до оси вращения J = ∫ r2 dm = ∫ ρ · r2 dV. В случае однородного тела постоянную плотность можно вынести из-под интеграла: J = ρ · ∫ r2 dV.
Теорема Штейнера позволяет определить момент инерции тела относительно произвольной оси, если известен его центральный момент инерции — осевой момент инерции для оси, проходящей через центр масс тела и параллельной нужной произвольной оси. Произвольный момент вычисляется по формуле J = Jc + m · s2, где J — искомый момент инерции, Jc — центральный момент инерции, m — полная масса тела, s — расстояние между нужной осью и параллельной ей осью, для которой был определён центральный момент Jc.
В таблице приведены центральные осевые моменты инерции Jс однородных тел массой m для нескольких наиболее распространённых случаев. Если тело представляет собой композицию из этих стандартных форм, его момент инерции можно вычислить как сумму моментов составляющих его элементарных форм с учётом доли общей массы, приходящейся на каждую из них (при наличии отверстий и пустот для них также вычисляются моменты инерции и вычитаются из вычисленного без учёта этих пустот момента инерции той детали, в которой они находятся).
| Форма тела |
Ось вращения |
Момент инерции Jс |
| Плоское кольцо или полый цилиндр любой высоты с тонкими стенками радиусом R |
Вокруг своей оси |
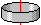 |
m · R2 |
| Плоское кольцо или цилиндр любой высоты с внешним радиусом R и внутренним r |
Вокруг своей оси |
 |
m · (R2 + r2) / 2 |
| Сплошной диск или цилиндр любой высоты радиусом R |
Вокруг своей оси, перпендикулярной плоскости диска |
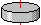 |
m · R2 / 2 |
| Тонкий сплошной диск радиусом R |
Вокруг оси, проходящей через центр диска и лежащей в его плоскости |
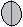 |
m · R2 / 4 |
| Полая сфера с тонкими стенками радиусом R |
Вокруг оси, проходящей через центр |
 |
m · R2 · 2 / 3 |
| Сплошной шар радиусом R |
Вокруг оси, проходящей через центр |
 |
m · R2 · 2 / 5 |
| Тонкий стержень или пластина длиной L |
Вокруг перпендикулярной оси, проходящей через центр |
 |
m · L2 / 12 |
| Тонкий стержень или пластина длиной L |
Вокруг перпендикулярной оси, проходящей через один из концов
|
 |
m · L2 / 3
|
Если тело участвует в нескольких вращательных движениях одновременно (например, планета вращается вокруг собственной оси, вокруг своей звезды и вокруг центра галактики вместе со своей звездой), то общая кинетическая энергия вращения равна сумме энергий всех элементарных вращений. Однако не всегда надо учитывать все вращательные движения. Обычно учитывают лишь те из них, что проявляются в выбранной системе остчёта, либо лишь те, что в рассматриваемой ситуации изменяют свои параметры (скорость и/или ось вращения). Для расчёта воздействия на быстровращающиеся массивные тела необходимо учитывать проявление гироскопических эффектов (прецессию и пр.).
Основные законы аэро- и гидростатики
Закон Паскаля: внешнее давление, воздействующее на жидкость или газ, передаётся этими средами во все стороны равномерно. Поэтому сила давления жидкости или газа всегда направлена по нормали (т.е. перпендикулярно) к каждому элементарному участку поверхности тела, погружённого в них или ограничивающего их.
Закон Архимеда (следствие закона Паскаля): в гравитационном поле на тело, погружённое в жидкость или газ, действует выталкивающая сила, которая противоположна силе тяжести и для однородного тела численно равна FA= (ρср – ρт) · Vт· g, где ρср — удельная плотность среды (жидкости или газа), ρт — удельная плотность однородного тела, Vт — объём тела, погружённый в жидкость или газ, g — ускорение свободного падения в этой точке гравитационного поля.
Давление на глубине P, обусловленное силой тяготения, зависит не от абсолютного веса жидкости или газа, находящихся выше, а лишь от их удельной плотности ρ, высоты столба h (т.е. глубины) и ускорения свободного падения g: P = g · h · ρ. Если плотность сильно меняется с глубиной (актуально прежде всего для газов), придётся брать интеграл P = g · 0H∫ρ(h) dh, где ρ(h) — функция, описывающая зависимость изменения плотности от глубины.
Барометрическая формула описывает зависимость давления газа (атмосферы) от высоты над поверхностью под воздействием силы тяготения в предположении, что температура атмосферы не зависит от высоты: P = P0 · e–μ · g · h / (R · T), где P0 — давление у поверхности, e — основание натуральных логарифмов (2.718281828459...), μ — средний молекулярный вес газа (атмосферы), g — ускорение свободного падения, h — расчётная высота над поверхностью, R — универсальная газовая постоянная, T — абсолютная температура. Для земной атмосферы можно считать h = 8000 · lg(P0 / Ph), где логарифм берётся по основанию 10, или P = P0 / 10h / 8000. Следует заметить, что барометрическая формула лишь весьма приблизительно соответствует реально наблюдаемому изменению давления с высотой, особенно на больших высотах. Температура атмосферы в её нижних слоях падает примерно на 6.5° на каждые 1000 м высоты.
Основные законы аэро- и гидродинамиики
Обычно эти законы даются в дифференциальной форме. Я специально привожу их в интегральном виде — не только для облегчения жизни тех, кто не силён в высшей математике, но и потому, что зачастую трудно определить распределение плотностей, давлений и скоростей во времени и по сечениям потока, а на практике дай Бог достаточно точно измерить хотя бы интегральные значения расхода и скорости или давления на входе и выходе трубы... Именно поэтому формулы сопровождаются оговоркой «для установившейся струи».
Здесь приведены лишь «выжимки» по теме. Для более глубокого изучения гидродинамики рекомендую очень хороший курс лекций, который я нашёл здесь: http://gidravl.narod.ru/index1.html.
Уравнение неразрывности (закон непрерывности потока): для установившейся струи (физически ограниченной трубой переменного сечения и формы либо для «трубки тока», мысленно выделенной из более обширного потока газа или жидкости) всегда выполняется закон постоянства расхода (сколько в трубу втекает, столько же из неё и вытекает) S · v · ρ = const, где S — площадь сечения струи (трубы) в любом месте на её протяжении, v — скорость потока в этом сечении, ρ — удельная плотность вещества потока в этом же месте. Прежде всего это верно для ламинарного потока (без завихрений), однако верно и для общей (интегральной) скорости турбулентного потока. При нагреве или при больших скоростях течения жидкостей возможны кавитационные эффекты — переход части потока из жидкой в газообразную фазу (пар). Однако соотношение продолжает выполняться, если в качестве удельной плотности использовать общую плотность паро-жидкостной смеси в рассматриваемом сечении. Нарушение закона постоянства расхода свидетельствует о нарушении закона сохранения массы — значит, где-то по пути происходит потеря или добавление вещества. Для несжимаемых жидкостей без кавитации (ρ = const) уравнение неразрывности можно упростить до S · v = const.
Уравнение Бернулли: для установившейся струи жидкости или газа в любом её сечении всегда выполняется соотношение ρ · U + P + ρ · v2 / 2 = const, где ρ — удельная плотность потока в этом сечении, U — потенциал объёмных (массовых) сил в этом месте (например, в гравитационном поле он равен h · g — произведению высоты на ускорение свободного падения), P — давление жидкости или газа в рассматриваемом сечении, v — скорость потока в этом сечении. Первый член уравнения Бернулли, записанного в такой форме, является удельной потенциальной энергией, второй — давлением, а третий — скоростным напором. Для струи жидкости уменьшение на каком-либо участке давления P ниже некоторой величины, равной давлению фазового перехода этой жидкости (обычно это достаточно малые величины), указывает на переход части жидкости в пар — кавитационный эффект. В техническом приложении уравнение Бернулли выглядит так: ρ · U + P + ρ · v2 / 2 + Q'T + A' = const, где Q'T — удельные потери давления на гидродинамическое трение (не путать с гидродинамическим сопротивлением!), A' — удельная полезная работа, выполненная потоком (например, вращение турбины).
Максимальная скорость свободного (в атмосферу, а не в жидкость) истечения жидкости под напором (закон Торричелли): v∞ = √(2 · g · h) = √(2 · ΔP / ρ), где √ — квадратный корень; g — ускорение свободного падения; h — напор (высота столба жидкости над уровнем истечения); ΔP — избыточное давление жидкости в резервуаре относительно внешней среды на уровне истечения; ρ — плотность жидкости. Эта формула верна при отсутствии дополнительных ускоряющих воздействий, поскольку в соответствии с законом Бернулли всё давление переходит в скоростной напор. Однако даже при дополнительном ускорении, скажем, под воздействием гравитации, ламинарный поток внутри узкой трубы, ограниченный её стенками, обычно не может набрать большую скорость, поскольку при дроблении струи в случае превышения этой скорости возник бы вакуум, и поэтому атмосферное давление у внешнего конца трубы будет тормозить «слишком быстрые» порции воды, создавая тормозящее обратное давление в потоке и обеспечивая неразрывность струи внутри трубы. Впрочем, очень большое усилие (скажем, в центробежных конструкциях) может всё же «порвать» поток, вызвав явление кавитации. Свободная струя при превышении этой скорости под действием силы тяжести начинает дробиться на капли (происходит нарушение неразрывности струи), поскольку разрывы тут же заполняются окружающим воздухом и вакуума, а следовательно, и тормозящего давления, не возникает. То же явление будет происходить и по мере увеличения диаметра трубы, когда благодаря возникающей турбулентности потока воздух сможет проникать в трубу против опускающейся жидкости.
Скорость течения вязкой жидкости в длинной трубке: v = (ΔP / η) · R2 / (8 · l), где ΔP — разность давлений на концах трубки, η — вязкость жидкости или газа (сильно зависит от температуры), R — внутренний радиус трубки, l — её длина, l >> R.
Число Рейнольдса Re = v · d / ν = v · d · ρ / η (безразмерная величина) определяет режим течения в трубе, где v — средняя скорость течения в трубе, определяемая исходя из расхода в единицу времени и сечения трубы; d — внутренний диаметр трубы; ν — кинематическая вязкость; ρ — удельная плотность; η — динамическая вязкость. В случае круглых труб для чисел Рейнольдса меньше критического значения 2300 течение считается безусловно ламинарным, выше 4000 — безусловно турбулентным.
Напор переводится в мощность и давление следующим образом: WT = qV · PТ = qV · HТ · g · ρ = q · HТ · g, где WT — мощность, затрачиваемая на трение, qV — объёмный расход жидкости, м3/с, PТ — потери давления на трение, HТ — потери напора на трение, g — ускорение свободного падения, ρ — удельная плотность жидкости, q — массовый расход жидкости, кг/с.
Потери напора на гидравлическое трение HТ (высота условного столба жидкости) в круглой трубе (универсальная формула Вейсбаха-Дарси): HТ = λ · (l / d) · v2 / (2 · g), где λ — безразмерный коэффициент гидравлического трения, l — длина трубы, d — её внутренний диаметр, v — усреднённая скорость потока (вычисляемая по расходу), g — ускорение свободного падения.
Безразмерный коэффициент гидравлического трения λ:
• при ламинарном потоке λ = 64 / Re (при числе Рейнольдса Re < 2300 Т.М.Башта рекомендует использовать λ = 75 / Re);
• при турбулентном потоке λ дополнительно зависит от эквивалентной шероховатости ΔЭ:
• • для гидравлически гладких труб, 4000 < Re < 10 · (d / ΔЭ): λ = 0.3164 / Re0.25 (полуэмпирическая формула Блазиуса для Re = 4000..100000) или λ = 1 / (1.8 · lg(Re) – 1.5)2 (эмпирическая формула П.К.Конакова) либо λ = 1.01 / lg(Re)2.5 (формула ВТИ для Re = 4000..6300000);
• • для промежуточного случая: λ = 0.11 · (ΔЭ / d + 68 / Re)0.25 (универсальная формула А.Д.Альтшуля);
• • для сильно шероховатых труб, Re > 560 · (d / ΔЭ): λ = 0.11 · (ΔЭ / d)0.25 (упрощённая формула А.Д.Альтшуля) или λ = 1 / (2 · lg(ΔЭ / (3.71 · d)))2 (формула Прандтля-Никурадзе).
Номограммы на основе расчётных и экспериментальных данных приведены здесь.
Потери напора при изменении сечения трубы: hИ = ζ · v2 / (2 · g), где ζ — коэффициент потерь; v — скорость в меньшей из сопрягающихся труб (более высокая скорость); g — ускорение свободного падения. Коэффициент потерь ζ зависит от вида изменяющегося сечения:
• при внезапном расширении (маленькая круглая труба резко превращается в соосную ей большую) ζ = (1 – S1 / S2)2, где S1 и S2 — площади сечения маленькой (входной) и большой (выходной) труб соответственно (следствие теоремы Борда);
• при внезапном сужении (большая круглая труба резко превращается в соосную ей маленькую) ζ = (1 – S2 / S1) / 2, где S1 и S2 — площади сечения большой (входной) и маленькой (выходной) труб соответственно (полуэмпирическая формула И.Е.Идельчика).
Дополнительные сведения об истечении струй можно найти на странице, посвящённой эффекту Котоусова.
Зависимость между объёмом и давлением газа: при хорошем теплообмене с окружающей средой для сжимаемого газа P · V = const, где P — давление газа, а V — его объём, т.е. насколько возрастёт давление, настолько же уменьшится объём, и наоборот. По сути, является частным случаем уравнения Менделеева-Клапейрона для изотермических процессов.
Термодинамика
Классическая термодинамика, до сих пор преподаваемая в школах и ВУЗах в качестве единственной общедоступной версии процессов, связанных с тепловыми эффектами, основана на молекулярно-кинетической теории (МКТ). К сожалению, МКТ морально давно устарела, а лежащие в её основе положения часто имеют мало общего с происходящими в реальности процессами. Тем не менее, основные используемые на практике термодинамические закономерности, такие как уравнение состояния идеального газа, были получены эмпирическим путём и достаточно адекватно отражают процессы, происходящие в наиболее часто встречающихся ситуациях. Поэтому феноменологическая термодинамика остаётся полезной и актуальной, в отличии от «объясняющей» и «обосновывающей» её МКТ, — конечно, при условии понимания эмпирического характера используемых закономерностей и связанных с этим ограничений области их корректного применения. Однако в разделе приведены и некоторые базовые понятия МКТ, поскольку они до сих пор слишком широко используются в обучении, инженерной и научной деятельности.
Термодинамические величины
В дополнение к механическим величинам, из которых наиболее широко используются понятия объёма, давления, работы и энергии, в термодинамике вводится базовое понятие температуры и несколько вспомогательных понятий.
| Понятие |
Обозначение и формула |
Единица измерения |
|
Температура (характеризует отдаваемый объектом удельный поток энергии, обусловленный тепловым возбуждением вещества; по МКТ — мера кинетической энергии теплового движения частиц тела). Определяет возможную интенсивность и направление обмена тепловой энергией с другими объектами.
|
T |
кельвин (К) |
|
Количество тепла, теплота (мера внутренней тепловой энергии тел как макрообъектов)
|
Q |
джоуль (Дж)
|
Удельная теплоёмкость (мера изменения температуры тела при изменении запасённого им количества тепла) зависит от текущего термодинамического состояния тела.
Различают теплоёмкость при изобарическом процессе (cP) и теплоёмкость при изохорическом процессе (cV) — для твёрдых и жидких тел они очень близки, для газов существенно различаются
|
c =ΔQ / (ΔT · m) |
Дж / (кг · К)
|
|
Удельная теплопроводность (мера скорости передачи теплоты внутри тела) зависит от текущего термодинамического состояния тела
|
λ = (ΔQ · t) / (ΔT · l) |
Вт / (м · К)
|
Основные понятия классической термодинамики
Агрегатное состояние вещества — форма существования вещества, отличающаяся от других его агрегатных состояний механической реакцией на внешние механические же воздействия (давление, наличие ограничивающих стенок, гравитацию и пр.). Выделяют три основных агрегатных состояния — твёрдое, жидкое и газообразное. Твёрдое вещество стемится сохранить как свой объём, так и форму, жидкое — только объём, а у газообразного вещества внешние обстоятельства полностью определяют как форму, так и объём. В качестве четвёртого агрегатного состояния иногда называют плазму, считая её поведение в некоторых ситуациях принципиально отличным от поведения «обычных» газов. Однако существует мнение, что плазма является особым фазовым состоянием газообразного вещества. Изменение агрегатного состояния также называют «фазовым переходом первого рода».
Адиабатический процесс — термодинамический процесс, при рассмотрении которого обмен тепловой энергией с окружающей средой можно не учитывать. Прежде всего к таким процессам относятся очень быстрые процессы, а также более медленные процессы, происходящие в условиях хорошей теплоизоляции.
Изобарический процесс — термодинамический процесс, при рассмотрении которого давление считается постоянным. Чаще всего к этой категории можно отнести не слишком быстрые процессы, происходящие «на открытом воздухе».
Изотермический процесс — термодинамический процесс, при рассмотрении которого температура считается постоянной. Обычно к этой категории относятся медленные процессы, происходящие «на открытом воздухе» либо в условиях хорошего теплообмена с окружающей средой. К этой же категории иногда можно отнести и те адиабатические процессы, при которых давление и объём меняются несильно — на проценты, а не в разы, — поскольку в этом случае изменения температуры невелики и тогда (но не всегда!) ими можно пренебречь.
Изохорический процесс — термодинамический процесс, при рассмотрении которого объём считается постоянным. Как правило, к этой категории относятся процессы, происходящие внутри закрытых прочных резервуаров.
Идеальный газ — газ, в котором все взаимодействия его частиц между собой являются идеальными упругими столкновениями. Кроме того, часто подразумевается, что он не обладает вязкостью, а все изменения давления и температуры распространяются сразу на весь его объём. Этим критериям достаточно хорошо отвечает воздух при нормальных комнатных условиях и разреженные газы, занимающие не слишком большой объём. Разделение газов на «реальный» и «идеальный» является следствием использования МКТ. На самом деле главным аспектом идеальности газа является предположение о том, что вся механическая энергия его частиц всегда находится только в кинетической форме, в то время как в реальных газах она постоянно перераспределяется между кинетической и потенциальной формами, причём доля последней растёт с ростом концентрации частиц газа, т.е. с ростом давления.
Идеальная жидкость — жидкость, которая не обладает поверхностным натяжением и вязкостью (сверхтекучая жидкость). Кроме того, часто подразумевается, что все изменения давления и температуры распространяются сразу на весь её объём. По сути, идеальная жидкость является несжимаемым идеальным газом.
Реальный газ — все газы, не соответствующие определению идеального газа. Традиционно в качестве реального газа рассматривают газы, обладающие заметной вязкостью, прежде всего газы под большим давлением, многоатомные газы, а также иногда имеются в виду газы, занимающие большой объём, где нельзя не учитывать конечную скорость распространения изменения состояния. Разделение газов на «реальный» и «идеальный» является следствием использования МКТ.
Фазовое состояние вещества — форма существования вещества, при которой в случае плавного изменения внешних параметров (температуры, давления и др.) его состояние остаётся практически неизменными. При изменении температуры, давления или других условий более определённых пределов, фазовое состояние может измениться, что сопровождается резким изменением существенных параметров (прочности, твёрдости, теплоёмкости, удельной плотности, электрических, магнитных, оптических и других свойств), а также выделением или поглощением энергии. Смены агрегатного состояния вещества (также называемые «фазовыми переходами первого рода») всегда являются сменой фазового состояния, однако в рамках одного агрегатного состояния при разных комбинациях внешних условий некоторые вещества могут существовать в нескольких различных фазовых состояниях, скажем твердые тела — с разными типами кристаллических решёток (примеры: уголь / графит / алмаз или мартенситное и аустенитное состояния металлов и сплавов). Изменение фазового состояния в рамках одного и того же агрегатного состояния называют «фазовым переходом второго рода».
Основные законы классической термодинамики
В термодинамических формулах фигурируют абсолютные значения давления и температуры, то есть давление меряется относительно вакуума, а температура измеряется в кельвинах.
Первый закон термодинамики: ΔU = ΔQ + ΔA, где ΔU изменение внутренней энергии тела, ΔQ — количество теплоты, переданной телу или отнятой у него, ΔA — работа, совершённая телом во время этого процесса.
Второй закон термодинамики: тепло не может самопроизвольно перейти от более холодного тела к более горячему без каких-либо других изменений в системе. Общепризнанным примером невыполнения этого закона являются эпизоды подъёма тяжёлых броуновских частиц вверх в ходе их хаотического движения. Считается, что в этом случае увеличение потенциальной энергии броуновских частиц осуществляется за счёт кинетической энергии окружающих их частиц среды и сопровождается некоторым охлаждением ближайшего к ним микрообъёма. Поэтому данный закон постулируется эмпирически, и считается, что на макроуровне он выполняется достаточно строго, поскольку опровергающие это общепризнанные факты отсутствуют.
Третий закон термодинамики: теплоёмкость любого тела при приближении его температуры к абсолютному нулю также стремится к нулю.
Закон состояния идеального газа (уравнение Менделеева-Клапейрона) связывает объём, температуру и давление идеального газа: P · V = (m / μ) · R · T, где P — давление газа; V — его объём; T — температура; R — универсальная газовая постоянная (для СИ следует брать значение с кг-моль); m — масса этого газа; μ — для СИ килограмм-моль, т.е. число килограммов вещества, численно равное его молекулярному весу (в 1 килограмм-моле вещества всегда находится одинаковое число молекул, равное числу Авогадро).
Уравнение адиабаты для идеального газа: P · Vγ = const, где P — давление газа, V — его объём, γ = cP / cV — соотношение его изобарической и изохорической теплоёмкостей (всегда больше 1). Отсюда следует изменение температуры при адиабатических процессах: T1 / T2 = (P1 / P2) · (V1 / V2)γ, причём γ зависит от температуры, и в случае сильного изменения объёма и давления (раз в 10 и более) это может быть существенным. Применимо для относительно медленных процессов, когда температуры газа и ограничивающего газ слоя стенок успевают уравниваться, но теплообмен с внешней средой очень мал.
Уравнение Клапейрона — Клаузиуса определяет условие равновесия фаз (твёрдое тело ↔ жидкость ↔ газ): dP / dT = q / (T · (V1 – V2), где P — давление, T — температура, V — объём, q — удельная теплота фазового перехода.
Работа при изотермическом расширении или сжатии: A = P1 · V1 · ln(P2 / P1), где индекс «1» обозначает исходное состояние системы, а «2» — конечное.
Электромагнетизм
Электрические и магнитные величины
| Понятие |
Обозначение и формула |
Единица измерения |
|
Электрический заряд (мера количества электричества)
|
q |
кулон (Кл)
|
|
Сила тока (мера скорости изменения электрического заряда)
|
I = q / t |
ампер (А = Кл / с)
|
|
Разность электрических потенциалов, электрическое напряжение (мера работы, которую может совершить заряд под воздействием электрического поля)
|
U = A / q |
вольт (В = Дж / Кл)
|
|
Электрическая ёмкость (мера способности системы тел удерживать заряд) зависит от многих факторов, прежде всего от материала элементов, параметров разделяющей их среды и геометрии системы
|
C = q / U |
фарад (Ф = Кл / В)
|
|
Напряжённость электрического поля (мера пространственного градиента электрического потенциала в той или иной точке, то есть изменения этого потенциала при малом перемещении в определённом направлении)
|
E = U / s |
В / м
|
Индукция электрического поля (мера проявления электростатической силы в конкретной среде).
Не путать с индуктивностью!
|
D = εa · E |
Кл / м2
|
Диэлектрическая проницаемость среды (отношение электрической индукции к электрической напряжённости, т.е. мера способности среды к проявлению в ней электростатической силы) у разных материалов может сильно зависеть от различных внешних факторов, в частности от температуры.
Различают абсолютную диэлектрическую проницаемость εa и относительную диэлектрическую проницаемость ε = εa / ε0 (отношение абсолютной диэлектрической проницаемости среды к диэлектрической проницаемости вакуума).
В системе СИ диэлектрическая проницаемость вакуума ε0 = 8.85·10–12 Ф/м (диэлектрическая постоянная СИ).
Относительная диэлектрическая проницаемость ε является безразмерной величиной.
|
εa = D / E
|
Ф / м
|
Электрическое сопротивление (мера соотношения напряжения и тока на участке электрической цепи). Обратная величина — проводимость — на практике используется крайне редко.
Различают активное и реактивное сопротивление. Активное сопротивление проявляется как при постоянном, так и при переменном токе, при этом электрическая энергия преобразуется в другие формы (тепло, внешняя механическая работа, свет и т.д.) и теряется безвозвратно. Реактивное сопротивление проявляется лишь при изменяющемся токе (переменном или в моменты включения и выключения постоянного тока). Элементы, обладающие реактивным сопротивлением, запасают энергию и препятствуют изменению воздействующего на них напряжения (ёмкости) или тока (индуктивности).
|
R = U / I |
ом (Ом = В / А)
|
|
Удельное электрическое сопротивление (мера способности вещества препятствовать прохождению электрического тока)
|
ρ = R · S / l
|
Ом · м
|
|
Напряжённость магнитного поля (мера магнитного поля в вакууме, при отсутствии физической среды).
|
H |
А / м |
Магнитная индукция (мера проявления магнитного поля в конкретной среде).
Не путать с индуктивностью!
|
B = μa · H
|
тесла (Тл)
|
Магнитная проницаемость среды (отношение магнитной индукции к напряжённости магнитного поля, т.е. мера способности среды к проявлению в ней магнитных сил) у разных материалов может сильно зависеть от различных внешних факторов, в частности от температуры.
Различают абсолютную магнитную проницаемость μa и относительную магнитную проницаемость μ = μa / μ0 (отношение абсолютной магнитной проницаемости среды к магнитной проницаемости вакуума).
В системе СИ магнитная проницаемость вакуума μ0 = 4π·10–7 ~ 1.26·10–6 Гн/м (магнитная постоянная СИ).
Относительная магнитная проницаемость μ является безразмерной величиной.
|
μa = B / H
|
Гн / м
|
|
Магнитный поток (мера взаимодействия магнитного поля с электрическим контуром)
|
Φ = S · |B · n|
|
вебер (Вб = Гн · А)
|
Индуктивность (мера способности участка цепи с помощью магнитного поля препятствовать изменению протекающего через него тока); как и ёмкость, зависит от многих факторов, прежде всего от материала элементов, параметров разделяющей их среды и геометрии системы.
Не путать с электрической или магнитной индукциями!
|
L |
генри (Гн = Ом · с)
|
Общее описание электромагнитного взаимодействия
В современной физике считается, что все электромагнитные взаимодействия неподвижных и движущихся зарядов между собой и с электромагнитным полем описываются с помощью силы Лоренца и уравнений Максвелла.
На заряд, движущийся в электромагнитном поле, действует сила Лоренца, вычисляемая по формуле F = q · (E + [v × B]), где надчёркивание означает векторный характер величины; q — величина заряда; E — векторная напряжённость электрического поля; v — векторная скорость заряда; B — векторная индукция магнитного поля; символ «×» означает векторное произведение величин, заключённых в квадратные скобки. Ниже приведены частные случаи для электрического и магнитного полей.
Для большинства людей уравнения Максвелла в общем виде весьма сложны для понимания, а тем более для их практического применения. Тем не менее, на практике очень часто вполне достаточно воспользоваться их точными решениями для частных случаев. В частности, в соответствии с уравнениями Максвелла движущийся заряд создаёт электрическое поле напряжённостью
E = (q / (4π · ε · ε0)) · (r / r3) · (1 – v2 / c2) / (1 – [n × v]2 / c2)3/2 = (n · q / (4π · ε · ε0 · r2)) · (1 – v2 / c2) / (1 – [n × v]2 / c2)3/2
и магнитную индукцию
B = (ε · μ / c2) · [v × E],
где в дополнение к обозначениям для силы Лоренца r — вектор от заряда к точке измерения напряжённости поля, r — модуль, т.е. длина этого вектора (расстояние между точкой измерения и зарядом); n — единичный вектор, направленный от заряда к точке измерения напряжённости поля (равен отношению r / r); ε и ε0 — относительная диэлектрическая проницаемость и диэлектрическая проницаемость вакуума; μ — магнитная проницаемость; c — скорость распространения электромагнитных возмущений в вакууме (скорость света). [n × v]2 равно квадрату длины проекции вектора v на плоскость, перпендикулярную единичному вектору n. Электростатика
Частным следствием из вышеприведённых формул является закон Кулона, описывающий силу взаимодействия точечных взаимно неподвижных зарядов (электростатическую силу): F = –q1 · q2 / (4π · ε0 · ε · r2), где q1 и q2 — величины взаимодействующих зарядов с учётом их знака; ε0 — диэлектрическая проницаемость вакуума; ε — относительная диэлектрическая проницаемость; r — растояние между зарядами; отрицательная сила соответствует отталкиванию, а положительная — притяжению зарядов друг к другу.
Ёмкость плоского конденсатора определяется площадью меньшей обкладки S и расстоянием между обкладками d: C = ε0 · ε · S / d. Ёмкость цилиндрического конденсатора и коаксиального кабеля: C = 2π · ε0 · ε · l / ln(b / a), где l — высота конденсатора (длина кабеля); b — радиус внешнего цилиндра (обкладки); a — радиус внутреннего цилиндра (обкладки). Ёмкость сферического конденсатора: C = 4π · ε0 · ε / (1 / a – 1 / b), где b — радиус внешней сферы; a — радиус внутренней сферы. Ёмкость двухпроводной линии: C = π · ε0 · ε · l / ln(d / r), где l — длина линии; d — расстояние между осями параллельных проводов; r — их радиус.
Энергия, запасённая в заряженном конденсаторе: E = C · U2 / 2, где C — ёмкость этого конденсатора, U — напряжение на его обкладках. Формула «симметрична» энергии катушки индуктивности.
Постоянный электрический ток
Электрический ток — это упорядоченное движение зарядов. Это движение порождается электродвижущей силой (ЭДС) источника тока, которая численно равна работе сторонних сил по перемещению единицы положительного заряда с одного контакта (полюса) источника на другой. Сторонними называются силы, по своей природе отличающиеся от электрических (механические, химические и др.), которые внутри источника тока переносят заряды против действия электрических сил (положительные заряды — от отрицательного полюса к положительному). Вся работа в электрической цепи совершается за счёт ЭДС источника, т.е. в конечном счёте за счёт этих сторонних сил. ЭДС измеряется в тех же единицах, что и напряжение, т.е. в вольтах.
Направление тока определяется движением положительных зарядов (от «плюса» к «минусу»), поэтому отрицательные электроны, в большинстве случаев являющиеся реально движущимися носителями зарядов, движутся в сторону, обратную номинальному направлению тока.
Электрическая цепь — совокупность источников тока, соединительных проводов, электрических приборов и других устройств, в которых ток производит работу.
Закон Ома для неразветвлённого участка цепи (двухполюсника), на котором не действуют сторонние силы: I = U / R, где I — сила тока в данном участке цепи; U — напряжение на концах этого участка; R — электрическое сопротивление этого участка.
Работа электрического тока на участке цепи определяется силой тока I и напряжением U на этом участке, а также временем их действия t: A = U · I · t.
Мощность электрического тока W = U · I.
Первое правило Кирхгофа: алгебраическая (с учётом знака) сумма силы токов, сходящихся в любой точке разветвления цепи, равна нулю — сколько тока втекает в узел цепи, столько и вытекает оттуда.
Второе правило Кирхгофа: для любого замкнутого контура, выделенного из разветвлённой цепи, алгебраическая сумма произведений сил токов на соответствующие сопротивления равна алгебраической сумме всех электродвижущих сил в этом контуре — суммы напряжений и ЭДС в контуре равны.
Электромагнетизм
Сила Ампера, действующая на малый участок проводника с током: ΔF = I · Δl · B · sin(β), где I — сила тока в проводнике; Δl — длина этого малого (элементарного) участка проводника; B — индукция магнитного поля; β — угол между направлениями магнитной индукции и протекания тока по проводнику.
Сила взаимодействия двух параллельных проводников с током: F = μ · μ0 · I1 · I2 · l / (2π · r), где μ — относительная магнитная проницаемость среды; μ0 — абсолютная магнитная проницаемость вакуума; I1 и I2 — сила тока в соответствующих проводниках; l — длина проводников; r — расстояние между проводниками (намного меньшее их длины).
Магнитная индукция в точке пространства. Для движущегося заряда B = ((μ0· μ) / (4 · π)) · (q / r3) · [r v], где μ0 — магнитная постоянная СИ; μ — относительная магнитная проницаемость, раз; q — величина движущегося движущегося заряда; r — расстояние до этого заряда; [r v] — проекция нормали вектора скорости заряда v на плоскость, перпендикулярную направлению на него. Для бесконечного прямого проводника с током B = ((μ0· μ) / (4π)) · (2 · I / r), где в дополнение к предыдущим обозначениям I — сила тока, текущего по проводнику; r — расстояние до проводника. Это частные случаи, общим решением являются уравнения Максвелла.
Сила Лоренца в скалярном представлении при отсутствии электрического поля: F = q · v · B · sin(α), где q — величина заряда, движущегося в магнитном поле; v — скорость заряда; B — индукция магнитного поля; α — угол между скоростью заряда и направлением магнитной индукции.
Момент силы при воздействии магнитного поля на плоский контур: M = I · S · B · sin(α), где I — сила тока в контуре; S — площадь контура; B — индукция магнитного поля; α — угол между нормалью к плоскости контура и направлением магнитной индукции. Величина pm = I · S называется магнитным моментом.
Энергия катушки индуктивности: E = L · I2 / 2, где L — индуктивность катушки, I — сила тока через обмотку катушки. Формула «симметрична» энергии конденсатора.
Индуктивность соленоида с сердечником: L = μ0· μ · n2 · (S / l) · k, где μ0 — магнитная постоянная СИ; μ — относительная магнитная проницаемость сердечника (для ферромагнетиков зависит и от его формы); n — число витков; S — площадь внутреннего сечения соленоида (сечение сердечника); l — длина намотки; k — коэффициент, определяемый соотношением длины намотки l и её диаметра d.
| Отношение длины и диаметра намотки l/d |
0.1 |
0.5 |
1 |
5 |
≥10 |
| k |
0.2 |
0.5 |
0.6 |
0.9 |
1.0 |
Фотоны и электромагнитное излучение
На данный момент меня интересуют не столько оптические, сколько энергетические характеристики электромагнитных излучений. Поэтому, хотя к таким излучениям относится и видимый свет, в названии этого раздела нет слова «оптика».
Сила давления света на поверхность: F = (1 + θ) · W / c, где F — сила, вызванная давлением света; θ — коэффициент отражения с учётом угла между потоком света и плоскостью поверхности (для абсолютно чёрного тела ρ=0, для идеального зеркала, перпендикулярного потоку света, ρ=1); W — мощность потока излучения, приходящегося на эту поверхность, Вт; c — скорость света.
Связь между частотой и длиной волны излучения: f = c / λ, где f — частота излучения; c — скорость света в среде; λ — длина волны в этой же среде.
Зависимость энергии фотона от частоты излучения и длины волны: Eф = h · f = h · c / λ, где h — постоянная Планка; f — частота излучения; c — скорость света в среде; λ — длина волны в этой же среде.
Механический импульс фотона: p = E / c, где E — энергия фотона; c — скорость света в среде.
Внешний фотоэффект: h · f = Aφ + me · vмакс2 / 2, где h — постоянная Планка; f — частота излучения; Aφ — работа выхода электрона для данного вещества; me — масса электрона; vмакс — максимально возможная скорость электрона, выбитого из вещества квантом излучения.
Излучательная способность тела (закон Кирхгофа): EλT / ΛλT = ελT, где EλT — излучательная способность тела в зависимости от длины волны излучения и температуры; ΛλT — поглощательная способность тела в зависимости от длины волны излучения и температуры (для абсолютно чёрного тела всегда 1); ελT — постоянна для всех тел при данных длине волны излучения и температуре. Суть закона Кирхгофа заключается в том, что соотношение излучательной и поглощательной способности тела не зависит от его природы, а определяется только температурой и длиной волны излучения.
Полная мощность излучения абсолютно чёрного тела в полном диапазоне длин волн в зависимости от температуры (закон Стефана-Больцмана): Wизл = σ · T4, где σ — постоянная Стефана-Больцмана; T — абсолютная температура.
Зависимость длины волны максимальной излучательной способности абсолютно чёрного тела от температуры (закон смещения Вина): λмакс = c1 / T, где λмакс — длина волны, соответствующая максимальной излучающей способности; c1 — постоянная Вина; T — абсолютная температура.
Испускательная способность абсолютно чёрного тела (формула Планка): ελT = (2π · c2 / λ5) · h / (eh · c / (k · λ · T) – 1), где ελT — испускательная способность в зависимости от длины волны излучения и температуры; c — скорость света в вакууме; λ — длина волны; k — постоянная Больцмана; h — постоянная Планка; T — абсолютная температура.
Оценка эффективности (КПД) источника света для излучения с длиной волны 555 нм (зелёный свет): η = Φ / (683 · W), где Φ — световой поток от источника, лм; W — потребляемая источником мощность, Вт.
Элементы квантовой механики
Длина волны де Бройля для частицы: λ = h / p = h / (m · v), где h — постоянная Планка, p — импульс частицы, m — её масса, v — скорость в выбранной системе отсчёта. Частота де Бройля для той же частицы: f = E / h = m · c2 / h, где E — энергетический эквивалент массы частицы, с — скорость света в вакууме. Таким образом, дебройлевская частота не зависит от системы отсчёта, а длина волны — зависит, и в системе отсчёта, где частица неподвижна, её длина волны де Бройля становится бесконечно большой. Статистическй смысл: квадрат амплитуды волны де Бройля в данной точке является мерой вероятности того, что данная частица обнаружится в этой точке. Подтверждается дифракционными картинами, полученными при рассеивании пучков частиц на кристаллах.
Комптоновская длина волны для частицы: λC = h / (m · c), где h — постоянная Планка, m — масса частицы, с — скорость света в вакууме. Можно сказать, что это длина волны де Бройля для частицы, движущейся со скоростью света (минимально возможная дебройлевская длина волны). Физический смысл: мелкие частицы нельзя рассматривать как точечные объекты в пределах области, размеры которой не превышают их комптоновской длины волны, — они как бы «размазаны» внутри этой области. Для частиц, имеющих большую интенсивность перехода в промежуточные состояния (например, нуклонов), в качестве размера «зоны неопределённости» следует брать λC для наиболее лёгкой из частиц, образующихся при таких трансформациях (т.е. наибольшую).
Физические константы и стандартные величины
Универсальные физические константы
В современной физике эти величины считаются неизменными во всей известной человечеству части Вселенной. В скобках указаны значащие цифры, попадающие в пределы погрешности измерений при определении той или иной константы.
| Название |
Обозначение |
Значение |
| Гравитационная постоянная |
G |
(6.67428±0.00067)·10–11 м3 / (кг · с3) |
| Универсальная газовая постоянная (постоянная Менделеева) |
R |
8.31441±0.00026 Дж · моль / К
8314.41±0.26 Дж · кг-моль / К
|
| Число Авогадро |
NA |
6.02214179(30)·1023 моль–1
6.02214179(30)·1026 кг-моль–1
|
| Постоянная Больцмана |
k = R / NA |
1.3806504(24)·10–23 Дж / К |
| Масса протона |
mp |
1.672621637(83)·10–27 кг |
| Масса электрона |
me |
9.10938215(45)·10–31 кг |
| Заряд электрона |
e |
–1.602176487(40)·10–19 Кл |
| Скорость света в вакууме |
c |
2.99793·108 м / с |
| Постоянная Планка |
h |
6.62606896(33)·10–34 Дж · с |
| Постоянная Дирака (она же приведённая постоянная Планка) |
ћ = h / (2π) |
1.054571628(7)·10–34 Дж · с |
| Постоянная Стефана-Больцмана |
σ |
5.670400·10–8 Вт / (м2 · K4) |
| Постоянная Вина |
c1 |
2.8999·10–3 м · K |
Стандартные физические величины
Эти величины часто воспринимаются как физические константы, однако на самом деле они верны лишь для стандартных условий на поверхности Земли или связаны с использованием конкретной системы единиц измерения.
| Название |
Обозначение |
Значение |
Ускорение свободного падения на поверхности Земли
|
g |
9.832 м / c2
9.780 м / c2
9.80665 м / c2
9.81 м / c2
|
Объём моля идеального газа при нормальных условиях
Объём килограмм-моля при тех же условиях
|
Vμ
|
0.0224207 м3 = 22.4207 л
22.4207 м3
|
|
Диэлектрическая проницаемость вакуума в системе СИ (диэлектрическая постоянная СИ)
|
ε0 |
8.85·10–12 Ф / м |
|
Магнитная проницаемость вакуума в системе СИ (магнитная постоянная СИ)
|
μ0 |
4π·10–7 ~ 1.26·10–6 Гн / м |
♦
|