Явление гидравлического удара
Гидравлический удар представляет собой кратковременное, но резкое и сильное повышение давления в трубопроводе при внезапном торможении двигавшегося по нему потока жидкости. Как правило, это явление возникает при заполнении трубопроводов, когда воздух успевает выйти через специально открытый кран, но сечения этого крана не хватает, чтобы пропустить весь поток внезапно достигшей его несжимаемой жидкости. Такой же эффект возникает и при быстром закрытии вентиля, резко перекрывающего поток. Последнее особенно актуально в наши дни, когда старые винтовые кран-буксы, поневоле закрывавшиеся плавно (ведь крутить маховичок надо много оборотов, и потому шток перекрывает просвет вентиля достаточно медленно), заменяются современными шаровыми кранами, «перерезающими» поток всего за четверть оборота одним движением руки.
Однако гидроудары не обязательно распространяются на всю трубу. При возникновении кавитации, каждое схлопывание кавитационного пузырька сопровождается микро-гидроударом. Таким гидроударам не под силу разрушить всю трубу, однако их длительное разрушительное действие в зоне кавитации легко может превысить ущерб от мощных, но относительно редких гидроударов.
Явление гидравлического удара может быть не только разрушительным, но и созидательным — например, именно с его помощью мирно поднимают воду необычные устройства под названием «гидравлический таран».
В любом случае, как для нейтрализации, так и для использования гидроудара, необходимо не только понять его природу, но и рассчитать его параметры. Этим мы и займёмся. В отличие от традиционного гидродинамического подхода, где обычно оперируют напором (по сути, это псевдоним давления), здесь это явление будет рассматриваться с общефизической точки зрения, и давление будет фигурировать без всяких псевдонимов.
Описание явления
Фазы развития гидроудара
Факторы, влияющие на силу гидроудара
Особенности явления гидроудара
Высокая скорость процесса
Условия отрыва жидкости. Сильные и слабые гидроудары
Повторные циклы
Размер имеет значение
Расчёт параметров гидравлического удара
Расчёт повышения давления при гидроударе. Формула Жуковского
Расчёт длительности стадий сжатия и разрежения у заглушки
Длительность стадии сжатия
Длительность стадии разрежения
Расчёт длительности стадий сжатия и разрежения в произвольном месте трубы
Расчёт ускоряющегося потока
Где ускоряется жидкость?
Гашение ударной волны
Расчёт скорости заполняющего трубу потока для сверхтекучей жидкости
Расчёт скорости заполняющего трубу потока с учётом гидравлического трения
Особые случаи
Гидроудар в частично заполненной трубе
Гидроудар в частично заполненной горизонтальной трубе
Гидроудар в частично заполненной вертикальной трубе
Гидроудар в результате столкновения потоков
Гидроудар с утечками (неполный гидроудар)
Гидроудар с боковой утечкой
Гидроудар с торцевой утечкой
Расчёт гидроудара с утечкой
Гидроудар с большими утечками
О сверхъединичности гидроударов
Описание явления
Более-менее заметно гидравлический удар проявляется только в жёстких трубопроводах при большой скорости потока. Он происходит тогда, когда движущаяся с некоторой скоростью жидкость вдруг встречает на своём пути жёсткое препятствие, которым, как правило, бывает заслонка или заглушка. В подобной ситуации пресловутый cтальной шарик в вакууме просто отскочил бы от встретившейся стенки обратно с той же скоростью, с которой подлетел к ней. Однако жидкость — не шарик, да и вокруг не вакуум, а жёсткие стенки, а сзади напирают следующие порции, которые ещё «не знают», что впереди прохода нет! В результате жидкость останавливается, а её кинетическая энергия превращаются в потенциальную — потенциальную энергию упругого сжатия жидкости (ведь жидкости считаются несжимаемыми лишь по сравнению с газами, а на самом деле сжимаются примерно в той же степени, что и твёрдые тела с кристаллической структурой), а также потенциальную энергию упругого (а если не повезёт — то и пластического, то есть необратимого) растяжения стенок трубы. Всё это приводит к тому, что давление в месте остановки стремительно возрастает, тем больше, чем выше была скорость жидкости и чем меньше её сжимаемость, а также чем выше жёсткость трубы. Это повышение давления и является гидравлическим ударом внезапно остановленной жидкости.
Фазы развития гидроудара
Как же развивается явление гидроудара? Рассмотрим самый простой пример — внезапное заполнение жидкостью пустой трубы постоянного сечения, погружённой на некоторую глубину. Один конец этой трубы закрыт жёсткой заглушкой, а другой свободно сообщается с окружающей жидкостью. Кстати, практически то же самое будет, если рассматривать резкое перекрытие установившегося потока в такой же трубе, только там будет отсутствовать первая фаза — заполнение пустой трубы, — а роль заглушки будет играть перекрывшая трубу заслонка.
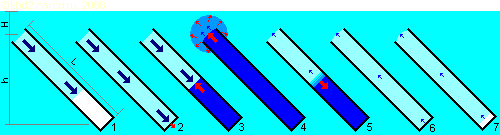 Схема возникновения гидравлического удара при заполнении жидкостью пустой трубы.
Голубым цветом обозначена внешняя среда с исходным давлением, светло-голубым — область пониженного давления, синим — область повышенного давления (зона гидроудара). Синие стрелки показывают перемещение вещества среды (жидкости), красные — перемещение границы зоны повышенного давления (без существенного перемещения вещества). H — глубина (напор) на входе трубы; h — перепад высот трубы, L — длина трубы от входа до заглушки. Цифрами обозначены фазы развития явления.
Таблица 1. Фазы развития гидравлического удара
| № фазы |
Название фазы |
Описание фазы |
| 1 |
Заполнение трубы |
Под действием внешнего давления жидкость заполняет трубу, при этом в соответствии с законом Бернулли её давление несколько меньше давления неподвижной среды вне трубы. |
| 2 |
Встреча с препятствием |
Жёсткая заглушка внезапно останавливает поток, который ударяется в неё. Однако практически вся жидкость в трубе ещё продолжает своё движение вперёд. |
| 3 |
Рост зоны повышенного давления |
Головная часть потока остановилась и её кинетическая энергия перешла в потенциальную энергию упругой деформации жидкости и стенок трубы, вызвав в этой области повышение давления. Но до «хвоста» потока это воздействие ещё не дошло, и там жидкость продолжает двигаться в прежнем направлении. Граница области повышенного давления (ударная волна) перемещается от заглушки ко входу трубы, при достаточной жёсткости трубы эта скорость практически равна скорости распространения упругих колебаний в среде, т.е. скорости звука в жидкости. |
| 4 |
Максимум повышенного давления |
Ударная волна достигла входа трубы и вышла в неподвижную среду. Поскольку внешняя среда неподвижна относительно стенок трубы, она уже не добавляет свою кинетическую энергию и не оказывает существенного сопротивления сжатой жидкости в трубе, и та начинает двигаться из зоны повышенного давления наружу. Кроме того, в свободной среде стенки трубы уже не ограничивают и не «фокусируют» ударную волну, так что она распространяется во все стороны, быстро теряя силу. Таким образом, достигнув входа трубы, ударная волна «рассеивается» и «гаснет». Более подробно этот момент рассмотрен ниже. |
| 5 |
Начало обратного движения |
Поскольку у входа в трубу давление относительно невысоко, сжатая жидкость двигается туда под действием повышенного давления внутри трубы. При этом потенциальная энергия упругой деформации снова превращается в кинетическую энергию, но движение уже направлено в обратную сторону. В результате граница зоны неподвижной жидкости под повышенным давлением перемещается от входа в трубу обратно к заглушке, оставляя у входа зону немного пониженного давления, в которой жидкость движется обратно ко входу трубы. Скорость перемещения этой границы в случае достаточно жёсткой трубы также равна скорости распространения упругих деформаций в среде, т.е. скорости звука в жидкости, однако перепад давления на границе не такой резкий, как при распространении ударной волны — зона границы существенно шире. Причиной этого являются особенности процесса рассеивания ударной волны у входа в трубу на предыдущей фазе.
При падении давления вся потенциальная энергия упругой деформации снова переходит в кинетическую энергию жидкости (за вычетом компенсации внешнего давления и неизбежных потерь, которые могут быть весьма малы), поэтому при сильных гидроударах скорость «разряженной» жидкости почти равна её скорости до остановки, только направлена теперь в сторону входа. |
| 6 |
Окончание сжатия |
В момент, когда граница зоны пониженного давления достигает заглушки, во всей трубе жидкость снова испытывает пониженное давление и движется обратно ко входу со скоростью, равной скорости потока в трубе в фазе 2. |
| 7 |
Фаза разрежения (отрыва) |
Двигаясь в сторону входа трубы, жидкость в силу инерции стремится оторваться от заглушки. Поэтому, если гидроудар был достаточно сильным, то возле заглушки образуется зона разрежения, где жидкость отсутствует и давление близко к нулю (именно вакуум, а не атмосферное давление). Однако жидкость, выходящая из трубы, движется не в пустоту, а в среду, представляющую собой ту же жидкость, только неподвижную. Сопротивление этой среды достаточно быстро затормозит движение жидкости к выходу и вместе с зоной разрежения возле заглушки вновь заставит жидкость двигаться от входа внутрь трубы, тем самым повторяя фазу 1 (естественно, уже с меньшей энергией, потери которой, как всегда, неизбежны).
При слабом гидроударе жидкости не удаётся оторваться от заглушки, однако всё равно давление существенно снижается относительно давления вне трубы (настолько, насколько оно повысилось в фазе сжатия). В этом случае выделяют фазы распространения отрицательной ударной волны (границы зоны с низким давлением) ко входу трубы и её возвращения обратно под действием внешнего давления, однако при сильном гидроударе с отрывом жидкости от заглушки появляется ещё и фаза «замирания». Впрочем, самостоятельное значение этих фаз не очень велико, поэтому все их я объединяю в одну фазу разрежения. Чуть ниже это рассмотрено более подробно. |
Факторы, влияющие на силу гидроудара
Эластичные стенки трубопровода значительно снижают силу гидроудара, достаточно легко увеличивая объём трубы или шланга в месте остановки жидкости. Если труба заполнена воздухом и по мере продвижения жидкости он не успевает покинуть трубу с нужной скоростью, это также способно предотвратить сильный гидроудар, поскольку в этом случае воздух играет роль пневматического амортизатора, так как по мере продвижения жидкости нарастает сжатие оставшегося воздуха, и он оказывает всё большее сопротивление движению жидкости, постепенно замедляя её. Именно эти принципы использует большинство устройств для защиты трубопроводов от гидроударов.
Следует чётко понимать, что эти факторы лишь растягивают процесс гидроудара во времени, хотя общая энергия гидравлического удара при этом остаётся прежней. Однако за счёт увеличения времени процесса, снижается его мощность, а значит, и максимальное давление, и максимальное усилие, воздействующее на стенки трубы. Но именно это и является целью защиты от гидроудара — ведь теперь трубу уже не разорвёт!
И, конечно, силу гидроудара снижает более плавное перекрытие потока и уменьшение рабочей скорости движения жидкости в трубе (если необходимо сохранить расход, то для этого придётся увеличить диаметр трубы — скорость уменьшится пропорционально увеличению площади её просвета).
Если же силу гидроудара надо увеличить, то тут рекомендации обратные — как можно более жёсткая (и прочная!) труба, как можно более резкое перекрытие потока и как можно больший разгон жидкости перед остановкой потока.
Особенности явления гидроудара
Гидроудар в силу своей природы имеет несколько существенных особенностей, о которых нельзя забывать.
Высокая скорость процесса
Прежде всего, следует учесть высокую скорость процесса. Поскольку скорость перемещения границ зон с различным давлением при высокой жёсткости трубы и заглушки определяется скоростью распространения упругих деформаций в жидкости, т.е. скоростью звука, всё происходит за очень короткое время.
Скорость звука в жидкостях обычно составляет порядка 1000...1500 м/с (для воды при 4°С — 1.435 км/с, при 45°С 1.51 км/с (максимум), при 100°С — 1.46 км/с), поэтому в трубе с водой длиной 15 метров процесс распространения ударной волны от заглушки до входа или обратно займёт примерно 10 миллисекунд. (Для сравнения: за это время тело, находящееся в покое, под действием ускорения свободного падения успеет набрать лишь скорость в 9.8 см/сек и пройти путь менее 5 сантиметров.) При более коротких длинах эти цифры пропорционально уменьшатся.
Это означает, например, что в горизонтальной трубе за такое время пустота в зоне отрыва не успеет сколько-нибудь существенным образом перераспределиться и останется «сконцентрированной» именно возле заглушки, а не превратится в относительно небольшое снижение уровня жидкости на значительной части длины трубы. Многие другие эффекты, скажем, испарение заметного количества жидкости с границы зоны отрыва в область разрежения и, как следствие, существенное повышение там давления, также не смогут проявиться в полной мере из-за краткости отпущенного им времени.
Условия отрыва жидкости. Сильные и слабые гидроудары
В фазе разрежения отрыв жидкости от заглушки происходит не всегда. Для этого скорость потока должна быть достаточно высокой, а стенки трубы — достаточно жёсткими, чтобы удар получился резким. Если удар окажется слишком слабым (или слишком плавным), то пустой области у заглушки не образуется, хотя в любом случае в фазе разрежения давление внутри трубы, в том числе непосредственно у заглушки, будет меньше, чем давление окружающей жидкости снаружи.
Для того, чтобы жидкость смогла оторваться от заглушки и появилась область отрыва, обратное давление (в идеале, без учёта потерь, равное максимальному повышению давления при сжатии) должно превышать давление среды снаружи. Таким образом, отрыв жидкости с образованием вакуума возможен при выполнении условия
ΔPуд > P0 + ΔPh + ΔPT (1),
где ΔPуд — максимальное повышение давления в фазе сжатия относительно внешнего давления; P0 — абсолютное внешнее давление в резервуаре возле входа в трубу (т.е. давление относительно вакуума, а не атмосферы над поверхностью жидкости); ΔPh — гидростатическая разность давлений между входом в трубу и заглушкой, если труба расположена не горизонтально; ΔPT — необратимые потери давления при сжатии и расширении жидкости и стенок трубы в фазах 2- 6.
Если пренебречь потерями, то для строго горизонтальной трубы критерий возникновения области вакуума будет ещё проще:
Может возникнуть вопрос: как же повышение давления при гидроударе может превысить давление на входе в трубу? Однако здесь нет парадокса, так как скачок давления зависит лишь от резкости остановки потока и набранной им к этому моменту кинетической энергии, поэтому жёсткая труба и малосжимаемая жидкость могут обеспечить сильный удар даже при не слишком высокой скорости потока.
Таким образом, гидроудары можно разделить на «сильные», когда образуется область вакуума в зоне отрыва, и «слабые», когда мощности удара для этого не хватает. При этом следует помнить, что речь именно о мощности удара, а не о его энергии, поскольку здесь определяющую роль играет резкость остановки.
Повторные циклы
Как уже было сказано выше, после фазы 7 (разрежения) снова следует фаза 1 — пустая (или разреженная) часть трубы снова заполняется жидкостью под давлением. В результате при гидроударе происходит своеобразный колебательный процесс, естественно, довольно быстро затухающий. При этом весьма важно знать, что же является главным фактором для возникновения повторного удара — разгон жидкости, заполняющей пустоту, возникшую при отрыве её от заглушки в фазе разрежения или упругая реакция внешней среды на возмущения, вызванные отбойным движением жидкости от заглушки ко входу в фазах 4–6.
Ответ на этот вопрос определяет, является ли отрыв жидкости от заглушки в фазе 7 необходимым условием возникновения повторных циклов или они будут иметь место даже если отрыва не происходит?
Посмотрим, как при гидроударе с течением времени изменяется давление возле заглушки.
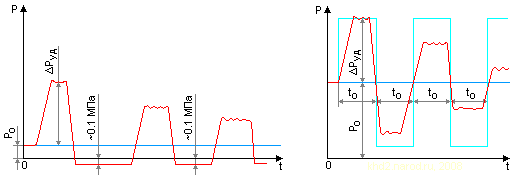 Изменение во времени давления возле заглушки при гидроударе.
Слева — сильный удар (с отрывом жидкости от заглушки), справа — слабый (без отрыва). Синей линией показан уровень исходного давления (до начала гидроудара), голубой линией — идеальный характер изменения давления при отсутствии потерь энергии. P0 — давление свободной среды возле входа в трубу; ΔPуд — максимальное повышение давления при гидроударе; t0 — длительность этапа при слабом гидроударе. По материалам сайта gidravl.narod.ru.
На рисунке видно, что при сильном гидроударе (слева) в фазе отрыва давление падает практически до нуля, т.е. образуется вакуум (0.1 МПа ~ 1 атм, давление измерялось относительно атмосферного, поэтому показания в –1 атм как раз и соответствуют абсолютному нулю давления). Однако это не слишком снижает энергию повторных гидроударов, более того, характер их постепенного ослабления не отличается от аналогичного ослабления при слабом гидроударе, показанном на рисунке справа.
При слабом гидроударе (без отрыва жидкости), фазы сжатия и разрежения имеют одинаковую длительность t0, обусловленную временем «путешествия» ударной волны от заглушки ко входу трубы и обратно. В этом случае возмущения не выходят в резервуар сколько-нибудь далеко от входа трубы, и период этих колебаний полностью определяется длиной трубы и скоростью ударной волны.
При сильном гидроударе обратным ходом (отбойной волной) жидкость выбрасывается из трубы с большой силой, и она выходит в резервуар достаточно далеко от входа в трубу, «расталкивая» уже находившуюся там жидкость. В результате этого в трубе возле заглушки освобождается место для зоны отрыва, однако и сила повторного удара обусловлена не только разрежением жидкости в трубе, но и возмущённой жидкостью в резервуаре вокруг входа в трубу. Поэтому повторный удар получается сильным, однако «затишье» между ударами существенно больше длительности каждого удара, поскольку ударная волна выходит далеко за пределы трубы, и этот путь требует дополнительного времени. По мере снижения силы повторных ударов интервал между ними сокращается, и когда скачок давления при очередном повторном гидроударе ΔPуд становится равным давлению вне трубы P0, сравнивается с t0 и в дальнейшем уже не уменьшается.
С точки зрения математики можно сказать, что в каждом цикле гидроудара площади положительного и отрицательного отклонения от уровня давления P0 на графике P(t) должны быть равны, поскольку они пропорциональны энергии, а без учёта потерь энергия стадии сжатия и стадии разрежения должна быть одинаковой. И, так как разрежение не может быть отрицательным, то в случае возникновения отрыва это условие соблюдается за счёт увеличения длительности фазы разрежения. Если же отрыва не возникает, то энергия «регулируется» амплитудой скачка давления, так как теперь «вакуумное ограничение» на стадии разрежения перестаёт действовать.
Таким образом, пренебрегая потерями и считая фронты нарастания и спада давления достаточно резкими (близкими к вертикальным), можно записать условие соотношения длительностей стадий сжатия и разрежения возле заглушки в следующем виде:
(P0 – Pс) · tсз = (Pр – P0) · tрз или ΔPс · tсз = –ΔPр · tрз (3),
где P0 — исходное давление до начала гидроудара; Pс — давление на стадии сжатия; tcз — длительность стадии сжатия возле заглушки; Pр — давление на стадии разрежения; tpз — длительность стадии разрежения возле заглушки; ΔPс — изменение давления на стадии сжатия; ΔPр — изменение давления на стадии разрежения.
Размер имеет значение
С увеличением размеров трубы сила гидроудара значительно возрастает, причём для одного и того же давления у входа в трубу этот рост обычно круче линейной зависимости. Здесь мы рассмотрим качественные причины такого поведения (количественные результаты автоматически следуют из расчётов, приведённых в следующих разделах этой страницы).
Дело в том, что энергия гидроудара определяется его длительностью, зависящей от длины и жёсткости трубы, и мощностью, которая прямо зависит от скачка давления, в свою очередь линейно зависимого от скорости потока в момент остановки. Поэтому при той же скорости потока скачок давления будет тем же, но длительность гидроудара, а значит и его общая энергия, возрастут в соответствии с увеличением длины трубы.
Однако при увеличении линейных размеров масса (и, следовательно, кинетическая энергия при той же скорости) возрастает пропорционально объёму, т.е. кубу их изменения, а потери на трение о стенки трубы — пропорционально площади соприкосновения, то есть квадрату изменения размеров. Таким образом, удельные потери энергии на трение на единицу массы жидкости уменьшаются, и потому при том же движущем усилии (внешнем давлении) скорость потока возрастает, а стало быть, увеличивается и скачок давления в момент остановки.
В результате при одном и том же внешнем давлении мы получаем сильный гидроудар в большой трубе и слабый — в маленькой. При этом слишком большое удлинение трубы без увеличения её диаметра также ослабит гидроудар за счёт того, что возрастающее гидравлическое сопротивление снизит скорость потока к моменту остановки. Отсюда следует вывод, что имеется некоторая оптимальная (или, может быть, наоборот — фатальная) длина трубопровода, при которой гидроудар имеет максимальную силу. При меньшей длине поток не успевает разогнаться до максимальной скорости либо длительность гидроудара получается слишком маленькой, при большей — гидравлическое трение отбирает слишком много энергии у движущегося потока, снижая его скорость до «безопасных» величин. Кроме того, если при увеличении диаметра трубы толщина её стенок не увеличится, то жёсткость, а следовательно, скорость ударной волны и скачок давления при гидроударе снижаются. Правда, на столько же возрастает его длительность, — так что общую энергию гидроудара снижение толщины стенок не уменьшает, а вот шансы разрыва трубы увеличиваются!
Для слишком узких трубок большое значение начинают играть поверхностные эффекты, в том числе поверхностное натяжение. Все они препятствуют разгону потока и потому также снижают силу гидроудара. Чтобы получить в капиллярной трубке сколь-нибудь заметный гидравлический удар, надо сильно постараться!
Расчёт параметров гидравлического удара
Наиболее интересны два параметра гидроудара — во-первых, его мощность (либо степень повышения давления) и, во-вторых, длительность стадий сжатия (фазы 2-6) и разрежения (фаза 7), вместе с мощностью определяющих общую энергию гидравлического удара.
Расчёт повышения давления при гидроударе. Формула Жуковского
Повышение давления при гидравлическом ударе рассчитывается по формуле Жуковского:
где ΔPуд — скачок давления; ρ — удельная плотность жидкости; Δv — произошедшее изменение скорости (при полной остановке — скорость потока перед остановкой); с — скорость распространения ударной волны.
В свою очередь, скорость распространения ударной волны определяется по формуле:
c = 1 / √(ρ · β + 2 · ρ · r / (δ · E)) (5),
где c — скорость ударной волны; √ — операция извлечения квадратного корня; ρ — удельная плотность жидкости; β — сжимаемость жидкости; r — внутренний радиус трубы; δ — толщина стенок трубы; E — модуль упругости материала трубы ( модуль Юнга).
Следует отметить, что скачок давления при гидравлическом ударе не зависит от исходного давления, заставившего двигаться жидкость по трубе, а зависит только от набранной ею скорости. Это значит, что разгон жидкости относительно высоким давлением в течение короткого времени можно заменить более длительным разгоном под воздействием более низкого давления. Впрочем, бесконечно снижать разгоняющее давление не удастся: во-первых, в реальных условиях напор низкого давления уже при не слишком большой скорости потока весь уйдёт на компенсацию гидравлического трения; во-вторых, даже для сверхтекучей жидкости действует ограничение на максимальную скорость, которой поток может достичь при заданном напоре на входе трубы в соответствии с уравнением Бернулли.
Тем не менее, именно это обстоятельство позволяет гидравлическим таранам поднимать жидкость на высоту, во много раз превышающую приводящий их в действие перепад уровней.
Расчёт длительности стадий сжатия и разрежения у заглушки
Расчёт длительности стадий сжатия и разрежения будем проводить в предположении, что длина трубы, а следовательно, и время распространения гидроудара по ней, намного больше времени рассеивания ударной волны у входа в трубу. Это справедливо в большинстве случаев, поскольку обычно длина трубы превышает её диаметр в десятки, сотни, а то и тысячи раз. Однако для коротких труб, длина которых сравнима с их диаметром, нельзя не учитывать механизм рассеяния ударной волны у её входа, поскольку в этом случае он может заметно повлиять на длительность стадии сжатия.
Длительность стадии сжатия
Как мы выяснили немного выше, длительность стадии сжатия не зависит от силы гидроудара, а определяется лишь временем распространения ударной волны по трубе, поэтому у заглушки она длится время, необходимое для прохода ударной волны по трубе «туда» и «обратно»:
где tcз — длительность стадии сжатия возле заглушки; L — длина трубы от входа до заглушки; с — скорость распространения ударной волны, вычисляемая по формуле (5). Длительность стадии разрежения
При слабых гидравлических ударах, когда не выполняется условие (1) и отрыва жидкости от заглушки с образованием области вакуума не возникает, длительность стадии разрежения равна длительности стадии сжатия, вычисляемой по формуле (6).
Однако если силы гидроудара достаточно для возникновения отрыва жидкости от заглушки и образования области вакуума, то есть условие (1) выполнено, длительность стадии разрежения возрастает в соответствии с соотношением (3) и с учётом формулы (4) она должна рассчитываться как
tрз = tcз · ΔPуд / P0 = 2 · L · ρ · v0 / P0 (7),
где tpз — длительность стадии разрежения возле заглушки; tcз — длительность стадии сжатия возле заглушки; ΔPуд — повышение давления на стадии сжатия при гидроударе, вычисляемое по формуле Жуковского; P0 — исходное давление до начала гидроудара (давление вне трубы); L — длина трубы от входа до заглушки; ρ — удельная плотность жидкости; v0 — скорость потока перед остановкой.
Таким образом, длительность стадии разрежения при слабом гидроударе помимо длины трубы зависит лишь от скорости ударной волны, а при сильном — уже от его силы.
Расчёт длительности стадий сжатия и разрежения в произвольном месте трубы
Картина изменения давления в произвольном месте трубы несколько сложнее, чем показанная на предыдущем рисунке возле заглушки.
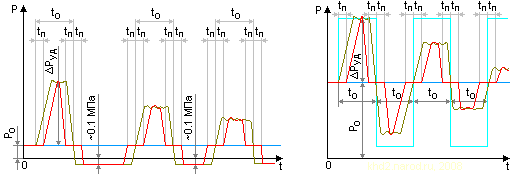 Изменение давления со временем в произвольном месте трубы при гидроударе.
Слева — сильный удар (с отрывом жидкости от заглушки), справа — слабый (без отрыва). Красным показано изменение давления в середине трубы, жёлто-серым — возле заглушки; синяя линия показывает уровень исходного давления (до начала гидроудара), голубая — идеальный характер изменения давления у заглушки при отсутствии потерь энергии. P0 — давление свободной среды возле входа в трубу; ΔPуд — максимальное повышение давления при гидроударе; t0 — длительность этапа при слабом гидроударе; tП — длительность «полочки».
Здесь появляются «полочки», уменьшающие длительности экстремальных давлений (как пониженного, так и повышенного) относительно длительности каждого этапа возле заглушки. Они связаны с задержкой, неизбежной при распространении до интересующего нас места трубы возникающей возле заглушки зоны экстремального давления. Очевидно, что по мере приближения к заглушке эти «полочки» будут уменьшаться и совершенно исчезают возле заглушки. Наоборот, по мере приближения ко входу в трубу из резервуара они нарастают, пока в сумме не станут равны tсз (оно же t0 на рисунках). Таким образом, возле входа в трубу длительность стадии сжатия становится ничтожной, а вот длительность стадии разрежения при условии сильного удара с отрывом жидкости от заглушки будет оставаться вполне заметной.
Длительность «полочки» определяется расстоянием от заглушки и скоростью распространения ударной волны:
где tп — длительность «полочки» (стадии нормального давления); l — расстояние по трубе до заглушки; с — скорость распространения ударной волны, вычисляемая по формуле (5).
Таким образом, длительность стадий сжатия и разрежения в произвольном месте трубы будет рассчитываться по формулам
где tc и tр — длительности стадий сжатия и разрежения в произвольном месте трубы; tcз и tрз — длительности стадий сжатия и разрежения возле заглушки, вычисляемые по формулам (6) и (7) соответственно; tп — длительность «полочки» (стадии нормального давления) в данном месте трубы, вычисляемая по формуле (8).
Не следует думать, что в силу конечного времени нарастания и спада давления (неидеальности фронтов) максимальные усилия на стенки трубы возле её входа будут меньше, чем возле заглушки. Время воздействия максимального давления у входа действительно будет мизерным, но сам спад максимального давления начинается уже вне трубы — в зоне ускорения жидкости. И неидеальность фронта спада формируется именно там — вне трубы.
Наконец, следует отметить, что разрежение, вплоть до практически полного отсутствия давления при сильном гидроударе, отнюдь не означает, что на этой стадии жидкость покидает всю трубу. Это лишь означает, что жидкость перестаёт давить на её стенки. Реально пустота образуется только в зоне отрыва возле заглушки — там же, где возник гидроудар при внезапном перекрытии потока.
Расчёт ускоряющегося потока
Сила гидравлического удара прямо зависит от скорости, которую успел набрать останавливаемый поток. Достаточно определённо о скорости потока можно сказать только в одном случае — при резком перекрытии установившегося потока. Однако во многих случаях поток под воздействием внешнего давления (или, что то же самое, перепада уровней) периодически набирает некоторую скорость, после чего резко перекрывается, а затем цикл повторяется снова — таков, скажем, принцип работы гидравлических таранов. Этот же процесс имеет место при повторных циклах гидроудара независимо от того, был ли вызван первичный гидроудар перекрытием установившегося или ускорявшегося потока. Поэтому возникает необходимость определить следующие взаимосвязанные величины:
- максимальную скорость, которую изначально покоящаяся жидкость под воздействием внешнего давления может набрать при заполнении трубы;
- время, за которое на этом расстоянии поток наберёт заданную скорость (конечно, не превышающую максимально возможной);
-
скорость, которую поток может достичь, имея заданное расстояние для разгона.
При рассмотрении будем предполагать, что поток начинает заполнять горизонтальную пустую трубу, среда внутри которой не оказывает ему сколько-нибудь заметного сопротивления. Кроме того, давление в резервуаре на уровне входа в трубу также будем считать постоянным (это соответствует ситуации, когда объём резервуара намного больше заполняемого объёма трубы, либо такая неизменность давления обеспечивается специальными техническими средствами).
Расчёт сначала проведём без учёта потерь на гидравлическое трение (для сверхтекучей жидкости), а затем попробуем учесть потери.
Где ускоряется жидкость?
Прежде всего следует выяснить, где происходит ускорение жидкости — в трубе или вне её? Уравнение непрерывности даёт однозначный ответ: внутри трубы неизменного сечения скорость потока также неизменна, а следовательно, всё ускорение происходит в резервуаре перед трубой! В этом легко убедиться, наблюдая за сливом воды из ванны — «воронка» над сливным отверстием обусловлена именно зоной ускорения воды, находящейся в объёме самой ванны, а в сливной трубе скорость воды уже не меняется. Поэтому и энергия гидравлического удара обусловлена всем объёмом воды, двигающейся в трубе с одной и той же скоростью.
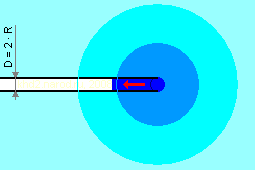 Вовлечение заполняющей трубу жидкости в движение вне трубы.
Более насыщенным цветом показаны области с большей скоростью. Градации показаны условно, нарастание скорости происходит плавно.
Давайте определим форму границы области, на которой скорость жидкости меньше скорости в трубе на одну и ту же величину (форму эквискоростной поверхности). Поскольку вне трубы жидкость стремится к её входу со всех сторон в равной степени (давление-то везде одинаково), логично предположить, что при отсутствии каких-либо дополнительных направляющих граница этой области ускорения вокруг входа в трубу имеет сферическую форму. Впрочем, вблизи от входа трубы она будет несколько отличаться от сферической из-за того, что жидкость «сзади» от входа испытывает гидравлическое трение о стенки трубы и, к тому же, прежде чем попасть внутрь, ей необходимо поменять направление, то есть ей труднее попасть в трубу, чем той, что находится напротив входа и практически не меняет направление движения вплоть до попадания внутрь трубы. Однако по мере удаления от входа влияние этих факторов ослабевает и форма эквискоростной поверхности будет всё более приближаться к сферической.
Следует отметить ещё один фактор, влияющий на форму эквискоростной поверхности — это градиент давления. Если он значителен (это имеет место возле поверхности, когда при относительно небольшом увеличении глубины давление может изменяться в разы), то такая поверхность приобретает яйцеобразную форму острым концом вверх, а уровню входа трубы соответствует самая широкая часть этого «яйца». На большой глубине, где при той же разности уровней давление меняется лишь на малые доли процента, форма эквискоростной поверхности будет практически неотличима от идеальной сферы.
Остаётся определить закон, по которому меняется скорость жидкости во внешней среде по мере удаления от входа в трубу. Ответ определяется всё тем же уравнением непрерывности: скорость обратно пропорциональна площади сечения потока, а стало быть, квадрату расстояния от входа в трубу (при строгом расчёте из площади сферы необходимо вычесть площадь сегмента, соответствующего внешнему диаметру трубы, однако уже на расстоянии полутора радиусов от центра входа в трубу его доля составляет лишь немногим более 10%, в двух радиусах — около 7%, а в пяти радиусах — всего 1%).
Гашение ударной волны
Поскольку жидкость разгоняется перед входом в трубу, то, когда в результате гидроудара жидкость в трубе остановилась, вынуждена остановиться и уже набравшая некоторую скорость жидкость возле входа в трубу. Эта остановка вызывает повышение давления вокруг входа, что часто интерпретируется как «выход ударной волны из трубы». Однако повышение давления прямо пропорционально скорости останавливаемой жидкости, а вне трубы эта скорость падает обратно пропорционально квадрату расстояния до входа. Поэтому уже в 10 радиусах трубы от её входа скачок давления при гидроударе составит лишь 1% от его силы в самой трубе — это выглядит как «затухание» ударной волны при выходе её из трубы.
Жидкость в трубе начинает двигаться наружу сразу, как только ударная волна вышла из трубы, поскольку давление сразу становится меньше давления в трубе, хотя и превышает давление невозмущённой внешней жидкости. Однако перепад давлений пока не так велик, и поэтому жидкость движется ещё не так быстро. Затем давление вне трубы быстро падает, и скорость движения жидкости наружу также быстро нарастает. Тем не менее, этот процесс обуславливает принципиальную неидеальность фронта падения давления, начинающего движение от входа к заглушке — он не может быть идеально скачкообразным даже теоретически! На рисунке в фазе (5) это показано как размытость границы падения давления.
Наконец, следует напомнить, что все описанные здесь процессы присходят очень быстро. Если гидроудар был достаточно слабый и отрыва жидкости от заглушки не произошло, то для трубы диаметром в несколько сантиметров время гашения ударной волны и формирование обратного фронта измеряется не милли-, а микросекундами!
Кстати, при обратном движении на стадии отбоя торможение выбрасываемой из трубы жидкости также происходит вне её пределов — в объёме резервуара возле входа. В случае сильного обратного движения со значительным отрывом жидкости от заглушки несферичность зоны торможения более выражена за счёт изначального присутствия направленного скоростного напора, и вблизи от входа трубы она, скорее, напоминает «факел», чем сферу. При этом непосредственно у стенок трубы возле входа возможна эжекция (подсос) жидкости в направлении выброса, то есть к срезу трубы, а не от него. Однако по мере торможения и удаления от входа форма эквискоростной поверхности при торможении выброса во внешней среде опять-таки приближается к сферической.
Расчёт скорости заполняющего трубу потока для сверхтекучей жидкости
Выяснив, что жидкость ускоряется вне трубы, а внутри неё скорость потока одинакова, можно переходить к расчётам скорости.
Сначала рассмотрим внезапное заполнение абсолютно пустой трубы. Условно разобьём непрерывный поток на маленькие порции, мысленно нарезав его поперёк движения на тоненькие «ломтики».
В соответствии с уравнением Бернулли, когда первая порция жидкости ринется в трубу, при разгоне жидкости с неизменным гравитационным потенциалом (в горизонтальной трубе) всё давление должно будет перейти в скоростной напор:
где ρ — удельная плотность жидкости; v — скорость потока; –ΔP — потери давления, перешедшие в скоростной напор.
При этом со стороны трубы жидкости ничего не препятствует — труба пуста, поэтому первая порция набирает максимальную скорость практически мгновенно. За ней устремляется следующая порция, на которую сзади действует такое же давление, и спереди её также ничто не сдерживает — ведь первая порция уже унеслась вперёд с максимально возможной скоростью! Поэтому и вторая порция на входе в трубу набирает максимально возможную скорость. То же самое происходит и с третьей, и с последующими порциями. Конечно, в реальности они ускоряются более плавно, чем самое начало потока, но всё это ускорение, как мы выяснили чуть выше, происходит перед входом в трубу, внутри же трубы, начиная от самого её входа, заполняющий поток движется с максимально возможной скоростью, определяемой давлением на входе в трубу:
где vМ — максимальная скорость потока; √ — операция извлечения квадратного корня; ρ — удельная плотность жидкости; P — давление возле входа в трубу. Мы получили вариант известной формулы Торричелли для определения скорости свободно истекающей жидкости.
Теперь предположим, что в трубе возле входа уже было некоторое количество жидкости, которая, к тому же, уже двигалась с некоторой скоростью. Тогда по закону Бернулли со стороны жидкости вне трубы на неё будет действовать сила
F = (P0 ± ρ · v2 / 2) / (π · R2) (13),
где F — сила от внешнего давления, воздействующая на жидость в трубе; P0 — внешнее давление возле входа в трубу; ρ — удельная плотность жидкости; v — скорость жидкости в трубе; R — внутренний радиус трубы; ± — определяется направлениями давления и скорости жидкости: если они совпадают, следует вычитать, а если направлены встречно — складывать.
Соответственно, ускорение жидкости будет определяться этой силой и массой жидкости в трубе:
a = F / m = ((P0 ± ρ · v2 / 2) / (π · R2)) / (ρ / (x · π · R2)) = (P0 / ρ ± v2 / 2) / x (14),
где a — ускорение жидкости в трубе под воздействием внешнего давления; P0 — внешнее давление (возле входа в трубу); ρ — удельная плотность жидкости; v — скорость жидкости в трубе; R — внутренний радиус трубы; x — текущее заполнение трубы, т.е. расстояние от начала потока до входа в трубу; ± — векторное сложение давления и скоростного напора, определяемое направлениями давления и скорости жидкости: если они совпадают, следует вычитать, а если направлены встречно — складывать.
Проанализируем только что полученную формулу для ускорения.
-
Если жидкость движется навстречу внешнему давлению, внешнее давление тормозит её, суммируя своё воздействие со скоростным напором жидкости. Эта ситуация имеет место во время обратного хода жидкости при отбое гидроудара в фазах 5 — 7 (пока обратное движение не остановится).
-
Если жидкость в трубе покоится или движется в ту же сторону, куда действует внешнее давление, но скорость её меньше максимальной vM (12), внешнее давление ускоряет её движение внутрь трубы и тем сильнее, чем медленнее движется жидкость. Эта ситуация соответствует фазе 1 при повторных циклах сильного гидроудара (с отрывом).
-
Если жидкость в трубе движется в ту же сторону, куда действует внешнее давление, со скоростью, равной максимальной vM (12), ускорение отсутствует. Эта ситуация соответствует рассмотренному чуть выше заполнению пустой трубы, когда скорость заполнения неизменна и максимальна.
-
Наконец, если жидкость в трубе движется в ту же сторону, куда действует внешнее давление, но её скорость превышает vM (12), внешнее давление не может ускорить жидкость в трубе, а новая жидкость заполняет трубу как пустую со скоростью vM. Впрочем, для создания такой ситуации надо приложить особые усилия и проявить немало изобретательности.
В соответствии с формулой (14) скорость потока при заполнении трубы на расстояние x от входа в трубу будет равна
v(x) = lx∫ a(x) dx = lx∫ ((P0 / ρ ± v(x)2 / 2) / x) dx (15),
где v(x) — скорость жидкости в трубе с учётом заполнения трубы; l — начальное заполнение трубы от её входа; x — текущее заполнение трубы от её входа; a(x) — ускорение жидкости в трубе под воздействием внешнего давления с учётом заполнения трубы; P0 — внешнее давление (возле входа в трубу); ρ — удельная плотность жидкости.
Итак, при попытке рассчитать скорость аналитическими методами мы сталкиваемся с необходимостью брать интеграл функции от самой себя. Это обусловлено тем, что разгон жидкости в трубе относится к неустановившимся («нестационарным») процессам, развитие которых прямо определяется состоянием их важнейших параметров на предыдущем этапе. Теперь понятно, почему теория гидравлического удара так долго находилась лишь на уровне качественного описания явления, а практические расчёты выполнялись на основании опытных данных и эмпирических формул, подходящих только для узкого диапазона условий. Однако получившаяся ситуация не является препятствием для численных методов решения задач, а с учётом возможностей современных компьютеров использование численных методов не представляет проблемы. К тому же для приближения к реальности необходимо учесть и гидравлическое трение, расчёт которого в аналитической форме, мягко говоря, весьма затруднителен...
Расчёт скорости заполняющего трубу потока с учётом гидравлического трения
В реальности для получения заметного гидроудара скорость потока перед его остановкой должна быть достаточно большой, так что при расчёте скорости нельзя не учитывать потери от гидравлического трения. К сожалению, расчёты гидравлического трения основаны на эмпирических закономерностях, каждая из которых действует в своём диапазоне скоростей. Поэтому решать такую задачу с учётом всех нюансов наиболее удобно с помощью численных методов. В общем виде её решение заключается в учёте в формуле (14) потерь на гидравлическое трение PT:
a = ((P0 ± PT) / ρ ± v2 / 2) / x (16).
Как и прежде, знак «±» указывает на векторное сложение внешнего давления, скоростного напора и гидравлического трения. Если движение жидкости направлено от входа трубы — по действию внешнего давления, — то внешнее давление стремится ускорить поток, но скоростной напор нейтрализует часть этого давления, а гидравлическое трение тормозит поток. Поэтому трение и скоростной напор следует вычитать. Если же движение жидкости направлено ко входу трубы (стадия отбоя — отрицательная скорость), остановить её совместно стремятся все три фактора. Поэтому пока жидкость движется вспять, нужно всё суммировать.
Поскольку расчёты гидравлического трения обычно выполняются как расчёт потерь напора HT, они переводятся в потери давления через плотность ρ и ускорение свободного падения g как PT = HT · g · ρ. Поэтому текущее ускорение с учётом потерь на трение следует рассчитывать по формуле
a = (P0 / ρ ± HT · g ± v2 / 2) / x (17),
Используя для расчёта потерь в круглой трубе универсальную формулу Вейсбаха-Дарси, получаем
a = (P0 / ρ ± v2 / 2) / x ± λ · v2 / (2 · D) = P0 / (ρ · x) ± (v2 / 2) · (1 / x + λ / D) (18),
где a — ускорение жидкости в трубе под воздействием внешнего давления; P0 — внешнее давление на уровне входа в трубу; ρ — удельная плотность жидкости; v — скорость жидкости в трубе; x — текущее заполнение трубы, т.е. расстояние от «головы» потока до входа в трубу; λ — безразмерный коэффициент гидравлического трения; D — внутренний диаметр трубы; ± — векторное сложение давления и скоростного напора, определяемое направлениями давления и скорости жидкости: если они совпадают, следует вычитать, а если направлены встречно — складывать.
Тем не менее, даже рассматривая влияние гидравлического трения лишь с точки зрения качественной оценки, можно сделать важный вывод. Если в начале разгона потока труба частично заполнена жидкостью, после достижения определённой длины заполненного участка, зависящей от внешнего давления и параметров трубы и жидкости, скорость потока перестанет повышаться и начнёт снижаться из-за того, что потери напора на трение превысят напор от внешнего давления. Поэтому слишком длинный пробег снизит силу гидроудара.
При заполнении пустой трубы скорость потока из-за трения начнёт снижаться сразу с начала заполнения. Однако это не значит, что для получения максимального гидроудара оптимальная длина пустой трубы должна быть как можно меньше: ведь чем меньше длина трубы, тем меньше длительность гидроудара, а следовательно, и его энергия, и его воздействие на стенки этой трубы. В предельном случае при нулевой длине трубы длительность гидроудара также нулевая, поэтому каким бы теоретически мощным он бы ни был, на практике вообще ничего произойти не может — ведь его энергия будет равна нулю!
К сожалению, даже приблизительные количественные оценки возможны только после выполнения необходимых расчётов с помощью специальной программы. В принципе, для написания такой программы можно использовать и Visual Basic из Excel, но он не очень удобен для решения подобных задач, хотя вся математика сводится к формуле (18) и расчёту коэффициента гидравлического трения. Поэтому была написана специальная программа. Результаты расчёта для заполнения пустых труб разного диаметра водой с различным напором приведены на отдельной странице.
Особые случаи
Теперь рассмотрим особые случаи гидроудара, когда условия существенно отличаются от рассматриваемых до сих пор «идеально-лабораторных». Наиболее часто встречающиеся отличия можно свести к следующим случаям.
-
Поток заполняет трубу, которая предварительно уже была частично заполнена жидкостью.
-
Поток сталкивается не с твёрдой неподвижной заглушкой, а с другим потоком жидкости, который может двигаться ей навстречу («лобовое столкновение») или в ту же сторону (новый поток догоняет и «подталкивает» предыдущий).
-
Гидроудар происходит с утечками жидкости из трубы, например, при неполном перекрытии трубы заслонкой или заглушкой, либо в трубе, где имеются дополнительные отверстия помимо входа, через который вливается поток.
Гидроудар в частично заполненной трубе
Нередко труба, в которую устремился поток, вызвавший гидроудар, бывает уже частично заполнена жидкостью — неподвижной или движущейся в ту или другую сторону. Рассмотрим два крайних случая — гидроудар в частично заполненной горизонтальной трубе, где жидкость равномерно распределена по её длине, и гидроудар в вертикальной трубе, где жидкостью уже заполнена часть трубы возле заглушки.
Рассматривая эту ситуацию в общем, можно сказать, что энергия гидроудара по сравнению с заполнением пустой трубы уменьшается в число раз k, равное
k = VП / VТ = (VТ — VЖ) / VТ (19),
где VП — незаполненный внутренний объём трубы; VT — весь внутренний объём трубы; VЖ — объём жидкости в трубе до начала заполнения её потоком.
Соответственно сила гидроудара, определяемая интегральной скоростью всей жидкости в трубе, уменьшится в √k, то есть пропорционально квадратному корню от отношения незаполненного объёма к общему объёму трубы.
Однако это утверждение полностью применимо лишь к повторным циклам такого гидроудара. Что же касается первого цикла, и прежде всего его стадии сжатия (первичного удара), то хотя за весь период в общем его энергетика будет соответствовать формуле (19), при внимательном рассмотрении возникают существенные нюансы, зависящие, в том числе, и от того, сосредоточена ли уже находящаяся в трубе жидкость в одном её конце (вертикальное положение) или равномерно распределена по всей её длине (горизонтальное положение).
Гидроудар в частично заполненной горизонтальной трубе
Предположим, что горизонтальная труба равномерно по всей длине заполнена на некоторую высоту неподвижной жидкостью. Когда такая труба вдруг начинает заполняться дополнительным потоком жидкости, он «сминает» ту жидкость, что уже была в трубе. Однако, пока в трубе есть свободное место, эта жидкость не оказывает жёсткого сопротивления, а «подчиняется», под действием напора потока повышая свой уровень и набирая скорость в направлении заполняющего потока. И только когда свободного места в трубе не остаётся, сопротивление становится жёстким и происходит гидроудар.
 Движение потока в частично заполненной горизонтальной трубе.
Более насыщенным цветом показаны области с большей скоростью. Градации показаны условно, нарастание скорости происходит плавно.
Нарастание скорости неподвижной жидкости происходит плавно. Сначала она преимущественно движется вверх (уровень поднимается), затем начинает увеличиваться горизонтальная составляющая, которая к моменту поднятия уровня до верха трубы становится равной скорости потока у входа в трубу. Поэтому можно сказать, что по мере приближения потока вектор скорости микрообъёма жидкости, находившейся в трубе, меняет своё направление с вертикального на горизонтальное, одновременно возрастая по абсолютной величине от нуля до скорости на входе в трубу.
С энергетической точки зрения, заполняющий поток вынужден терять свою энергию как на подъём уровня, так и на разгон уже имевшейся в трубе жидкости. Кроме того, через вход в трубу попадёт меньшее количество двигающейся жидкости, обладающей кинетической энергией, поскольку часть объёма трубы уже занята изначально покоящейся жидкостью. А энергия гидроудара определяется именно суммарной энергией всей жидкости находящейся в трубе в момент его начала.
Поэтому энергия гидроудара E будет равна
E = (VT — VЖ) · ρ · v2 / 2 (20),
где VT — весь внутренний объём трубы; VЖ — объём жидкости в трубе до начала заполнения её потоком; ρ — плотность жидкости; v — скорость заполняющего трубу потока.
Если жидкость в трубе уже двигалась, при расчёте потерь энергии заполняющим потоком это необходимо учесть. Здесь важно определить, из-за чего возникает основной гидравлический удар — из-за столкновения двух потоков жидкости или из-за столкновения общего потока с жёсткой заглушкой. В первом случае при встречном движении надо прибавлять, а при попутном вычитать скорость уже имеющейся в трубе жидкости из скорости заполняющего потока, во втором случае — наоборот.
Таким образом, гидравлический удар в горизонтальной трубе, которая предварительно уже частично заполнена, будет слабее, чем при заполнении пустой трубы.
Гидроудар в частично заполненной вертикальной трубе
Рассмотрим развитие гидроудара в вертикальной трубе, часть которой возле заглушки уже заполнена неподвижной жидкостью. Случай, когда жидкостью заполнена часть трубы возле входа, рассмотрен выше и описывается формулами (13) (для сверхтекучей жидкости) и (16)–(18) (с учётом гидравлического трения).
Когда поток сталкивается с неподвижной жидкостью возле заглушки, гидроудар возникает немедленно и распространяется в обе стороны — к заглушке и ко входу в трубу. При этом его сила (скачок давления) в соответствии с формулой Жуковского определяется лишь скоростью перед остановкой. Но зато длительность, а, следовательно, и полная энергия, определяется геометрией, то есть расстояниями от места столкновения до заглушки и до входа в трубу.
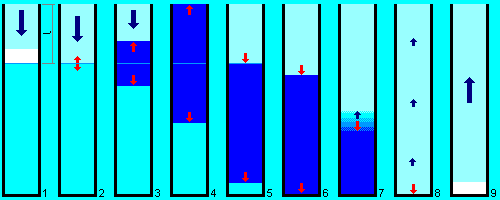 Схема развития гидравлического удара при заполнении потоком уже частично заполненной жидкостью вертикальной трубы.
Голубым цветом обозначена внешняя среда с исходным давлением, светло-голубым — область пониженного давления, синим — область повышенного давления (зона гидроудара). Синие стрелки показывают перемещение вещества среды (жидкости), красные — перемещение границы зоны повышенного давления (без существенного перемещения вещества). Светло-синяя линия отмечает исходный уровень неподвижной жидкости на расстоянии l от входа в трубу. Цифрами обозначены этапы развития процесса.
Разберём этапы развития этого процесса более подробно (в скобках указаны соответствующие цифры на рисунке). Заполняющий трубу поток (этап 1) натыкается на неподвижную жидкость. Поскольку деваться ей некуда, она сразу оказывает жёсткое сопротивление вновь прибывшей жидкости и останавливает её. Поэтому в месте столкновения кинетическая энергия потока сразу начинает переходить в потенциальную энергию упругой деформации, что сопровождается повышением давления — в месте столкновения возникает гидравлический удар (этап 2). Ударная волна от места удара начинает распространяться в обе стороны — как по набегающему потоку, останавливая всё новые его части, так и по неподвижной жидкости, сжимая её (этап 3). Впрочем, благодаря малой сжимаемости жидкостей при таком сжатии вещество почти не перемещается, поэтому неподвижная жидкость фактически остаётся там же, где была до начала гидроудара. Через какое-то время фронты сжатия, движущиеся в разные стороны, достигнут заглушки и выхода из трубы. Когда фронт сжатия достигнет заглушки, не произойдёт ничего, а вот когда фронт сжатия достигнет входа в трубу, ударная волна выйдет в среду и начнёт рассеиваться (этап 4), также как и в фазе (4) «классического» гидроудара.
Затем граница области сжатия начнёт откатываться внутрь трубы (этап 5 здесь и фаза (5) «классического» гидроудара). Однако пока передний фронт зоны сжатия ещё не достиг заглушки, сильного обратного движения жидкости за задним фронтом сжатия нет. Это обусловлено тем, что импульс исходного потока продолжает распространяться к заглушке до тех пор, пока не достигнет её. При этом на переднем фронте зоны сжатия жидкость как бы слегка «проминается», и всё это выглядит как перетекание освобождающейся энергии деформации с заднего фронта зоны сжатия в сжимаемую жидкость на её переднем фронте. Таким образом, картина несколько отличается от «классики» — возле заглушки мы имеем ещё невозмущённую несжатую неподвижную жидкость, к ней стремительно движется фронт сжатия, а от входа трубы с той же скоростью и в том же направлении уже движется фронт спада давления.
Когда передний фронт зоны сжатия достигает заглушки (этап 6), он как бы «упирается» в неё, поскольку впереди больше нет жидкости, которую можно было бы сжать. Теперь «разряжаемая» жидкость на заднем фронте области сжатия действительно начинает двигаться обратно ко входу в трубу, поскольку для освобождаемой энергии деформации остаётся только один вариант — превратиться в кинетическую энергию жидкости. Однако при этом надо разогнать и всю жидкость на участке от заднего фронта зоны сжатия до входа в трубу, что занимает некоторое время. Поэтому задний фронт давления несколько «размывается», как показано на этапе 7. Впрочем, по мере разгона жидкости в обратном направлении эта «размытость» заднего фронта становится всё менее выраженной и, в конце концов, картина приближается к «классической» фазе (6). Этот механизм преобразует относительно мощный, но короткий импульс первичного удара в более слабый, но имеющий «стандартную» (т.е. ту же, что при заполнении пустой трубы) длительность — такую же, как и во всех последующих циклах.
Наконец, развитие процесса полностью переходит в «классические» рамки: зона сжатия сокращается (этап 7) и в последнюю очередь исчезает возле заглушки — этап 8, «классическая» фаза (6). Затем наступает фаза разрежения, которая при достаточной силе гидроудара сопровождается отрывом жидкости от заглушки — этап 9, «классическая» фаза (7). Однако за счёт «размывания» заднего фронта и необходимости разгона при обратном ходе всей жидкости в трубе скорость при этом будет меньше исходной скорости потока, даже в идеальном случае — когда нет необратимых потерь.
Остаётся выяснить вопрос, насколько изменится сила гидроудара по сравнению с пустой трубой? Здесь картина более сложная, чем в рассмотренной чуть выше горизонтальной трубе. Пока зона сжатия расширяется и её передний фронт не достиг заглушки, за счёт «проминания» невозмущённой жидкости, сжимаемость которой равна сжимаемости останавливаемой жидкости, скачок давления будет в корень из двух раз меньше, чем при гидроударе непосредственно в заглушку (кинетическая энергия преобразуется в деформацию, распространяющуюся в обе стороны от места начального столкновения). Однако если изначально неподвижной жидкости в трубе меньше, чем вновь прибывшей, то, когда передний фронт зоны сжатия достигает заглушки, сила гидроудара (скачок давления) там достигает тех же значений, что и в случае пустой трубы.
А вот длительность первого сжатия в любом случае будет меньше и на участке от места возникновения гидроудара до заглушки равна
где tC1 — длительность стадии сжатия первого цикла гидроудара; l — расстояние от места возникновения гидроудара до входа в трубу; с — скорость распространения ударной волны в трубе, рассчитываемая по формуле (5).
Длительность первого сжатия на участке от входа в трубу до места возникновения гидроудара будет такой же, как и при заполнении пустой трубы и должна рассчитываться по формуле (9).
Для всех последующих циклов гидроудара длительности стадий сжатия и разрежения определяются уже полной длиной трубы от входа до заглушки и не отличаются от заполнения пустой трубы. Поэтому они должны рассчитываться по тем же формулам (6)—(10). Однако энергия гидроудара по сравнению с пустой трубой уменьшается в число раз, равное соотношению длительностей первой стадии сжатия
kE = tC1 / tCЗ = (2 · l / c) / (2 · L / c) = l / L (22),
где kE — отношение энергии гидроудара в частично заполненной трубе к той же энергии при заполнении пустой трубы; tC1 — длительность стадии сжатия первого цикла гидроудара в частично заполненной трубе, рассчитываемая по формуле (21); tCЗ — длительность стадии сжатия у заглушки при гидроударе в пустой трубе, рассчитываемая по формуле (6); l — расстояние от места возникновения гидроудара до входа в трубу; L — полная длина от заглушки до входа; с — скорость распространения ударной волны в трубе.
Соответственно, скорости жидкости и скачок давления при всех последующих стадиях гидроудара в частично заполненной трубе будут отличаться от случая пустой трубы в √kE раз (квадратный корень из соотношения энергий). С учётом того, что кинетическая энергия здесь прямо пропорциональна массе жидкости, а в масса жидкости в трубе с неизменным сечением — её длине, это соотношение определяется квадратным корнем из отношения длины незаполненной части трубы к полной её длине √(l / L).
Мы рассмотрели столкновение потока с неподвижной жидкостью. Однако жидкость, в которую ударяет поток, может и сама двигаться в ту или иную сторону. Но здесь мы уже имеем дело со столкновением потоков.
Гидроудар в результате столкновения потоков
Гидроудар может возникнуть не только при столкновении потока c неподвижной жёсткой заглушкой или задвижкой, но и в случае его столкновения с другим потоком, движущимся по той же трубе. При этом один поток может «догнать» другой, движущийся в том же направлении, либо испытать «лобовое столкновение» с потоком, движущимся навстречу.
Эта ситуация отнюдь не редкая. Она может возникнуть практически в любом закольцованном трубопроводе, например, в домовой жидкостной отопительной системе в момент её заполнения теплоносителем, если слесари неправильно откроют вентили.
Тем не менее, расчёт здесь очень прост — в случае встречного столкновения повышение давления (т.е. сила гидроудара) равно сумме повышений давлений для каждого из потоков, если бы он столкнулся с неподвижной преградой. В случае же попутного удара более быстрого потока в «хвост» более медленного повышение давления будет равно разности скачков давлений гидроударов каждого из потоков о неподвижную преграду. Это следует из формулы Жуковского, где повышение давления прямо пропорционально изменению скорости двигавшегося потока.
Дальнейшее развитие событий протекает аналогично гидроудару в частично заполненной вертикальной трубе за одним исключением — поскольку в этой трубе нет жёстких заглушек, жидкость может не остановиться, а продолжить движение в том направлении, в котором двигался более «сильный» поток, т.е. поток с большей энергией или подпитываемый внешним источником (конечно, скорость потока при этом изменится).
Гидроудар с утечками (неполный гидроудар)
Ещё один вариант «из жизни» — это наличие утечек из трубы во время гидроудара. Причиной таких утечек может быть неполное перекрытие трубы заслонкой или заглушкой. Другая распространённая причина — наличие в трубе помимо входа, через который вливается поток, дополнительных отверстий (созданных специально или аварийных — в данном случае не так важно). Суммарная площадь таких отверстий или незакрытого просвета, естественно, должна быть меньше внутреннего сечения трубы, иначе гидроудара не будет в принципе, потому что не получится необходимого ограничения вытекающего из трубы потока.
Поскольку из-за наличия утечек жидкость не остановится полностью, то скачок давления будет меньше, чем при их отсутствии. Поэтому такой гидроудар иногда называют «неполным» в отличии от гидравлического удара с полной остановкой потока.
Гидроудар с боковой утечкой
Рассмотрим погружённую на некоторую глубину в стоячий водоём горизонтальную трубу неизменного сечения с заглушкой на одном конце, изначально пустую, в которой внезапно открывается вход и относительно небольшое отверстие сбоку недалеко от заглушки, причём сечение бокового отверстия существенно меньше внутреннего сечения трубы.
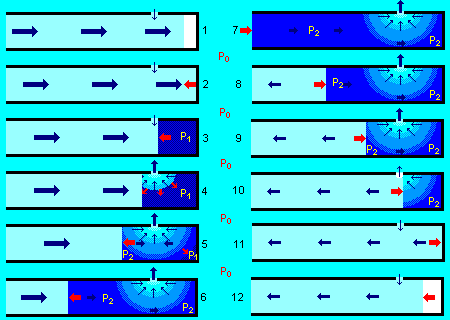 Схема развития гидравлического удара в трубе с боковой утечкой.
Голубым цветом обозначена внешняя среда с исходным давлением, белым — область пустоты, светло-голубым — область пониженного давления, синим — область повышенного давления (зона гидроудара). Синие стрелки показывают перемещение вещества среды (жидкости), красные — перемещение границы зоны повышенного давления (без существенного перемещения вещества). Цифрами обозначены стадии протекания процесса.
Сначала всё идёт, как и в фазе (1) «классического» гидроудара. Правда, если боковое отверстие уже открыто, через него также вливается дополнительный поток в пустую часть трубы, поэтому повышающийся уровень несколько тормозит основной поток, как и в случае горизонтальной трубы, предварительно частично заполненной жидкостью. Однако если боковое отверстие невелико, а основная труба не очень длинная, то такой жидкости поступит мало, и её влиянием можно пренебречь. Когда фронт основного потока пройдёт мимо отверстия, поступление жидкости сбоку сократится, но не прекратится (стадия 1). Это связано с тем, что давление движущегося потока меньше, чем давление неподвижной жидкости снаружи, поэтому через боковое отверстие будет продолжаться эжекционный подсос. Однако интенсивность его из-за меньшей разности давлений обычно существенно меньше, чем при заполнении пустой трубы, поэтому его влиянием на заполнение остатка трубы основным потоком в подавляющем большинстве случаев также можно смело пренебречь.
Затем поток достигает заглушки (стадия 2), останавливается, начинается его сжатие и формируется ударная волна, движущаяся ко входу в трубу (стадия 3). При этом давление возле заглушки в соответствии с формулой Жуковского достигает максимального давления P1. Если на стадиях 1–3 боковое отверстие закрыто клапаном и внутрь трубы через него ничего не поступает, процесс вообще ничем не будет отличаться от фаз (1)–(3) «классического» гидроудара.
Отличия начинаются, как только ударная волна и зона резко возросшего давления достигают бокового отверстия (стадии 3 и 4). Тут же часть жидкости под воздействием этого давления начинает выбрасываться наружу со скоростью v1. При этом возле отверстия возникает зона быстрого движения жидкости и вызванное этим пониженное (относительно гидроудара) давление. Граница такой зоны начинает распространяться в стороны от отверстия. Однако, по мере удаления от отверстия скорость устремляюшегося туда потока резко убывает (вблизи — обратно пропорционально квадрату расстояния, подальше из-за ограничений внутреннего пространства трубы — менее резко). Поэтому вокруг отверстия до фронта падения давления создаётся градиент давления — чем дальше от отверстия, тем выше давление. Наряду с распространением от отверстия зоны понижающегося давления, основная ударная волна продолжает движение в сторону входа в трубу, расширяя зону сжатой жидкости. Оба эти процесса происходят со скоростью распространения упругих деформаций, близкой к скорости звука (ещё раз подчеркну, что не следует путать высокие скорости фронтов давления с относительно низкими скоростями перемещения самой жидкости — в силу низкой сжимаемости жидкостей в заполненном сосуде её малейшие перемещения способны вызвать огромные перепады давления).
Но жидкость на участке от входа в трубу до бокового отверстия не остановилась полностью — она продолжает двигаться, вытекая в боковое отверстие. И хотя эта остаточная скорость движения v2 теперь значительно уменьшилась по сравнению с скоростью заполнения пустой трубы v0, она есть. Поэтому между входом и отверстием жидкость не останавливается полностью, а лишь тормозится. Впрочем, и этой разности скоростей при малом сечении бокового отверстия вполне достаточно для повышения давления до величины P2, весьма немалой, но, конечно, меньше силы гидроудара полностью остановленной жидкости P1. Это имеет место на стадиях 5 и 6.
Однако если со стороны входа жидкость, выходящая в отверстие, компенсируется вновь прибывающими порциями, то у заглушки дела обстоят иначе, — ведь жидкость уходит в отверстие со всех сторон, а новой возле заглушки взяться неоткуда. Не образуется ли там разрежение? Нет, не образуется! Конечно, по мере распространения фронта падения давления от отверстия давление там снизится с уровня P1, и, как только оно станет ниже уровня P2, жидкость со стороны входа начнёт перетекать к заглушке, поддерживая там давление, близкое к P2. Это обусловлено тем, что у стенки трубы, противоположной боковому отверстию, скорость движения жидкости в отверстие весьма мала, и падение давления по сравнению с P2 там незначительно. Поэтому, как только за счёт утекающей наружу жидкости давление у заглушки станет меньше его величины, под действием разности давлений возникнет компенсирующее течение, показанное на рисунке горизонтальной тёмно-синей стрелкой под отверстием. Конечно, по закону Бернулли это движение также несколько уменьшит давление, поэтому, строго говоря, давление у заглушки будет меньше P2. Но если утечка достаточно мала, скорость компенсирующего течения будет невысокой, и тогда можно считать, что давление у заглушки практически равно P2.
Кроме того, пока возле заглушки сохраняется область исходного максимального давления P1, жидкость в отверстие со стороны заглушки устремляется за счёт этого давления, а не за счёт её перетекания от входа по противоположной от отверстия стенке трубы. Поэтому в это время остаточный поток со стороны входа равен половине утечки через отверстие (стадия 5). И лишь после того, как область начального — самого высокого — давления P1 у заглушки исчезнет, вся утечка будет происходить за счёт остаточного потока от входа в трубу (стадия 6), при этом его скорость возрастёт вдвое по сравнению с предыдущей стадией, а давление P2 соответственно понизится.
Особо подчеркну, что область снижения давления у отверстия утечки не распространяется на всю трубу — ни ко входу, ни к заглушке! Давление относительно P2 начинает снижаться лишь непосредственно возле этого отверстия на расстояниях, меньших внутреннего диаметра трубы.
Наконец, ударная волна достигает входа в трубу и начинается обратное движение (стадия 7). В этот момент давление во всей трубе за исключением блиайших окрестностей отверстия равно P2 (на участке между отверстием и заглушкой — чуть меньше).
Теперь от входа начинает увеличиваться область давления, близкого к давлению вне трубы. В ней жидкость движется ко входу со скоростью, обусловленной давлением P2 и по величине равной v0 – 2 · v2 (если не учитывать необратимые потери). Это стадия 8. В оставшейся области высокого давления жидкость по-прежнему продолжает двигаться к отверстию с остаточной скоростью v2.
Когда волна спада давления доходит до области пониженного давления возле отверстия (стадия 9), она как бы «срезает» её, практически не влияя на истечение жидкости из отверстия до тех пор, пока не пройдёт через отверстие. Как только это произойдёт, истечение жидкости прекращается (быстро, но не мгновенно, поскольку жидкость вытекала со значительной скоростью и имеет заметную инерцию). При большой скорости истечения через отверстие в силу инерции потока, возможен даже его отрыв от основной массы жидкости в трубе и образование небольшой области пустоты (стадия 10). Если же отрыва не произошло, то после остановки потока через отверстие начинается эжекционный подсос, как и на стадии 2.
Когда высокого давления в трубе не останется, вся жидкость в трубе будет двигаться в направлении от заглушки обратно ко входу в трубу (стадия 11). К этому времени пустота, образовавшаяся в месте отрыва потока утечки, скорее всего, уже «схлопнется», породив небольшой гидроудар. Однако в силу своей относительно малой энергии он не оказывает заметного влияния на жидкость в трубе и быстро затухает. По окончании процессов этого «дочернего» гидроудара через отверстие утечки опять-таки начинается эжекционный подсос.
Если гидроудар был сильным, то жидкость отрывается от заглушки и в этой области образуется пустота (стадия 12). Однако критерием отрыва в данном случае является не давление полной остановки потока P1, а давление возле заглушки в конце этапа сжатия, несколько меньшее, чем P2. Оторвавшаяся жидкость под действием внешнего давления у входа в трубу постепенно останавливается, а затем вновь устремляется в трубу, повторяя стадию 1. Если пустая область распространилась до отверстия утечки, относительно небольшой эжекционный подсос через него сменяется прямым заполнением трубы, ослабляющим силу последующих циклов гидроудара и способствующим их быстрейшему затуханию.
Мы рассмотрели лишь наиболее существенные моменты, однако уже понятно, что гидроудар с утечками — процесс гораздо более сложный, чем «классический» гидроудар без утечек. При более внимательном анализе выявляется ещё множество нюансов, дополнительно усложняющих картину. Но их влияние обычно весьма незначительно и потому они заслуживают внимания лишь в отдельных, особо экзотических случаях.
Гидроудар с торцевой утечкой
Если отверстие утечки находится в торце трубы, то и сам процесс, и его расчёт существенно упрощаются.
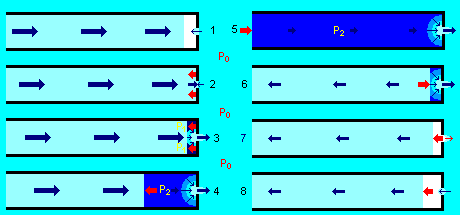 Схема развития гидравлического удара в трубе с торцевой утечкой.
Голубым цветом обозначена внешняя среда с исходным давлением, белым — область пустоты, светло-голубым — область пониженного давления, синим — область повышенного давления (зона гидроудара). Синие стрелки показывают перемещение вещества среды (жидкости), красные — перемещение границы зоны повышенного давления (без существенного перемещения вещества). Цифрами обозначены стадии протекания процесса.
На стадии 1 первичное заполнение трубы происходит с двух сторон — основным потоком через вход трубы и небольшим (в силу меньшего сечения) потоком через отверстие в торце-заглушке. Как и в случае боковой утечки, уровень жидкости, повышающийся возле заглушки за счёт дополнительного потока, несколько затормозит основной поток, — ведь основной поток будет заполнять горизонтальную трубу, уже частично заполненную жидкостью. Однако если это отверстие невелико, а сама труба не очень длинная, то такой жидкости поступит мало, и её влиянием можно пренебречь. Если же за заглушкой жидкости нет либо отверстие закрыто клапаном, эта стадия вообще ничем не отличается от фазы (1) «классического» гидроудара.
Но как только поток достигает заглушки, сразу же начинаются отличия. Часть потока, оказавшаяся напротив отверстия, сразу «влетает» туда, мгновенно останавливая втекавшую жидкость (если таковая была) — тут происходит встречный гидроудар. Остальная часть потока резко тормозится об заглушку и давление в соответствии с формулой Жуковского тут же достигает максимального давления P1, обусловленного полной скоростью потока перед остановкой v0 (стадия 2). Под действием этого давления жидкость вокруг отверстия утечки устремляется туда со всех сторон, создавая разрастающуюся область быстрого движения с пониженным относительно P1 давлением. В то же время основная ударная волна начинает своё движение ко входу в трубу. Это соответствует стадии 3.
Как и в случае боковой утечки, по мере удаления от отверстия скорость устремляюшегося туда потока убывает обратно пропорционально квадрату расстояния. Поэтому от отверстия и до фронта падения давления создаётся градиент давления — чем дальше от отверстия, тем выше давление. Однако, когда диаметр этой области становится равным внутреннему диаметру трубы, стенки трубы ограничивают её, и при дальнейшем распространении ударной волны по трубе в остальной части трубы давление уже одинаково. И, конечно, жидкость в трубе не останавливается полностью, а продолжает двигаться с небольшой скоростью v2, компенсирующей поток, уходящий наружу через отверстие утечки со скоростью v1. Поэтому на стадии 4 давление будет равно величине P2, которая меньше максимального давления при полной остановке P1.
Затем ударная волна достигает входа трубы и начинает обратное движение (стадия 5). В отличии от боковой утечки, зон, где жидкость неподвижна или движется в обратную сторону, в этот момент нет. Во всей трубе жидкость движется к заглушке (точнее, к отверстию в ней) со скоростью v2 и давление равно величине P2. Единственное исключение составляет область в непосредственной близости от отверстия утечки, где давление снижается из-за ускорения жидкости, направляющейся наружу.
По мере обратного движения ударной волны и сокращения области высокого давления, жидкость в области высокого давления продолжает двигаться к отверстию в заглушке, а жидкость в части трубы, где давление уже упало, начинает двигаться ко входу в трубу со скоростью, обусловленной давлением P2 и по величине равной v0 – 2 · v2 (если не учитывать необратимые потери). Когда волна спада давления доходит до области пониженного давления возле отверстия (стадия 6), она как бы «срезает» её, практически не влияя на истечение жидкости из отверстия до тех пор, пока не дойдёт до торцевой заглушки.
В момент, когда давление во всей трубе упало, вся жидкость в ней движется обратно ко входу, а то, что успело «выскочить» в отверстие утечки — в противоположную сторону. Поэтому при достаточной силе гидроудара оба потока отрываются от стенок трубы и друг от друга, и возникает пустота. Следует особо подчеркнуть, что, в отличие от боковой утечки, когда отрывы потока утечки от отверстия и основного объёма жидкости от торца заглушки происходят в разных местах и в разное время, из-за чего могут образоваться две области пустоты с различным временем жизни, в случае торцевой утечки всегда образуется единая область пустоты в одном месте и в одно время (стадия 7).
Но поток утечки слабее основного потока в трубе, и потому (если не предприняты специальные меры) его область отрыва быстро заполняется жидкостью снаружи, которая затем начинает поступать внутрь трубы (стадия 8). Это может произойти задолго до того, как основная масса жидкости в трубе после постепенного торможения снова начнёт движение к заглушке, повторяя стадию 1. Впрочем, не следует забывать, что «долго» в данном случае обычно измеряется милли-, а то и микросекундами!
Таким образом, в отличие от боковой утечки, при гидроударе с торцевой утечкой не происходит перетекания жидкости мимо отверстия утечки, и давление во всей трубе на протяжении всего этапа сжатия одинаково и равно P2. Остаточная скорость жидкости также одинакова по направлению и величине (кроме небольшой области возле самой заглушки). Пустота тоже возникает только один раз и в одном месте. Это существенно упрощает расчёты, особенно в том случае, когда отверстие утечки достаточно велико и остаточная скорость v2 относительно высока.
Расчёт гидроудара с утечкой
Важнейшим параметром для расчёта является остаточная скорость v2. В силу уравнения непрерывности она соотносится со скоростью истечения жидкости из дополнительного отверстия v1 как
где v2 — остаточная скорость течения жидкости в трубе на участке от входа до отверстия утечки; v1 — скорость истечения из отверстия утечки; S1 — площадь сечения отверстия утечки; S — площадь внутреннего сечения трубы.
В то время, когда давление у заглушки ещё остаётся первоначально высоким (стадия 5 при боковой утечке), скорость остаточного потока следует считать вдвое меньшей, поскольку со стороны заглушки жидкость к отверстию поступает самостоятельно, а остаточный поток от входа обеспечивает лишь «свою» половину утечки:
v2 = v1 · S1 / (2 · S) (24).
Но если утечка происходит через торцевую заглушку или в непосредственной близости от неё, время действия этой формулы весьма мало, и тогда при расчётах вполне достаточно формулы (23).
Таким образом, всё сводится к определению скорости утечки жидкости через отверстие v1. Если считать, что среда вне трубы не оказывает существенного сопротивления истечению жидкости, то скорость рассчитывается аналогично формуле (12):
где v1 — скорость утечки; √ — операция извлечения квадратного корня; ρ — удельная плотность жидкости; ΔP — разность давлений внутри и снаружи трубы.
Это наибольшая возможная скорость утечки, когда за отверстием находится не жидкость, а воздух или вакуум. При этом в начальный момент ΔP не может превышать P1. По мере того, как давление возле отверстия падает, уменьшается и скорость. В свою очередь, падение скорости приводит к некоторому повышению давления. Это выглядит как затухающий колебательный процесс и при расчёте численными методами также проявится и на бумаге. На самом деле подробности этого процесса малоинтересны — в любом случае весь он не превышает времени, необходимого ударной волне для того, чтобы пересечь внутренний диаметр трубы, — т.е. считанные микросекунды. Гораздо важнее установившееся значение скорости утечки во время всей оставшейся длительности этапа сжатия. Но эта скорость зависит от давления P2, а давление, наоборот, от неё. Получается замкнутый круг, однако численными методами с помощью последовательного приближения решение найти достаточно легко — как уже говорилось, данные расчёта образуют сходящийся ряд значений. Для грубой оценки или при существенной разности сечений трубы и бокового отверстия будет достаточно формулы (25). Для точного расчёта необходимо учесть все условия утечки, в том числе длину и другие параметры канала, по которому утекает жидкость. Кроме того, надо учесть и потери давления, возникающие при сужении канала протекания жидкости — переход от большого внутреннего сечения основной трубы, где возникает гидроудар, к малому проходному сечению отверстия утечки. Такой режим расчёта поддерживает программа SiP.
Гидроудар с большими утечками
Если утечка достаточно велика, то характер гидроудара меняется кардинальным образом. По мере увеличения отверстия утечки при прочих равных условиях остаточная скорость v2 увеличивается, поэтому если сначала энергии, запасённой в упругой деформации, хватало на отрыв жидкости от заглушки, то затем её для этого уже недостаточно, а при дальнейшем увеличении отверстия этой энергии уже может не хватить даже для снижения давления возле заглушки ниже давления у входа в трубу. В результате при гидроударе с большой утечкой отсутствует этап разрежения, как он понимается в «классическом» гидроударе (давление не падает ниже внешнего давления у входа в трубу, не говоря уже об отбое с отрывом жидкости от заглушки), а значит, в принципе не возможны повторные циклы, связанные с обратным движением жидкости. Точнее, затухающие колебания давления по-прежнему имеют место, однако давление всё время остаётся достаточно высоким, а жидкость уже не меняет направления своего движения, лишь несколько меняя скорость, которая в конце концов стремится к скорости стационарного потока в канале переменного сечения, определяемой давлениями снаружи трубы — у её входа и у отверстия утечки.
Что можно выбрать критерием большой утечки при гидроударе? Представляется логичным считать утечку большой, когда остаточная скорость v2 достигает половины от исходной скорости потока v0 или превышает её:
Тогда в момент окончания этапа сжатия и падения давления накопленной энергии деформации уже недостаточно для создания обратного движения жидкости — она лишь замедляет своё движение в прежнем направлении, но никогда не движется вспять!
При этом без расчёта нельзя сказать, будет ли выполняться этот критерий при данном соотношении внутреннего сечения трубы и отверстия утечки — это зависит не только от соотношения сечений, но и от других факторов, прежде всего от скорости потока (чем меньше разность сечений и чем меньше скорость, тем больше вероятность признания утечки «большой»), а также от того, что находится за отверстием утечки: пространство, заполненное атмосферным воздухом или вакуум, либо не ограниченная стенками жидкость при том или ином давлении, либо узкая труба — пустая или чем-то заполненная... Впрочем, соотношение сечений основной трубы и отверстия утечки 400:1 и более (т.е. не менее двадцатикратной разности диаметров) обычно даёт «большую» утечку лишь при столь малых скоростях исходного потока, что говорить о гидроударе в этих случаях можно только теоретически — он слишком слаб. На практике и десятикратной разности диаметров (соотношение сечений 100:1) очень часто вполне хватает для того, чтобы считать утечку достаточно малой.
О сверхъединичности гидроударов
Выше мы рассматривали гидроудар с «традиционных» механистических позиций. В то же время есть довольно много сведений, что при сильных одиночных гидравлических ударах или при множественных относительных слабых (в том числе при кавитации) имеют место необычные явления, не сводимые к механике и, возможно, приводящие к появлению некоей дополнительной энергии. Особенно часто отмечают видимое глазом свечение и аномальный нагрев микрообъёмов жидкости в зоне кавитации. Реже обращают внимание на весьма необычные с «механической» точки зрения результаты кавитационной коррозии, заключающиеся не только в традиционном разрушении и изъязвлении материалов, но и образовании различных «наплывов» и выступов (часто это объясняют «эффектом ковки», который оказывают кавитационные пузырьки на металл деталей, однако здесь имеет место явный перенос потоком жидкости материала корродировавшей детали, поскольку расстояние между зонами разрушения и осаждения материала в таких случаях часто на порядки превышает размеры «молотов»-пузырьков).
Следует отметить, что на короткое время гидроудар ставит вещество в крайне экстремальные условия — давление может возрастать на сотни и даже тысячи атмосфер, что соответствует условиям на глубине в десятки километров, где вещества приобретают экзотические свойства и претерпевают необычные трансформации (например, твёрдые вещества проявляют текучесть, а графит может превратиться в алмаз). Но даже если давление вырастает не очень сильно (на десятки атмосфер, а то и просто на несколько атмосфер), скорость изменения давления для каждой попавшей под удар частички вещества очень высока — 1012 Па/с и более (не путать со скоростью распространения ударной волны!). Она вполне сравнима, а то и превосходит скорости изменения давления при взрывах. При этом образующаяся во время взрывов газовая или плазменная среда является весьма сжимаемой, — она «амортизирует» удар, и чуть дальше от эпицентра давление нарастает гораздо более плавно. Но во время гидроудара из-за малой сжимаемости жидкостей и высокой жёсткости материала стенок этот сверхрезкий скачок давления воздействует практически на весь объём, участвующий в гидроударе. Столь резким скачкам давления соответствуют и гигантские ускорения и торможения частичек вещества при прохождении через них фронта ударной волны. Правда, длятся они нано- и пикосекунды, поэтому общее смещение частиц жидкости мало и обычно составляет, в соответствии с её малой сжимаемостью, микрометры или нанометры. Тем не менее, по меркам атомов и молекул, эти сдвиги весьма велики, и возникающие при этом силы тоже немаленькие. Так что нельзя исключить, что такие «наносдвиги» могут стать причиной каких-то необычных явлений.
Тем не менее, на данной странице такие явления не рассматривается, поскольку если что-то подобное и имеет место, то его воздействие весьма мало и не оказывает никакого заметного влияния ни на одиночные гидроудары (в трубопроводах), ни на множественные повторяющиеся гидроудары в гидравлических таранах (там они происходят в условиях проточного движения рабочего тела и с относительно большим периодом, обычно раз в несколько секунд). Гидроудары исследовались многими людьми в течении многих лет, и явные аномалии давно были бы замечены. Не влияют подобные явления и на расчёт параметров единичного рабочего цикла в случае частых повторных гидроударов. Однако в условиях частого (десятки и сотни раз в секунду) повторения в замкнутом объёме циркулирующего рабочего тела результаты таких эффектов могут суммироваться и проявляться вполне ощутимо. В таком случае, резонно с их помощью попытаться объяснить работу некоторых конструкций Виктора Шаубергера и, возможно, Ричарда Клема, — а тогда эти явления требуют подробного и тщательного изучения.
♦
|