Конструкции с дисбалансом
Проекты с дисбалансом сторон колеса появились практически в то же время, что и конструкции со свободным и принудительным перемещением грузов. Дальнейшим развитием этой идеи стали попытки использовать цепи с различной длиной нисходящей и восходящей ветвей (а следовательно, с различным их весом) или с различными интервалами между грузами на этих ветвях, а также попытки создать цепи поплавков, у которых одна ветвь находится в воде или другой среде с высокой плотностью, а другая — в среде с низкой плотностью, например, в воздухе.
Следует особо подчеркнуть, что в данном случае под «дисбалансом» имеется в виду именно разность весов нисходящей и восходящей ветвей цепи или сторон колеса. Не следует путать этот дисбаланс с дебалансом — несимметричностью вращающихся деталей, созданной не с целью получения разницы в весе с разных сторон от оси, а для обеспечения колебательного движения тех или иных частей конструкции, как это имеет место, например, в интересных установках Э.И.Линевича.
Колесо д'Оннекура
Цепи с разной длиной ветвей
Цепи с разной плотностью ветвей
Установка «AvalancheDrive»
Упрощённый вариант
Причины неработоспособности «лавинного двигателя»
Гидравлический ленточный двигатель
Цепи поплавков в разных средах
«Полусухая» цепь поплавков
Водо-масляная цепь поплавков
Колесо д'Оннекура
Именно к этому типу относится первый известный европейский проект «вечного двигателя» Вийяра д'Оннекура, датируемый 1235 годом. В этом устройстве предлагалось подвесить к ободу колеса 7 молотов, каждый из которых, по сути, представлял собой груз на небольшом рычаге. Автор особо подчёркивал необходимость нечётного числа элементов. Кинематическая схема этого устройства показана на рисунке.
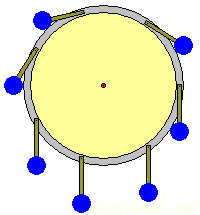 Кинематическая схема колеса д'Оннекура.
Как ни странно, это колесо вполне могло вращаться! Почему? Обратите внимание на два верхних элемента. Очевидно, что в какую бы сторону не вращалось колесо, «естественным» путём — под действием одной лишь силы тяжести — такое положение они принять не могут. Для этого необходимо приложить хотя бы к одному из них внешнее воздействие, скажем, в нужный момент перекинуть рычаг с грузом вручную. Вот эта дополнительная внешняя работа и позволит колесу вращаться! Естественно, полезной работы с такого колеса удастся получить не больше, чем было затрачено внешней дополнительной работы. Кстати, подвеска грузов на рычагах нужна в этой конструкции именно для того, чтобы обеспечить возможность их перемещения с помощью дополнительной внешней силы.
Если же отказаться от дополнительного перемещения грузов с помощью внешней силы, то нет никакой разницы, висят ли грузы на неподвижных рычагах или жёстко закреплены на ободе колеса. При этом возможны два распределения грузов — симметричное (уравновешенное) и несимметричное (неуравновешенное).
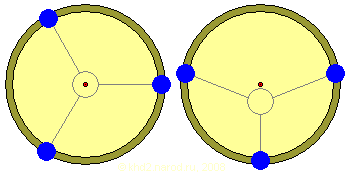 Симметричное уравновешенное (слева) и несимметричное неуравновешенное (справа) распределение грузов на ободе колеса. Серым цветом показано положение центров масс систем грузов.
Очевидно, что оба они не приводят к самостоятельному вращению колеса. В случае уравновешенного распределения грузов, хотя число грузов слева и справа от оси может быть различным, в силу законов геометрии их плечи всегда соотносятся таким образом, что суммарные вращающие моменты с обеих сторон взаимно компенсируют друг друга (именно на этом основана обычная балансировка автомобильных колёс). При неуравновешенном расположении грузов колесо также не будет вращаться — оно покачается влево-вправо и из-за трения в конечном счёте остановится в соответствии с самым нижним положением центра масс всей системы грузов — то есть это эквивалентно размещению в этом месте обода одного груза, вес которого соответствует сумме весов грузов в верхней и нижней половинах, умноженных на синус угла между направлением от груза к оси колеса и горизонталью (с учётом знака синуса). И, конечно, в обоих случаях не имеет значения, является ли общее число грузов чётным или нечётным!
Кстати, колёса с дисбалансом требуют минимума затрат для экспериментальной проверки — если в доме есть велосипед, его переднее колесо к Вашим услугам, а грузики к ободу можно примотать скотчем...
Цепи с разной длиной ветвей
Это тип конструкций исходит из простой мысли: если сделать длину одной ветви вертикальной замкнутой цепи с грузами больше другой — например, оттянуть её в сторону дополнительным шкивом, то число грузов там, а, следовательно, и масса этой ветви, будет больше, чем у более короткой, поэтому должен возникнуть дисбаланс и цепь начнёт вращаться сама по себе! Чуть подумав, можно прийти к выводу, что не обязательно делать десятки и сотни грузов и скреплять их между собой, — однородный тяжёлый, но гибкий ремень или обычная металлическая цепь будут иметь ту же самую кинематику, что и множество мелких грузиков с минимальным расстоянием между ними, но гораздо проще и технологичнее в изготовлении.
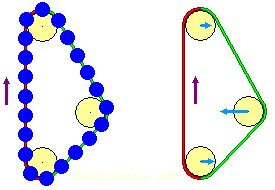 Замкнутые цепь с грузами (слева) и однородный ремень (справа) с ветвями разной массы. Зелёным выделена «ускоряющая» более тяжёлая ветвь, а красным — лёгкая «тормозящая», светло-синими стрелками показаны горизонтальные силы на осях шкивов.
Действительно, взглянув на рисунки (особенно левый, с отдельными грузами), можно подумать: «а ведь и правда, кажется, что это должно работать!» Однако в реальной жизни такая конструкция и не подумает крутиться. Почему? Да потому, что «лишний» вес более тяжёлой ветви компенсируется горизонтальными усилиями в осях шкивов. В самом деле, давайте ослабим натяжение так, чтобы ремень сильно провис. Разность масс левой и правой ветвей стала ещё больше, а вот ощущение, что всё это будет крутиться само по себе, практически исчезло! Это неудивительно, поскольку теперь эта «горизонтальная» составляющая стала очевидной.
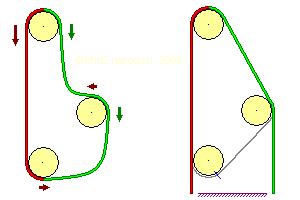 Слева — ослабленный ремень с разной массой ветвей. Красными показаны «тормозящие», а зелёными — «ускоряющие» силы. Справа — условие разрезания ремня, при котором он не соскользнёт со шкивов (синей риской показано место разреза).
Дело в том, что «тянуще-тормозящая» (вертикальная) сила равна весу того или иного фрагмента ремня, умноженному на косинус его отклонения от вертикали. А вес, умноженный на синус этого угла, даёт «нейтральную» горизонтальную силу, действующую на оси шкивов. Чем большую разность ветвей мы хотим создать, тем больший наклон к вертикали мы вынуждены использовать, и, соответственно, с единицы длины такой ветви уменьшается «полезная» вертикальная составляющая и увеличивается «нейтральная» горизонтальная, поэтому очевидная разность в весе ветвей ремня не вызывает его вращения. Если выполнить тщательный расчёт, то окажется, что сумма тормозящих сил в точности равна сумме ускоряющих, поэтому никакого самопроизвольного движения не будет, как и в случае колеса с симметричным расположением грузов на ободе. Если же масса какой-то части ремня или цепи будет принудительно увеличена за счёт дополнительного груза, то всё закончится тем, что утяжелённый фрагмент устремится в самое нижнее положение и там в конце концов остановится — аналогично колесу с несимметричным расположением грузов.
Но ведь несложно убедиться на опыте, что если разрезать эту цепь (ремень) в любом месте, то она соскользнёт в ту или иную сторону?! Безусловно, кроме одной точки разреза — той, что обеспечит равную высоту свободно повисших разрезанных концов. Однако и в этом случае всё будет находиться в состоянии неустойчивого равновесия, а если трение в шкивах мало, то это равновесие нарушит малейшее воздействие на цепь, и она немедленно соскользнёт вниз! Но когда кольцо цепи не разрезано, любое усилие в её верхней части вызывает аналогичное компенсирующее усилие внизу и наоборот, поэтому никакого «желания» куда-либо перемещаться у неё не может возникнуть в принципе.
Здесь в наиболее чистом виде представлена идея, которую очень часто пытаются применить в менее очевидных вариантах, но всё дело в том, что при равномерном распределении веса на единицу длины вертикальное усилие всегда зависит только от разности верхнего и нижнего уровней, а не от траектории пути между ними — в полном соответствии с формулой для потенциальной энергии тела в гравитационном поле.
Цепи с разной плотностью ветвей
Изменяя длину ветвей однородной цепи, нам не удалось добиться дисбаланса, обеспечивающего устойчивое самовращение. Но можно изменить плотность грузов на разных ветвях цепи, сохранив их длину одинаковой. В этом случае разность весов ветвей будет несомненной, и эта разность будет направлена строго вертикально. Уж здесь-то, кажется, ничто не может помешать самовращению! К этому классу конструкций относится бразильский проект «АваланчДрайв».
Установка «AvalancheDrive»
Проект «АваланчДрайв» уже несколько лет продвигает бразильский изобретатель Мурило Лучиано (Murilo Luciano) из Сан-Пауло (по-английски Avalanche — лавина, Drive — здесь, как и в современной музыке, это фигуральное обозначение энергии и силы). Другое название этого проекта — «гравитационный лавинный двигатель». В нём предлагается использовать «складную» цепь с роликами-грузами. В нисходящей ветви звенья этой цепи сложены и грузы «упакованы» максимально плотно. В восходящей ветви цепь растянута и грузы находятся на довольно большом расстоянии друга от друга, поэтому плотность их размещения там намного меньше, чем в восходящей ветви. В результате имеем существенную разность веса ветвей цепи при их одинаковой длине и одинаковой вертикальности. Скопление грузов в нисходящей ветви ассоциируется с горной лавиной, накапливающей вес по мере продвижения и сметающей всё на своём пути, — отсюда и эффектное название «лавинный двигатель». Все знают, что горная лавина способна отбросить со своего пути далеко в сторону встретившиеся ей камни, деревья, машины и даже дома.
В этой конструкции разные расстояния между грузами в восходящей и нисходящей ветвях обеспечиваются довольно хитроумной системой соединяющих соседние элементы тяг и распорок с защёлками-крючками. В вертикальных частях установки необходимое направление движения роликов-грузов задаётся направляющими специального профиля. Подобное инженерное решение обеспечивает разное расстояние между грузами в нисходящей и восходящей ветвях и в то же время не требует организации кинематической связи между верхним и нижним шкивами установки (кроме той, что возникает сама по себе за счёт движения цепочки элементов с грузами). Дело в том, что здесь восходящая ветвь не подтягивается через верхний шкив, а выталкивается снизу весом нисходящей ветви за счёт жёстких распорок между грузами — также, как горная лавина, ударившись о встретившийся поперёк пути склон, «выплёскивается» на него. Однако очевидно, что изготовление этой конструкции будет весьма трудоёмким, и сделать её вне заводских условий достаточно проблематично.
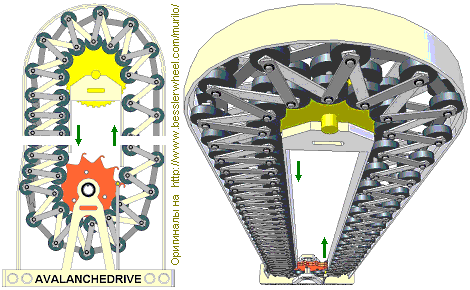 Иллюстрации к поздней версии проекта Мурило Лучиано (май 2009 г). В левой ветви видны сложенные распорки, обеспечиваюшие увеличенное расстояние между внешними грузами-роликами в правой ветви. Подробности этого варианта смотрите на сайте с авторским описанием проекта. Упрощённый вариант
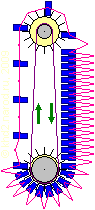
Упрощённый вариант.
|
Но обращаться на завод совсем не обязательно. Подобное устройство можно немного изменить, чтобы сделать более пригодным для самостоятельного изготовления. Такой упрощённый вариант показан на рисунке слева. Для этого потребуются:
-
· два одинаковых шкива (показаны светло-жёлтым) с прикреплёнными к ним пластинами-сепараторами грузов;
-
· две велосипедные звёздочки (показаны серым), жёстко соединённые со шкивами; соотношение звёздочек равно соотношению расстояний между грузами в восходящей и нисходящей ветвях;
-
· велосипедная цепь необходимой длины (показана фиолетовым, для получения большой длины можно срастить несколько цепей);
-
· а также комплект одинаковых грузов (показаны синим) в количестве, соответствующем размерам установки, соединённых между собой шарнирно скреплёнными жёсткими тягами (показаны ярко-розовым) либо просто верёвками.
Грузы могут иметь как прямоугольную форму (да хоть бы и кирпичи), так и круглую — с технической точки зрения и та, и другая обладают своими преимуществами и недостатками, но с точки зрения физики это не имеет значения. В нисходящей ветви грузы могут просто лежать друг на друге (как раз поэтому жёсткие тяги можно заменить верёвками), а в восходящей верхний груз поднимает все остальные с помощью соединяющих их тяг. Для предотвращения рассыпания и закручивания грузов и нисходящую, и восходящую ветви надо окружить направляющими, которые на рисунке не показаны. Соотношение расстояний между грузами, по большому счёту, определяется лишь соотношением звёздочек и размерами шкивов (на верхней половине верхнего шкива всегда должен быть хотя бы один груз), и теоретически может быть любым — хоть 1:2, хоть 1:20 (в последнем случае вес восходящей ветви составит лишь 5% от веса нисходящей)!
Кинематика движения грузов аналогична «Аваланчу», хотя механика работы несколько иная. Разный вес ветвей со всей очевидностью создаёт вращающий момент на нижнем шкиве. Через звёздочки с цепью это вращение передаётся верхнему шкиву, причём он вращается быстрее во столько же раз, во сколько расстояние между центрами масс грузов на восходящей ветви больше такого же расстояния на нисходящей. В результате верхний шкив своими пластинами-сепараторами подхватывает очередной груз, приблизившийся к нему по восходящей ветви, и быстро «перекидывает» его в стопку грузов нисходящей ветви, заодно подтаскивая к себе следующий восходящий груз с помощью соединяющих грузы тяг. При этом длина тяг может быть чуть больше расчётной — соотношение скоростей шкивов строго задаётся числом зубьев шестерён, и некоторая неравномерность интервалов между грузами в начале восходящей ветви непринципиальна, лишь бы грузы уверенно захватывались сепараторами верхнего шкива.
Итак, для российского варианта «лавинного двигателя» не требуются прецизионные токарные и фрезерные работы, а достаточно старого велосипеда (колёса, к ободьям которых надо прикрепить пластины-сепараторы, будут шкивами; как использовать цепь и звёздочки, уже сказано выше), а также потребуется некоторое количество кирпичей, верёвки, несколько труб или уголков для каркаса и направляющих и, конечно, руки, растущие «откуда надо».
Должен заметить, что к аналогичным решениям (правда, не на столь брутальном уровне, без кирпичей и велосипедов) пришли и другие люди, заинтересовавшиеся «лавинным двигателем» Мурило Лучиано, — например, Патрик Келли (Patrick Kelly).
Причины неработоспособности «лавинного двигателя»
Тем не менее не надо торопиться запасаться кирпичами и искать старые велосипеды. В упрощённом варианте явно виден момент, завуалированный в его бразильском аналоге — ускоренное вращение верхнего поднимающего шкива, в соответствии с законом рычага во столько же раз уменьшающее его усилия, направленные на подъём груза. Это сразу настораживает в ожидании подвоха. И действительно, простейший анализ показывает, что никакой прибавки энергии быть не должно, — вывод совершенно очевиден, если рассматривать полный цикл движения каждого груза в отдельности (ведь насколько груз опустится в нисходящей ветви, настолько же затем поднимется в восходящей).
Однако энтузиасты могут сказать — «двигатель потому и называется лавинным, что там работают не отдельные грузы, а их совокупность». Что ж, попробуем рассмотреть этот двигатель как совокупность грузов. В таком случае в качестве элементарного шага рабочего цикла удобно выбрать такое перемещение цепи грузов, когда следующий груз занимает место предыдущего. Очевидно, что это справедливо и для нисходящей, и для восходящей ветви, иначе в ходе работы в каком-либо одном месте постоянно нарастало бы скопление грузов, а в другом также постоянно нарастала бы их нехватка — вплоть до разрыва цепи, прекращающего работу установки. Итак, предположим, что расстояние между грузами в восходящей ветви равно h, их количество там равно n, а соотношение расстояний между грузами в восходящей и нисходящей ветвях равно k > 1. Тогда за один рабочий шаг в восходящей цепи n грузов поднимется на высоту h, а в нисходящей n · k грузов опустятся на высоту h / k. Посчитав работу каждой ветви как разность потенциальных энергий, мы увидим, что для нисходящей ветви коэффициенты k сократятся и формулы для обоих ветвей будут совершенно идентичными, то есть их работы одинаковы и энергетического выигрыша не наблюдается.
Обратите внимание — здесь не учитываются ни механизмы изменения плотности размещения грузов, ни характер привода восходящей ветви (выталкивание снизу, как в бразильском варианте, или подтягивание вверх, как в упрощённой конструкции) — они могут быть любыми и на результат не влияют.
И всё же можно возразить: «но ведь если всё стоит на месте, разница веса ветвей, то есть сил, и, соответственно, наличие крутящего момента очевидны?» Да, это так. Но — только пока всё стоит! Как только всё начнёт приходить в движение, силы тут же выровняются! Почему? Как известно, механическая сила рассчитывается как произведение массы тела на его ускорение. Массы всех элементов одинаковы, а вот ускорения... В соответствии с условием неразрывности цепи грузы на восходящей (обратной) ветви должны двигаться в k раз быстрее, чем в нисходящей (рабочей). Соответственно, и скорость их должна быть в k раз больше, а чтобы достичь её из неподвижного состояния за то же время, требуется и ускорение во столько же раз большее, чем в нисходящей ветви. Таким образом, хотя в рабочей ветви грузов больше, для разгона обратной ветви нужны бóльшие ускорения и бóльшая сила на каждый элемент. Как и положено по закону рычага, всё это взаимно компенсируется, а если вспомнить про трение и прочие потери, общий результат сразу уходит в минус...
Увы! Закон рычага снова разрушил мираж получения механической свободной энергии с помощью гравитации. Кого я не смог убедить, может начинать договариваться с токарем для изготовления бразильского варианта либо идти за кирпичами и велосипедами для варианта отечественного, чтобы убедиться в этом печальном факте на практике...
Гидравлический ленточный двигатель
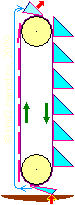
Гидравлический ленточный двигатель.
|
Вот ещё один вариант, во многом подобный рассмотренному выше проекту «лавинного двигателя», но идея доведена до логического завершения — обратная ветвь вообще пустая. Связаться с Нурланом Канатбековым, изобретателем этого ленточного двигателя, можно через его почтовый ящик: nurlan_kanatbekov на mail.ru.
Результат достигается за счёт использования в качестве груза жидкости, а каждый элемент представляет собой складную ёмкость, состоящую из двух пластин, которые могут складываться наподобие книги, и гибкой мембраны между ними (мембрана может быть нерастяжимой или умеренно эластичной). Противоположные ёмкости соединены между собой попарно так, что жидкость может перетекать между ними, причём объём жидкости в каждой паре емкостей достаточен лишь для того, чтобы заполнить одну из них. Элементы прикреплены к надетой на свободно вращающиеся шкивы ленте, в которую как раз могут быть встроены соединяющие их шланги. Шкивы установлены так, что при прохождении элементом нижнего шкива, этот элемент вынужден закрыться и закачать всю воду в противоположный ему элемент, находящийся в самом верху. В результате на рабочей (нисходящей) ветви все элементы всегда наполнены жидкостью, а обратная (восходящая) ветвь вообще пустая. Очевидна огромная разность весов ветвей ленты, которая должна обеспечить превосходный крутящий момент. Также очевидно, что на закрытие одного нижнего элемента будет работать вес всей остальной жидкости, сосредоточенной в нисходящих элементах, а этот вес намного превосходит вес поднимаемой жидкости.
Кажется, работоспособность этой конструкции гарантирована с запасом! Но к сожалению, это только кажется... Конструкция принципиально нерабочая.
Помимо причин неработоспособности, общих для всего этого класса устройств, с точки зрения баланса работ здесь имеется та же проблема, что у рассмотренного выше лавинного двигателя. Если проанализировать работу нисходящей ветви и затраты на поднятие жидкости за один шаг (то есть за период движения ленты, по окончании которого элементы точно занимают места своих предшественников), выяснится, что эти работы равны. Если в нисходящей ветви имеется n элементов, вес каждого из которых равен F, то за этот шаг они совершат работу A = (n · F) · (h / n) = F · h, поскольку эти элементы переместятся лишь на 1/n-ю часть полной высоты h. В то же время вся жидкость из «выжимаемого» внизу элемента должна подняться на полную высоту, для чего необходимо совершить работу против её веса A = F · h (вес перекачиваемой жидкости здесь, как и у прочих элементов, равен F). Получаем точное равенство «полезной» и «вредной» работ, в сумме дающее нулевой выход энергии.
Более того, этот двигатель даже в статике не сможет закрыть нижний элемент! Как только жидкость поднимется на всю высоту до противоположного ему верхнего элемента, давление на нижнюю (закрывающуюся) пластину станет максимальным. И неважно, что масса жидкости в трубке, соединяющей ёмкости, намного меньше массы жидкости, заполняющей даже один элемент — как известно, давление на глубине зависит лишь от высоты столба жидкости и её плотности, но не от массы. Поэтому давление на подвижную пластину будет очень немалое, и чем больше её площадь, тем большая сила потребуется, чтобы закрыть такой элемент, ведь эта сила прямо пропорциональна как давлению, так и площади, на которую это давление действует.
Напрашивается очевидное решение — площадь нужно сделать минимальной, но тогда пропорционально уменьшению площади возрастает ход подвижной пластины-поршня — ведь объём жидкости должен остаться прежним. А на длину этого хода накладываются конструктивные ограничения, поскольку элемент должен закрыться за один шаг ленты, в противном случае в начале следующего шага придётся закрывать уже два элемента — новый и ещё не до конца закрытый старый. Кстати, многие гидравлические аспекты подобной конструкции, в том числе и использование дополнительных грузов для облегчения открытия и закрытия элементов, подробно рассмотрены на этом сайте при анализе водяного колеса с фиксированным краном.
Цепи поплавков в разных средах
Вместо силы тяжести (точнее, вместе с ней), можно попытаться использовать силу Архимеда, погрузив одну из ветвей цепи с поплавками, скажем, в воду, а другую оставив на воздухе или в другой среде с меньшей плотностью (к этим цепочкам поплавков довольно близка и конструкция архимедовой драги). В такой цепи мы получим явный дисбаланс сил, — ведь на погружённую в воду ветвь действует направленная вверх сила всплытия, отсутствующая для ветви, находящейся в воздухе! Но, к сожалению, и тут не всё так просто...
«Полусухая» цепь поплавков
Этой классической идее «вечного двигателя» уже несколько веков. Как говорилось выше, её суть очень проста: если восходящую ветвь с поплавками поместить в воду (рабочий ход), а нисходящую оставить на воздухе, то на поплавок в воде будет действовать как сила тяжести, так и архимедова сила плавучести, выталкивающая его вверх, а на поплавок в воздухе — одна лишь сила тяжести. В результате вес обоих ветвей взаимно компенсируется, а восходящая ветвь дополнительно испытывает нескомпенсированную выталкивающую силу — силу Архимеда, — которая и должна привести всё в движение (кстати, интересный момент: поскольку вес обеих ветвей взаимно скомпенсирован, то в такой конструкции поплавки можно делать как из пенопласта, так и из цельного камня или сплошного свинца — важен не сам вес поплавка, а лишь его объём и соотношение плотностей двух сред — воды и воздуха)!
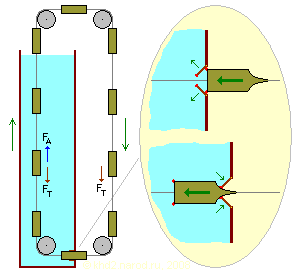 «Полусухая» цепь поплавков на четырёх шкивах (здесь прохождение шлюза легко организовать в самой нижней точке цепи, хотя часто встречаются и варианты подобных конструкций на двух шкивах).
Справа показана форма поплавка, обеспечивающая минимальные потери жидкости при прохождении шторок в нижнем шлюзе; красным обозначены эластичные уплотнения, форма концевой части поплавка является параболой, точные параметры которой зависят от расчётной скорости движения поплавка. Поперечное сечение поплавка и форма шторок предполагаются прямоугольными.
Конечно, практическую реализацию подобного устройства усложняет необходимость установки в нижней части шлюза, если не предотвращающего потери жидкости полностью, то хотя бы сводящего их к приемлемому минимуму. Однако эта задача не является неразрешимой, и один из вариантов такого шлюза показан в правой части рисунка.
Так что же, вечный двигатель изобретён? К сожалению, это не так. Мы забыли про давление, которое надо преодолеть поплавку, чтобы войти через шлюз в нижнюю часть резервуара с водой!
Посчитаем баланс работ на примере одного поплавка в виде прямоугольного параллепипеда, пренебрегая всеми потерями на трение и сопротивление. Баланс состоит из полезной для нас работы выталкивающей силы и вредной работы по преодолению давления воды на нижнем входе в резервуар (напомню ещё раз: действие силы тяжести в обеих ветвях считается взаимно скомпенсированным и потому из рассмотрения исключено).
В соответствии с законом Архимеда, работа выталкивающей силы для одного поплавка равна
АА = h · FA = h · ρ · g · V = h · ρ · g · S · l (1.1),
где АА — работа выталкивающей силы для одного поплавка, выполняемая силой Архимеда; h — высота подъёма поплавка от нижнего шлюза до поверхности жидкости; ρ — плотность жидкости; g — ускорение свободного падения; V — объём поплавка; S — площадь поперечного сечения поплавка; l — длина поплавка.
Работа по преодолению давления воды в нижнем шлюзе равна
АP = l · FP = l · S · P (1.2),
где АP — работа по преодолению давления при входе поплавка в нижнюю часть резервуара с жидкостью; l — длина поплавка (она же длина пути, который поплавок преодолевает, проходя сквозь шлюз); FP — преодолеваемая сила давления воды; S — площадь поперечного сечения поплавка; P — давление жидкости на уровне нижнего шлюза.
В свою очередь, как известно, давление на уровне шлюза вычисляется через высоту столба h и плотность жидкости ρ по формуле P = h · ρ · g. Подставляя это вместо давления в формулу (1.2), мы получаем в точности то же самое выражение, которое фигурировало в формуле (1.1)! Таким образом, работа выталкивающей силы для поплавка в точности равна его работе по преодолению давления жидкости на входе в нижней части резервуара, поэтому даже без учёта дополнительных потерь никакой прибавки энергии здесь не существует в принципе...
Вместо цепи дискретных поплавков можно попытаться использовать что-нибудь непрерывное, скажем надутый (для поддержания формы) шланг. Здесь проблема с уплотнением решается гораздо проще, а главное, не надо преодолевать перепад давления на нижнем входе — ведь сечение такой «цепи» на границе сред в нижней части установки всегда остаётся неизменным. Однако и такой вариант вращаться не будет, причём, на мой взгляд, в случае со шлангом это понятно даже интуитивно — на всём протяжении вертикального участка шланга жидкость давит на него только с боков, взаимно компенсируя своё давление, а нескомпенсированный избыток давления жидкости в нижней части хотя и даст подъёмную силу, но она из-за закона Паскаля не начнёт двигать шланг, а будет компенсирована реакцией опоры (шкива).
Водо-масляная цепь поплавков
А можно ли избежать необходимости преодолевать разность давления на нижнем входе в резервуар, а, стало быть, и необходимости организовывать там шлюз? Можно! Для этого достаточно заменить воздух жидкостью, имеющей меньшую плотность, чем основная, да такой, что эти жидкости не будут смешиваться друг с другом или растворяться друг в друге. Например, можно взять воду и какое-либо жидкое масло и поместить их в половинки сосуда, разделённого вертикальной перегородкой с отверстием возле дна.
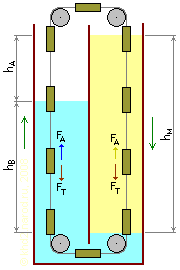 Водо-масляная цепь поплавков по В.И.Богомолову (слева вода, справа масло; вместо двух шкивов показаны четыре для более близкой аналогии с предыдущим рисунком).
В результате более тяжёлая жидкость (в нашем случае — вода) займёт нижнюю часть сосуда и одну из его половин, а более лёгкая (масло) — другую половину. В целях предотвращения занесения поплавками существенного объёма лёгкой жидкости в половину резервуара с тяжёлой жидкостью границу раздела следует сделать несколько выше нижнего края перегородки — это легко осуществить, немного увеличив количество тяжёлой жидкости по сравнению с минимально необходимым. Теперь в результате того, что при постоянном объёме поплавка сила Архимеда прямо пропорциональна плотности жидкости, в которую он погружён, действующая на поплавок сила всплытия в лёгкой жидкости будет меньше, чем в более тяжёлой, в результате чего мы вправе ожидать движения поплавка вверх в тяжёлой жидкости и вниз — в лёгкой. Для наглядности, если взять для поплавка материал, плотность которого является средней между плотностями жидкостей (хотя, как говорилось выше, это и не является обязательным), то в лёгкой жидкости такой поплавок будет тонуть, а в тяжёлой — всплывать.
Законы природы остались прежними, и работа силы Архимеда по-прежнему рассчитывается по формуле
(1.1). Однако в одном случае туда следует подставить параметры для масла hм и ρм, а в другом — для воды hв и ρв. Как же соотносятся между собой взаимно компенсирующие друг друга (ведь давления на границе раздела равны) высоты столбов масла и воды? Совершенно очевидно, что обратно пропорционально их плотностям
Отсюда легко вычислить высоту столба одной жидкости, скажем, масла, через высоту столба другой жидкости: hм = hв · ρв / ρм. Теперь посчитаем работу силы Архимеда для всплытия поплавка в масле (для погружения поплавка там необходимо затратить такую же внешнюю работу):
ААм = hм · ρм · g · V = (hв · ρв / ρм) · ρм · g · V = hв · ρв · g · V (2.2).
Оказалось, что «вредная» для нас работа всплытия в масле в точности равна «полезной» работе всплытия в воде, и потому они взаимно компенсируют друг друга — никакой прибавки работы нет!
Но позвольте, можете сказать Вы, здесь, наверное, ошибка — ведь если поплавок в масле тонет, а в воде всплывает, то дисбаланс сил налицо, и разная высота столбов тут не причём... К сожалению, очень даже причём! Действительно, при прохождении жидкостей поплавок испытывает дисбаланс сил, однако, чтобы устройство начало самовращаться, он должен возвратиться до уровня поверхности наиболее высокого из столбов жидкостей (hм) с положительным запасом энергии. Но для этого он должен преодолеть в атмосфере разность высот между столбами жидкостей hА = hм – hв, а на этом участке на него не действует ничего, кроме тормозящей его подъём силы тяжести. Вот она-то и «съедает» весь накопленный в жидкостях дисбаланс сил, причём, как мы только что выяснили несколько другим путём, «съедает» в точности! Желающие могут проделать расчёты самостоятельно (не забывайте, что считать надо не силы сами по себе, но прежде всего их работы — с учётом пути, на протяжении которого они действуют).
Можно попытаться уравнять высоту столбов жидкостей, но в этом случае мы получим разницу давлений на их границе, а значит, там придётся устанавливать мембрану со шлюзом, и, самое главное, придётся преодолевать эту разницу давлений, — то есть мы приходим к разновидности «полусухого» варианта цепи поплавков.
Впрочем, ничего удивительного в этом нет: по сути, мы опять пытались заставить гравитацию в её двух ипостасях — силы тяжести и силы Архимеда — работать против себя самой. Неудивительно, что в результате мы получили ноль минус затраты на всякие телодвижения...
♦
|