Гидротараный генератор Марухина-Кутьенкова
Этот генератор использует эффект гидроудара — явления, возникающего при резкой остановке потока жидкости в замкнутом объёме (обычно в трубе). При этом из-за практической несжимаемости жидкости её кинетическая энергия преобразуется в ударную волну, распространяющуюся по жидкости от места остановки в обратную сторону и обладающую большой разрушительной силой.
Однако этот эффект не всегда является нежелательным. Уже не одну сотню лет известны и в своё время довольно широко использовались насосы под грозным названием «гидравлический таран», мирно поднимающие воду за счёт энергии потока именно с помощью гидроудара. Они и послужили прототипом гидротараного генератора.
Перебравшиеся в Испанию российские учёные Вячеслав Валентинович Марухин и Валентин Александрович Кутьенков, а также соавтор статей Валентин Иванович Иванов посмотрели на устройство гидравлического тарана по-новому. Это позволило им не только коренным образом изменить работу устройства, полностью устранив потери воды на слив, но и привело к изобретению генератора «свободной энергии». Попробуем проанализировать эту конструкцию, чтобы оценить её возможности.
Модификация гидравлического тарана
От подъёма воды — к генератору энергии
Условия работы и расчёт гидротараного генератора
Энергетический расчёт работы гидротараного генератора
Главное энергетическое условие работы гидротараного генератора
Проверка реальности главного энергетического условия
Гидродинамический расчёт работы гидротараного генератора
Гидроудар в замкнутом пространстве
Расчёт закачки
Расчёт для минимальной нагнетательной камеры
Почему можно уменьшить нагнетательную камеру
Расчёт для экспериментального образца
Работа над ошибками
Вакуум как зеркало для ударной волны?
Причём здесь гравитация?
Необоснованная сверхъединичность
Заключения
Пессимистичное
Оптимистичное
Конспирологическое
Модификация гидравлического тарана
Взяв классический гидравлический таран, изобретатели заглушили в нём слив нагнетательного трубопровода и разместили отбойный клапан между питающим резервуаром и напорным клапаном воздушного колпака. Кажется, изменения невелики, однако они принципиальны — полностью исчез непроизводительный слив из нагнетательной трубы, зато требования к точности расчёта и соблюдению параметров конструкции стали гораздо выше.
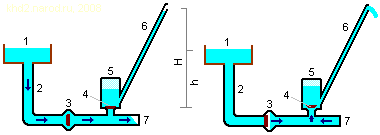 Гидравлический таран с изменённым местоположением отбойного клапана. Слева фаза всасывания (разгона потока), справа — фаза нагнетания (момент гидравлического удара).
1 — питающий резервуар; 2 — нагнетательная труба; 3 — отбойный (ударный) клапан; 4 — напорный (нагнетательный) клапан; 5 — воздушный колпак; 6 — напорная (отводящая) труба; 7 — отсекаемый отбойным клапаном участок нагнетательной трубы (нагнетательная камера — зона рабочего гидроудара). H — высота подъёма воды относительно уровня нагнетения; h — уровень питающего резервуара относительно уровня нагнетения.
Вот как сами авторы описывают его работу (журнал «Альтернативная энергетика и экология», №9 за 2005 г., с.39-46, статья в формате pdf на сайте журнала, см. с.42):
Если этот <отбойный> клапан сделать «обратным» (то есть закрывающимся со стороны трубы 7), при соприкосновении с первой «ударной волной», двигающейся навстречу потоку воды и создающей за собой зону повышенного давления, он получит тенденцию закрыться (от действия разницы давления). При этом начнет перекрывать протекающий через него водяной поток.
Наше исследование такой гидродинамической схемы, введение в теорию механизма открытия и закрытия клапанов с учетом их инерционности, показывает, что при определенной конструкции клапана 3 и определенных исходных параметрах, клапан успеет не только закрыться от первой волны, но останется закрытым, пока действует избыточное давление в трубе 7 под нагнетательным клапаном 4. В итоге, могут создаться условия, когда клапан на некоторое время полностью отсечет водяной поток. При этом отсеченный столб воды в трубе 7, набрав определенную скорость, обязан продолжить свое движение в колпак 5 уже по инерции. Таким образом, сила напора для закачки воды в колпак может быть заменена эквивалентной силой инерции. Однако в отличие от «гидравлического тарана», каждая порция воды, закаченная в колпак, должна вызывать невосполнимые потери массы всего столба воды (поскольку клапан 3 закрыт). Вследствие этого в трубе 7, со стороны закрытого клапана 3, с момента начала движения первой отраженной от него «ударной волны», должна появиться зона разряжения с давлением близким к нулю. В ней может находиться только некоторая малая часть растворенных в воде газов.
Итак, в результате закачки воды в колпак, разность начальной и конечной кинетической энергии перейдет в потенциальную энергию поступившей в колпак воды (как и в «гидравлическом таране»). При этом избыточное давление в колпаке должно запереть нагнетательный клапан, а почти полное отсутствие давления в трубе 7 при разрушении столба воды (если таковой еще в трубе останется), должно открыть клапан 3, находящийся под статическим напором воды со стороны трубы 2. Через открывающийся клапан 3 в трубу 7 опять начнет поступать вода, объем которой за время поступления в точности будет равняться объему зоны «нулевого» давления или, как принято говорить в гидрогазодинамике, зоны «отрыва». При этом параметры воды в трубе при смешении будут определяться соответствующими законами сохранения энергии и импульса.
Более подробные теоретические расчёты с обоснованием работоспособности конструкции, выполненные авторами изобретения, можно найти в их статье «Некоторые теоретические обоснования и экспериментальные доказательства работоспособности нового водоподъёмного устройства как источника экологически чистой энергии» в журнале «Альтернативная энергетика и экология» (№3 за 2006 г., с.41-46), написанной в соавторстве с Валентином Ивановичем Ивановым. Для этого необязательно искать бумажный экземпляр, статья в формате pdf есть на сайте журнала. Должен предупредить, что для тех, кто привык к «классическому» изложению физики, некоторые обозначения и подходы в этой статье окажутся непривычными. В частности, масса воды обозначается символом q, а её удельная плотность называется «удельным весом» и обозначается символом γ. Величину, называемую в статье «энергией», я бы скорее назвал неким «потенциалом», поскольку с «классической» энергией она связана через ускорение свободного падения g: Eв статье = Eв физике / g. Соответственно, и измеряется эта «энергия» не в джоулях, а в кг/м (из-за этого обстоятельства на первый взгляд кажется, что некоторые формулы содержат грубые ошибки; на самом деле таких ошибок нет, только вместо «энергии» там — этот самый «потенциал» в кг/м). Наконец, символами с тильдой (~) в статье обозначены безразмерные доли той или иной величины (кое-где это оговорено явно, кое-где об этом приходится догадываться лишь из логики рассуждений и математики).
Вышеприведённое описание работы новой конструкции достаточно подробное, однако всё-таки ещё раз выделю наиболее существенные моменты, которые подчёркивают авторы конструкции.
-
Клапан 3 должен иметь специальную конструкцию. Простая лёгкая заслонка с пружиной, исправно работавшая в классическом гидравлическом таране, откроется тут же при возникновении «зоны отрыва», поскольку со стороны трубы 7 будет разрежение, близкое к вакууму, а со стороны трубы 2 — зона повышенного давления, так как с той стороны в этот момент может быть повторный цикл гидроудара или, если этот гидроудар уже затухнет, то гидростатическое давление с той стороны всё равно будет заведомо больше, чем «давление» вакуума в зоне отрыва. Но клапан 3 должен оставаться закрытым всё время, необходимое для того, чтобы в колпак 5 из трубы 7 перешло максимально возможное количество воды.
-
Условием длительного повторения рабочих циклов является требование точного равенства объёма воды, поступающего в трубу 7 через отбойный клапан 3 в фазе разгона потока, и поступающего из трубы 7 в колпак 5 через напорный клапан 4 в фазе гидроудара (при закрытом отбойном клапане 3). При этом вода в отсекаемой части нагнетательной трубы должна успеть получить достаточный запас энергии, чтобы снова подать такой же объём воды в колпак 5, преодолев все разности давлений и неизбежные потери на гидравлическое трение.
Запомним эти моменты, но пока продолжим следить за мыслью авторов.
От подъёма воды — к генератору энергии
Итак, в модифицированной установке отсутствует слив из нагнетательной трубы. Это значит, что один из главных недостатков гидравлического тарана — необходимость обеспечения свободного выхода воды из нагнетательной трубы в фазе разгона потока — преодолён. Теперь ничто не мешает погрузить установку в стоячий водоём. А раз так, то нет необходимости и в особом питающем резервуаре и наклоне нагнетательной трубы — питающим резервуаром будет весь водоём, в который погружена установка, а нагнетательную трубу можно сделать горизонтальной, поскольку необходимое для работы давление будет обеспечивать глубина размещения входа в эту трубу в толще водоёма. Правда, совсем отказаться от нагнетательной трубы нельзя — её стенки формируют направленный поток, обеспечивающий гидроудар, отделяя его от общей массы воды в водоёме.
Наконец, можно разместить горизонтально и отводящую трубу, сократив её длину и превратив в насадок на выходном отверстии колпака. При этом давление, ранее поднимавшее воду наверх, теперь будет создавать горизонтальную струю воды, выходящую из этого насадка. Эту струю можно использовать для реактивного движения установки, если она не закреплена на дне, либо, наоборот, можно закрепить установку, а струю использовать для вращения турбины, совершающей какую-либо полезную работу, скажем, вращающую электрогенератор.
Модифицированное таким способом устройство приобретает вид, показанный на следующем рисунке.
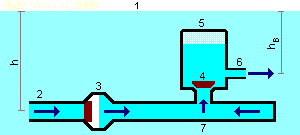 Гидротараный генератор водяной струи.
1 — поверхность водоёма (начало отсчёта глубины); 2 — нагнетательная труба; 3 — отбойный (ударный) клапан; 4 — напорный (нагнетательный) клапан; 5 — воздушный колпак; 6 — выходной насадок; 7 — отсекаемый отбойным клапаном участок нагнетательной трубы (зона рабочего гидроудара). h — глубина размещения нагнетательной трубы (напор на входе этой трубы); hв — глубина размещения выходного насадка (напор среды на выходе).
В результате произведённых расчётов авторы пришли к выводу, что минимальная глубина, на которой может работать такая система — 15 метров. Точнее, минимальное давление на входе нагнетательной трубы должно быть не меньше 2.5 атм в абсолютном исчислении (относительно вакуума) или 1.5 атм относительно давления воздуха на уровне моря. Вакуум мною упомянут не случайно, так как во время работы установки там есть либо давление, соответствующее глубине погружения (в воздушном колпаке) или большее (в момент гидроудара), либо пустота, временно образующаяся в зоне отрыва. Авторы предупреждают, что меньшая глубина с учётом свойств реальных материалов не обеспечит нужной скорости потока и необходимой энергии гидроудара, а также должного режима работы клапанов.
Условия работы и расчёт гидротараного генератора
Какие же физические условия должны выполняться для успешной работы гидротараного генератора? Прежде всего, как уже говорилось выше, объём воды, поступающей в отсекаемую область нагнетательной трубы в фазе разгона должен быть в точности равен объёму воды, вытесняемой в результате гидроудара в колпак и отводящую трубу. Но для того, чтобы обеспечить это условие, надо выполнить ещё пару пунктов.
-
Гидроудар должен быть весьма сильным, чтобы образовалась достаточно большая пустая зона отрыва, в которой вода будет разгоняться во время следующего рабочего цикла.
-
При разгоне до момента отсечки отсекаемая часть потока должна успеть набрать кинетическую энергию, как минимум достаточную для преодоления водой, добавленной в отсекаемый фрагмент трубы, разности давлений между уровнем отсечения напорной трубы и уровнем выхода отводящей трубы. На первый взгляд кажется, что это условие нарушит закон сохранения энергии. Попробуем проверить, так ли это?
Энергетический расчёт работы гидротараного генератора
Главное энергетическое условие работы гидротараного генератора
Как известно, кинетическая энергия потока определяется по формуле
где EK — кинетическая энергия; mT — движущаяся масса, если заполняемая пустота была возле заглушки, то это масса всей отсекаемой отбойным клапаном жидкости; v — скорость движения этой жидкости в момент отсечения.
В то же время для подъёма жидкости на нужную высоту и преодоления соответствующей разности давлений необходима энергия
где EП — потенциальная энергия, или энергия напора; mН — поднимаемая масса, в данном случае это масса нагнетённой жидкости, прошедшей напорный клапан; g — ускорение свободного падения; h — высота подъёма.
Кажется, что это очередной механический «вечный двигатель», конструкция заведомо нерабочая. Однако есть и пара нюансов. Во-первых, через напорный клапан никогда не пройдёт вся жидкость, часть её обязательно останется в нагнетательной трубе. Поэтому всегда соблюдается условие
mТ > mН, которое скорее всего можно записать как mТ >> mН (1.3).
Во-вторых, разгон осуществляется не за счёт «рабочей» энергии, отбираемой на выходе устройства, а внешним давлением окружающей жидкости, которое можно считать практически неизменным даже в случае не слишком большого объёма водоёма — ведь при установившемся режиме работы количество жидкости, поступающей в установку через вход нагнетательной трубы, в точности равно количеству жидкости, которую установка отдала обратно через выходной насадок, поэтому общий объём жидкости в водоёме остаётся прежним и, следовательно, не меняются ни его уровень, ни давление на глубине размещения установки.
Таким образом, с точки зрения баланса энергий без учёта потерь всё сводится к тому, что в начале очередного цикла в отсекаемой части нагнетательной трубы должно быть достаточно свободного места, чтобы заполняющий её поток успел набрать скорость
v > √(2 · g · h · mН/ mТ) (1.4),
где v — необходимая минимальная скорость потока; √ — операция извлечения квадратного корня; g — ускорение свободного падения; h — высота подъёма; mT — масса всей жидкости, отсекаемой отбойным клапаном; mН — масса нагнетённой жидкости, прошедшей напорный клапан за один цикл разгона-нагнетения.
Это и есть главное условие успешной работы гидротараного генератора.
Из формулы (1.4) следует вывод, что чем меньшая доля отсечённой жидкости пройдёт напорный клапан, тем меньшая скорость отсекаемого потока будет нужна. Но, с другой стороны, для разгона потока требуется место в отсекаемой части нагнетательной трубы, а значит, объём жидкости, вытесненной через напорный клапан в отводящую трубу, должен быть достаточно заметным.
Проверка реальности главного энергетического условия
Посмотрим, реально ли выполнить это условие? С помощью программы SiP выполним расчёт скорости потока воды при 20°С, разгоняющегося под воздействием внешнего гидростатического давления 0.3 МПа (глубина 20 м + атмосферное давление) в трубе, частично пустой (вакуум), а частично заполненной такой же водой. Примем длину трубы равной 10 м, внутренний диаметр — 10 см, материал — сталь. Расчёт проведём для трёх разных ситуаций — неподвижная вода сосредоточена у входа, а пустота, которую надо заполнить — у заглушки; обратная ситуация — вода сосредоточена возле заглушки, а пустота у входа; и, наконец, вода сосредоточена по краям, а пустота — в центре трубы.
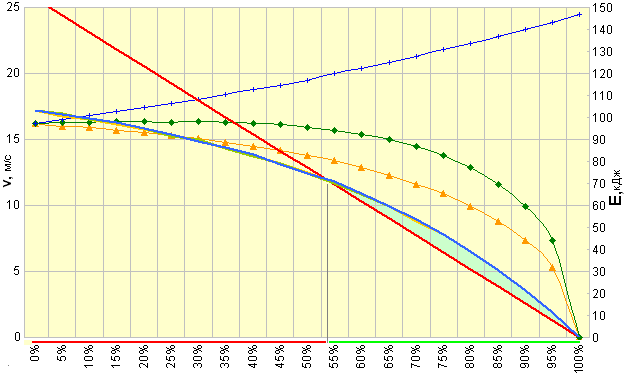 Зависимость скорости и кинетической энергии заполняющей трубу воды от степени её предварительного заполнения.
По горизонтали указана степень предварительного заполнения трубы неподвижной водой — от 0% (изначально пустая труба) до 100% (полностью заполненная).
Линии с маркерами — результаты расчёта скорости (жёлтая — заполняемая пустота сосредоточена у заглушки, зелёная — пустота в центре трубы, синяя — заполняемая пустота возле входа в трубу). Красная линия — энергия, необходимая для подъёма заполняющей порции воды до уровня поверхности (на 20 м). Жёлтая, зелёная и синяя линии без маркеров (взаимно перекрываются) — кинетические энергии воды в трубе в момент её заполнения для соответствующих ситуаций.
Сами по себе графики скорости не содержат в себе чего-либо необычного. Понятно, что когда надо разгонять неподвижную воду (пустота у заглушки или в середине трубы), то чем меньше заполняемое пространство (зона разгона) и чем больше доля изначально неподвижной воды, тем меньше будет скорость в момент полного заполнения трубы. Наоброт, если вся пустота сосредоточена у входа, то единственное, что мешает заполняющему потоку — это гидравлическое трение, и чем оно больше, то есть чем больший путь надо пройти воде, тем больше потери и меньше конечная скорость.
Даже когда вычисленные кинетические энергии при полном заполнении трубы (с учётом доли именно движущейся в этот момент жидкости), совпали друг с другом с точностью до погрешности численных методов, использованных для вычисления скорости потока, это не вызвало особого удивления — в конце концов, так и должно быть, для потенциальной энергии и произведённой с её помощью работы (но не для скорости!) безразлично, в каком именно конце горизонтальной трубы находится заполняемая пустота — ведь потенциал этой пустоты одинаков, глубина-то одна и та же. «Сенсация» обнаружилась после того, как я наложил на графики кинетических энергий график потенциальной энергии, необходимой для подъёма заполнившей трубу порции воды на поверхность, то есть на 20 м (наклонная красная линия). Для предварительного заполнения 55% и больше он прошёл ниже графика кинетической энергии, а это значило, что энергия отсечённой воды больше, чем надо для её подъёма. Стало быть, выполняется условие (1.4), и здесь действительно возможно получение энергии, по сути, «из ничего»! На рисунке эта область отмечена зеленоватой закраской и зелёной линией вдоль горизонтальной оси.
Пора закупать трубы? Однако радость длилась недолго — ведь при подаче воды через напорный клапан в трубе образуется вакуум, а стало быть, поднимаемая вода должна преодолеть не только 20 м вверх, но и атмосферное давление, эквивалентное ещё примерно 10 м водяного столба. В самом деле, ведь при определении разгоняющего давления мы учли вакуум в трубе, добавив к гидростатическому давлению на глубине 20 м ещё и 0.1 МПа атмосферного давления, значит, то же самое надо сделать и при расчёте подъёма воды! Результаты, пересчитанные с учётом этой добавки, принесли разочарование.
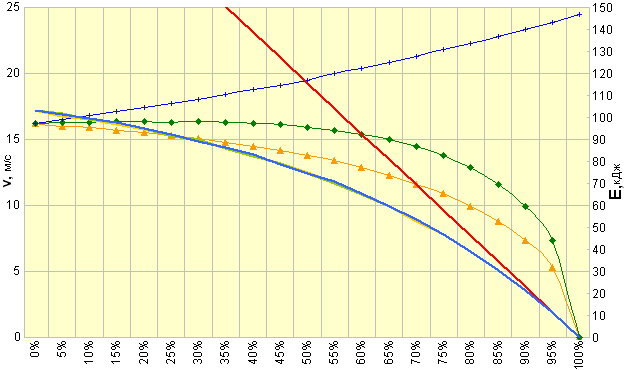 Зависимость скорости и кинетической энергии заполняющей трубу воды от степени её предварительного заполнения. Энергия, необходимая для обратного подъёма заполняющей порции (красная линия), показана с учётом необходимости преодоления атмосферного давления.
Теперь график потенциальной энергии образует касательную к графику кинетической энергии, не пересекая его и не давая тем самым надежд на «дополнительную» энергию — в полном соответствии с классическим законом сохранения энергии.
Таким образом, вместо расчёта потенциальной энергии по формуле (1.2) следует рассчитывать работу подъёма как
AП = mН · (g · h + P / ρ) (1.5),
где AП — минимальная работа по подъёму нагнетаемой воды; mН — поднимаемая масса, в данном случае это масса нагнетённой жидкости, прошедшей напорный клапан; g — ускорение свободного падения; h — высота подъёма; P — давление на выходе из напорной трубы; ρ — удельная плотность жидкости.
Соответственно, и главное условие успешной работы гидротаранного генератора вместо формулы (1.4) должно записываться как
v > √((2 · g · h + P / ρ) · mН/ mТ) (1.6),
где v — необходимая минимальная скорость потока; √ — операция извлечения квадратного корня; g — ускорение свободного падения; h — высота подъёма; P — давление на выходе из напорной трубы; ρ — удельная плотность жидкости; mT — масса всей жидкости, отсекаемой отбойным клапаном; mН — масса нагнетённой жидкости, прошедшей напорный клапан за один цикл разгона-нагнетения.
Контрольные расчёты для других давлений — от 0.1 МПа (1 атм, глубина 10 м) до 10 МПа (100 атм, глубина 1000 м) дали такие же результаты — выигрыша энергии нет, а с ростом давления и скорости заполнения лишь увеличиваются гидравлические потери!
Впрочем, это и не удивительно. Ведь физическая модель, используемая применёнными численными методами расчёта, основана в конечном счёте на уравнении Бернулли. Поэтому и результаты «на круг» за вычетом гидродинамических потерь сходятся практически в ноль. Это говорит о том, что все вычисления проводятся корректно — ведь уравнение Бернулли по своей сути является энергетическим и содержит два потенциальных члена (собственно потенциал и давление) и один кинетический (скоростной напор), а потому и должно давать нулевой результат в замкнутом цикле. Правда, остаётся вопрос, правомерно ли применение уравнения Бернулли в данных условиях? Однако я не вижу причин его неприменимости, да и хорошая корреляция с результатами расчёта по формуле C.Д.Чистопольского говорит об оправданности такого подхода.
Гидродинамический расчёт работы гидротараного генератора
Попытка энергетического расчёта не дала положительного результата. Но, может быть, здесь действуют другие законы, и классический энергетический подход неприменим — мы не учли какие-либо факторы? Попробуем смоделировать возможные процессы с чисто гидродинамических позиций.
Гидроудар в замкнутом пространстве
Есть ли отличие сильного гидроудара, необходимого для работы гидротаранного генератора, происходящего в замкнутом участке трубы (нагнетательной камере) от такого же «классического» гидроудара, происходящего в трубе с открытым входом? Отличие есть, и весьма важное.
При открытом входе стадия отбоя сильного гидроудара длится существенно дольше стадии сжатия. Это обусловлено тем, что жидкость через вход трубы выходит в открытое пространство и там её инерция гасится относительно невысоким по сравнению со стадией сжатия внешним давлением, которое затем также неспешно «заталкивает» её обратно, заполняя образовавшуюся у заглушки зону отрыва.
Когда нагнетательная камера замкнута со всех сторон, отброшенная от заглушки жидкость не может выйти во внешнее пространство, а упирается в закрытый отбойный клапан. И если жёсткость этого клапана такая же, как у заглушки, он действует также жёстко и резко, как заглушка. Поэтому тут же возникает встречный гидроудар, вновь отбрасывающий жидкость к заглушке. В результате жидкость попеременно испытывает два гидроудара — то у заглушки, то у закрытого клапана. При этом относительно каждого из них длительности стадий сжатия и разрежения равны — ведь нагнетательная камера заполнена полностью и энергия (ударная волна) лишь перекатывается от заглушки к клапану и обратно без существенного перемещения жидкости. Если отбойный клапан закрылся в тот момент, когда жидкость только начала испытывать разрежение (и при этом удалось избежать какого-либо изменения объёма отсекаемой им нагнетательной камеры), то длительность стадии разрежения может быть и меньше длительности стадии сжатия — пропорционально тому объёму жидкости, который успел испытать падение давления. Наконец, если бы удалось захлопнуть отбойный клапан вообще без потерь давления гидроудара и объёма отсекаемой камеры, то мы получили бы «консервированный гидроудар» — объём жидкости в замкнутом сосуде под давлением, соответствующим скачку давления гидроудара и без каких-либо волн давления в её объёме, — как если бы жидкость просто закачали бы в эту камеру под таким давлением. Но стоит приоткрыть клапан — и мы сразу «расконсервируем» гидроудар, начиная с фазы 4.
Однако в случае, когда образуется увеличивающееся свободное пространство, скажем, из-за утечки, вызванной нагнетанием жидкости в воздушный колпак, картина меняется. Стадия разрежения становится длиннее на время, которое жидкости необходимо для того, чтобы пересечь зону отрыва в одну сторону при отбое, а затем снова вернуться обратно при следующем ударе. Но практически всегда это происходит намного быстрее, чем в случае открытого входа в трубу — ведь возвратное движение обеспечивается не мягким воздействием внешнего давления, а жёстким гидроударом о противоположную стенку закрытой камеры.
Таким образом, в замкнутой нагнетательной камере частота повторных гидроударов гораздо выше, чем та же частота в трубе с открытым входом, а стало быть, выше эффективность закачки. Правда, по мере закачки воды возрастает зона отрыва, а это приводит к снижению частоты повторных гидроударов в отличии от трубы с открытым входом, где частота повторных гидроударов по мере снижения их силы возрастает до тех пор, когда гидроудар перейдёт в категорию «слабых» и период повторных циклов стабилизируется.
Расчёт закачки
Возьмём те же параметры трубы, что и при энергетическом расчёте, — вода при 20°С, глубина 20 м и стальная труба длиной 10 м с толщиной стенки 5 мм и внутренним диаметром 10 см, частично заполненная той же водой.
В таблице приведены результаты расчёта закачки для исходного 90%-го заполнения нагнетательной трубы при разных сечениях отверстия напорного клапана с учётом противодавления в воздушном колпаке 0.3 МПа (3 атм) и в предположении, что напорный клапан находится в заглушенном торце нагнетательной трубы. Время разгона до гидроудара для изначально неподвижной заполняющей воды составит 254 мс, а скорость в нагнетательной трубе в момент гидроудара при этом будет 7.38 м/с (скачок давления — до 9.87 МПа, т.е. 100.0 атм). При скорости ударной волны 1.34 км/с длительность этапа сжатия будет около 15 мс. Длина стального напорного патрубка, по которому вода поступает из нагнетательной трубы в воздушный колпак, принята равной удвоенной толщине стенки трубы — 1 см. Потери во время возврата отбойной волны при повторных гидроударах не учитываются.
В связи с большим объёмом данных подробные результаты расчёта представлены на отдельной странице. Здесь приведены лишь суммарные результаты для всех повторных гидроударов в течении одного такта работы генератора.
| Диаметр напорного клапана |
1 см |
2 см |
5 см |
9 см |
| Количество закачивающих гидроударов |
6 |
2 |
11 |
16 |
| Общее время закачки |
478 мс |
165 мс |
165 мс |
225 мс |
Продвижение воды в нагнетательной трубе
Закачанный объём
|
5.4 cм
424 мл |
5.7 cм
448 мл |
50.0 cм
3.93 л |
84.3 cм
6.62 л |
Эти результаты тоже не радуют — при диаметре напорного отверстия чуть более 2 см утечки следует рассматривать как большие и обратного движения воды, а следовательно и повторных гидроударов в одном такте работы такой установки ждать не приходится (в данном случае число гидроударов в таблице — это число этапов единого продолжительного затухающего гидроудара), а при меньших значениях повторные гидроудары в одном такте возможны, но нагнетаемый каждым из них объём слишком мал, а затухание из-за закачки слишком велико, чтобы можно было ожидать освобождения в нагнетательной трубе объёма, достаточного для повторного такта такой же силы (напомню, это должно быть 10% от 10 м — то есть 100 см нагнетательной трубы).
Глядя на подробные данные, видно, что при больших диаметрах напорного клапана мы имеем гидроудар с большими утечками без отбойного движения. И именно для этих случаев расчёт показал наименьшее повышение давления и наибольший закачанный объём. А ведь этот результат, на первый взгляд парадоксальный, вполне логичен. Дело в том, что для закачки воды в воздушный колпак нам надо преодолеть всего лишь его противодавление — 0.3 МПа. Прочий избыток давления расходуется на ненужный разгон воды, превращаясь в её кинетическую энергию, которая рассеивается при разрушении нагнетаемой струи в воздушном колпаке. Поэтому чем меньше избыток давления, тем более эффективно используется энергия для совершения полезной работы (закачки) и тем меньше её теряется на бесполезный разгон воды до огромных скоростей. В пределе, когда сечение напорного клапана равно сечению нагнетательной трубы, мы получим как раз то, что весь скоростной напор отсечённого потока, полученный при разгоне его внешнем давлением 0.3 МПа истратится на преодоление точно такого же противодавления в воздушном колпаке (правда, в реальности будут ещё и различные виды потерь).
А как согласуются полученные результаты с классической формулой Чистопольского? Считая скорость в конце закачки весьма близкой к нулю (vK = 0), независимо от сечения напорного клапана мы получим, что должно быть закачано v0 / c = 7.38 / 1340 = 0.0055 = 0.55% от общего объёма нагнетательной камеры, что соответствует продвижению воды в трубе на 5.5 см. Сравнив этот результат с вышеприведённой таблицей, мы видим, что он хорошо соответствует случаям гидроударов с малыми утечками и явным отбойным движением, когда сечение напорного клапана относительно невелико (суммарное расчётное продвижение 5.4 см и 5.7 см). В случае же «размазанных» гидроударов он даёт гораздо меньшие значения. Это связано с тем, что в этой формуле, по сути, жёстко зашита «стандартная» длительность гидроудара, а в случае гидроудара с большими утечками она как бы «размазывается», и их длительность существенно возрастает.
Расчёт для минимальной нагнетательной камеры
И всё же... Почему мы взяли длину отсекаемой отбойным клапаном части трубы (нагнетательной камеры) 10 м? Лишь потому, что эта длина является минимально оптимальной для классических гидротаранов, поскольку обеспечивает приемлемую длительность этапа сжатия гидроудара — чтобы успели сработать клапаны и осталось достаточное время для нагнетания хоть сколько-нибудь существенного объёма жидкости!
Почему можно уменьшить нагнетательную камеру
Однако здесь у нас не гидротаран, где открытый входной конец трубы требует, чтобы каждый цикл гидроудара полностью проходил все стадии рабочего цикла, и в каждом такте работы происходил бы только один гидроудар без повторных циклов. Наоборот, здесь авторы особо подчёркивают то обстоятельство, что отбойный клапан закрывается и после этого в отсечённом пространстве происходит множество гидроударов, что и обеспечивает работу этого устройства! Поэтому нам совсем необязательно иметь столь длинную отсекаемую часть, — она не даст выигрыша в энергии, а перемещение жидкости по ней туда-сюда при повторных циклах гидроудара в пределах одного такта и разгон инертной воды при открытии лишь вызовут дополнительные потери.
Поэтому можно попробовать ограничиться отсечением нагнетательной камеры, объём которой должен быть практически полностью закачан в воздушный колпак. При этом следует лишь обеспечить закрытие отбойного клапана первой же обратной волной, что вполне возможно с учётом достаточно высокого давления при гидроударе. О том, что напорный клапан не будет успевать закрываться между повторными циклами гидроудара, можно сильно не переживать, — ведь при достаточной силе основного гидроудара противодавление в воздушном колпаке во много раз меньше скачка давления гидроудара и потому не успеет вытолкнуть обратно в нагнетательную камеру существеного объёма жидкости. Скорее всего, не будет вытолкнуто вообще ничего, поскольку жидкость из нагнетательной камеры проталкивается в воздушный колпак с большой скоростью и имеет существенную инерцию, которую относительно слабое противодавление не успеет погасить, не говоря уже о том, чтобы повернуть вспять. Единственное условие — слой воды над напорным клапаном должен быть достаточно большим, чтобы не позволить воздуху из воздушного колпака проникнуть через напорный клапан в нагнетательную камеру.
Всё было бы хорошо, если бы не одно «но». В начале такта нагнетательная камера предполагается пустой. Поэтому заполняющая её вода хлынет туда с максимально возможной скоростью, которая, как известно, равна
vМ = √(2 · P / ρ) = √(2 · g · h) (2.1),
где vМ — максимальная скорость потока; √ — операция извлечения квадратного корня; ρ — удельная плотность жидкости; P — давление в данном месте; g — ускорение свободного падения; h — высота столба жидкости в данном месте.
Поэтому кинетическая энергия, полученная жидкостью при заполнении нагнетательной камеры, будет в точности равна работе, которую необходимо совершить для её возвращения на высоту h. Выигрыша не видно, зато потери на трение неизбежны...
Расчёт для экспериментального образца
В своей статье в журнала «Альтернативная энергетика и экология» (№3 за 2006 г., pdf) на с.45 авторы дают весьма подробные сведения о результатах проведённого ими эксперимента, в частности, говорится следующее:
По результатам испытаний малогабаритного энергетического модуля, <...> при конструктивных параметрах: LH = 1 м, h = 50 м, S0 = 0,0314 м2 и расчётных параметрах: δqH = 0,938 и NT/S0 = 3102 кВт / м2 было экспериментально получено: H - h = 31,53 м, NT = 92,73 кВт, tH = 0,068 c.
Мощность турбины NT нас пока мало интересует, а вот остальные параметры вполне заслуживают внимания, и прежде всего доля нагнетаемой жидкости δqH = 0.938, то есть в нагнетательной камере остаётся всего 6.2% от попавшего туда во время разгона объёма воды, всё остальное должно попасть в напорный колпак. Это как раз случай нагнетательной камеры минимальных размеров, поэтому, невзирая на сделанный в предыдущем пункте вывод, всё же проведём расчёт, благо все принципиально важные данные известны: длина трубы 1 м, её внутренний диаметр — 20 см, глубина 50 м (давление разгона с учётом вакуума — 0.6 МПа, противодавление в воздушном колпаке такое же). Примем в качестве материала трубы сталь с толщиной стенки 2 см (чтобы была жёстче), удельная плотность океанской воды при 20°С — 1030 кг / м3.
Сначала с помощью программы SiP рассчитаем скорость потока в момент гидроудара при заполнении нагнетательной трубы, в которой имеется 6.2% неподвижной воды (это 62 мм предварительного заполнения, сосредоточенного, скажем, у входа в трубу, — тогда результат не надо будет нормировать к доле движущейся воды, поскольку к моменту заполнения движется вся вода). По результатам расчёта при прохождении потоком отметки 1 м от входа в трубу он разгонится до 32.4 м/с и произойдёт это за 32.4 мс. При этом скорость звука в воде составит 1.46 км/с, а скорость ударной волны — лишь 1.38 км/с, то есть время прохождения ударной волны по трубе будет примерно 0.14 мс, туда-обратно (длительность стадии сжатия у заглушки) — 0.28 мс. При отсутствии утечек давление первичного гидроудара может превысить 46 МПа (более 450 атм).
Теперь заполним таблицу с результатами гидроудара для разных соотношений просвета напорного клапана и внутреннего сечения нагнетательной камеры, считая длину патрубка между нагнетательной трубой и воздушным колпаком минимальной и равной толщине стенки нагнетательной трубы (2 см). При этом считаем, что вода в воздушном колпаке вообще не мешает поступать новым проциям, потери при сужении канала течения воды при переходе из нагнетательной трубы в напорный патрубок и потери при перемещении воды в нагнетательной камере туда-сюда не учитываем. В качестве критерия окончания закачки логично выбрать снижение давления гидроудара ниже противодавления в воздушном колпаке (0.6 МПа).
В связи с большим объёмом данных подробные результаты расчёта представлены на отдельной странице. Здесь приведены лишь суммарные результаты для всех повторных гидроударов в течении одного такта работы генератора.
| Диаметр напорного клапана |
1 см |
2 см |
5 см |
10 см |
19 см |
| Количество закачивающих гидроударов |
45 |
11 |
4 |
13 |
30 |
| Общее время закачки |
183 мс |
61.4 мс |
2.64 мс |
3.64 мс |
8.40 мс |
Продвижение воды в нагнетательной трубе
Закачанный объём
|
4.54 мм
143 мл
(0.45%) |
4.51 мм
142 мл
(0.45%) |
5.24 мм
165 мл
(0.52%) |
33.0 мм
1036 мл
(3.3%) |
110 мм
3456 мл
(11%) |
Результаты получились гораздо хуже, чем в случае для большой 10-метровой трубы с расчётной закачкой 10% от её объёма. Попробуем проанализировать, почему это так?
Дело в том, что здесь у нас нет «инертных» 90% воды, не позволяющих ускоряемой воде развить слишком большую скорость, но зато обеспечивающих большую длительность гидроудара по сравнению с нагнетательной камерой минимального размера. В маленькой камере начальная скорость и скачки давления гораздо выше, а значит, выше и связанные с этим бесполезные потери на совершенно ненужный здесь разгон нагнетаемой гидроударом воды до сверхвысоких скоростей.
Таким образом, минимизация нагнетательной камеры и уменьшение сечения напорного клапана и перепускного патрубка между нагнетательной камерой и воздушным колпаком лишь снижает эффективность закачки. Это неминуемо должно было проявиться в ходе экспериментов.
Следует отметить, что расчёт по Чистопольскому с учётом условия нулевой кинетической энергии в конце (vK = 0) независимо от сечения напорного клапана даёт v0 / c = 32.4 / 1380 = 0.0235 = 2.35% от общего объёма нагнетательной камеры, что соответствует продвижению воды в трубе на 23.5 мм. Это не соответствует первым трём столбцам таблицы, содержащим близкие друг к другу результаты (как раз там имеют место множественные повторные гидроудары с выраженными отбойными движениями). Однако я должен заметить, что формула Чистопольского предназначена для гидравлических таранов, в которых, как известно, нагнетается лишь относительно малая часть от всей воды, находящейся в трубе, и предполагаются относительно небольшие скорости потоков. Здесь же мы имеем дело с очень высокой скоростью потока и соответствующими ей огромными потерями. Очевидно, именно это обстоятельство и «съедает» почти 80% от результата Чистопольского.
Кстати, близкое к приведённому в статье время нагнетения у нас получилось для напорного клапана диаметром 2 см, однако объём закачки в этом случае в 200 раз меньше требуемого. Это слишком вопиющее расхожденние!
Работа над ошибками
Почему же у нас не получилось полезного выхода энергии? Ведь в упомянутой статье из журнала «Альтернативная энергетика и экология» (№3 за 2006 г., с.41-46, pdf), авторы изобретения тоже вроде бы исходят из известных законов сохранения массы, энергии и импульса, используют в качестве базовых многократно апробированные формулы, да и выкладки выглядят вполне логично, но у них получается прибавка, а у нас нет?
Впрочем, несколько настораживает тот факт, что, с одной стороны они опираются на закон сохранения энергии, а с другой, получают прибавку энергии, так и не указывая, за счёт чего (если причины известны) или на каком этапе (если причины неизвестны) она получается. А прибавка несомненна — вся вода возвращается обратно, уровень её не меняется, а дополнительная полезная работа откуда-то берётся! С чего бы это? Вчитаемся в статью более внимательно.
Вакуум как зеркало для ударной волны?
Первое, что бросается в глаза, — это описание отражения ударной волны от границы воды с вакуумом (с.41-42). Цитата:
...в новой гидродинамической схеме каждая порция воды, закачанная в колпак в отличие от «гидравлического тарана», поскольку ударный клапан закрыт, будет вызывать невосполнимые потери массы всего продолжающего двигаться по инерции в направлении к нагнетательному клапану столба воды. Вследствие этого в нагнетательной трубе со стороны ударного клапана уже с момента начала движения первой отраженной «ударной волны» должна появиться зона разрежения с давлением близким к нулю, в которой может находиться только некоторая часть растворенных в воде газов, или должна появиться «зона отрыва» (гидродинамический термин). Размер этой зоны во время закачки воды в колпак будет увеличиваться. В результате все последующие отражения «ударной волны» в направлении нагнетательного клапана будут происходить не от ударного клапана, а от «зоны отрыва». При этом каждая порция закачиваемой воды из-за уменьшения продолжительности действия давления под нагнетательным клапаном, будет уменьшаться.
То, что после каждого такта нагнетения порция воды в нагнетательной камере будет уменьшаться, а зона пустоты будет увеличиваться — несомненно. То, что в связи с этим длительность такта нагнетения и объём нагнетаемой порции будет сокращаться — тоже очевидно. Но вот то, что ударная волна будет отражаться не от ударного клапана, а от «зоны отрыва» — неочевидно абсолютно, и мягко говоря, весьма сомнительно. Механическая энергия не может отразится от пустоты. Она может отразится (и весьма резко) от границы раздела сред — за счёт реакции другой среды, может «отразится» от горизонтальной границы раздела жидкости и воздуха или вакуума, хотя в этом случае процесс только выглядит как отражение, — на самом деле жидкость поднимется в воздух (плавным куполом или столбом брызг — зависит от формы и силы ударной волны возле поверхности), но в данном случае энергию вернёт обратно в воду не мизерная реакция воздуха, а сила тяготения, аналогично тому, как при повторных гидроударах в трубе с открытым входом энергию в трубу возвращает давление внешней жидкости. Но вертикальная граница (ведь в приведённой схеме гидротаранного генератора труба-то расположена горизонтально!) между жидкостью и пустотой не может остановить механическое движение жидкости, потому что пустоте просто нечем воспрепятствовать ему.
Единственное, что может затормозить движение жидкости в пустоте — это силы поверхностного натяжения и силы смачивания стенок трубы. Однако при размерах, измеряемых сантиметрами, и скоростях, измеряемых метрами в секунду, влияние этих сил практически незаметно. Убедиться в этом может каждый, капнув на стол каплю воды диаметром в несколько миллиметров с высоты в пару десятков сантиметров — ничто не мешает ей разлететься брызгами в разные стороны (вот когда размеры измеряются микрометрами, тогда влияние этих сил, пропорциональных площади поверхности, становится не просто существенным, но и определяющим — силы инерции и упругой объёмной деформации, зависящие от массы и объёма, по сравнению с ними ослабевают в той же степени, в какой уменьшаются линейные размеры).
Поэтому при повторных гидроударах вода в данном случае отражается именно от закрытого ударного клапана, болтаясь по всей нагнетательной камере туда-сюда. Впрочем, это обстоятельство в дальнейшем явно нигде не учитывается, но при конструировании клапанов будет очень важным. Кроме того, при «отражении от вакуума» частота повторных гидроударов должна возрастать (при сокращении длительности каждого из них), а сила их оставаться прежней. Если же происходит отражение от ударного клапана, то частота гидроударов не может увеличиваться (ведь длина нагнетательной камеры не уменьшается), а из-за падения скорости при повторных гидроударах должна даже уменьшаться.
Дополнение. Должен покаяться — лишь через пару месяцев меня осенило, что таким образом авторами был описан механизм гидроудара с большими утечками. В этом случае, действительно, «зона отрыва» возникает у закрывшегося клапана в нагнетательной трубе, а зона изменения давления (то есть «ударная волна») как бы «отражается» от вакуума. Но именно «как бы отражается», поскольку на самом деле физика процесса не имеет ничего общего с обычным отражением-отбоем, а заключается в некотором «сбросе давления» в движущейся жидкости за счёт снижения скорости движения её части, граничащей с вакуумом. Движение границы этой «подторможенной» зоны в сторону заглушки внешне выглядит как «отражение» ударной волны от вакуума с одновременным её ослабеванием. При этом на каждом такте (этапе) не только уменьшается объём жидкости в нагнетательной камере (это происходит постепенно), но и её скорость и давление нагнетения возле напорного клапана (резко). Как раз этот механизм и использовался при расчёте нагнетения гидроударом с большими утечками. При правильном расчёте механической сверхъединичности здесь взяться неоткуда (иначе самым сверхъединичным будет «гидроудар со сверхбольшими утечками», то есть простое перемещение жидкости по трубе неизменного или, паче того, расширяющегося сечения — а это явная чушь, не имеющая отношения к реальности).
Причём здесь гравитация?
В качестве источника «лишней» энергии авторы указывают гравитацию. Однако почему-то в теории гравитация никак не фигурирует, а везде используется лишь давление (регулярно попадающееся в формулах ускорение свободного падения служит лишь для перевода давления в традиционный для гидродинамики напор). Единственное условие, для выполнения которого необходима гравитация — это создание давления на рабочей глубине за счёт веса столба воды. Но ведь для того, чтобы создать давление в несколько атмосфер, совсем необязательно погружаться в морскую пучину — можно просто взять насос и достаточно прочную ёмкость... Поэтому позиционирование гидротаранного генератора как «преобразователя гравитационной энергии» совершенно нелогично.
Необоснованная сверхъединичность
Теперь посмотрим на первые формулы, на которых основаны все дальнейшие математические выкладки. Я приведу их в соответствии с нумерацией в статье, лишь заменив некоторые специфические обозначения на общефизические (U → Δv, γ → ρ) и более удобные для записи в текстовом формате (обозначение относительной доли величины ~ → δ).
где H — напор при закачке в воздушный колпак; Δv — часть начальной скорости потока, затраченная на создание этого напора; с — скорость распространения ударной волны; pa — напорное давление среды, окружающей трубу; ρ — удельная плотность воды; g — ускорение свободного падения.
Можно заметить, что в этой формуле «давление» pa измеряется в кг / м2. Однако это не криминал, а следствие традиционного гидродинамического подхода, ориентирующегося не на давление как таковое, а на напор, т.е. высоту статического столба жидкости, находящейся под действием гравитации. Внеся ускорение свободного падения под скобки, можно легко перейти к общефизической записи той же самой закономерности:
(g · H – P / ρ) / с = Δv (1' ),
где давление P уже измеряется, как и положено, в паскалях.
Гораздо интереснее понять, зачем вообще, в отличии от канонической формы формулы Жуковского, сюда введено внешнее давление и что именно имеется в виду под напором H? Судя по всему, это сделано для того, чтобы учесть давление на глубине. Таким образом, H — это именно дополнительный напор выше поверхности, который может обеспечить гидроудар.
Далее в статье вводится ещё несколько базовых формул, основанных, по сути, на давно известной и зарекомендовавшей себя формуле Чистопольского и известных физических закономерностях.
δqН = ζ1 · (1 + φ) · y (2),
где
δqН = qН / (ρ · S0 · L0) (3),
φН = vK / v0 = 1 – 2 · n0 · Δv / v0 (4),
δqH — доля закачанной в колпак воды от её общего количества в нагнетательной камере; qH — масса закачанной в колпак воды; ζ1 — коэффициент, зависящий от φ и n 0, всегда находящийся в диапазоне 0 < ζ1 ≤ 1; ρ — удельная плотность воды; S0 — площадь внутреннего сечения нагнетательной трубы; L0 — длина нагнетательной трубы; v0 — начальная скорость воды; vК — конечная скорость воды в конце закачки; φ — коэффициент соотношения этих скоростей; n0 — число гидравлических ударов на ударный клапан; Δv — часть начальной скорости потока, затраченная на создание нагнетающего напора; у — соотношение эквивалентной начальной скорости и скорости ударной волны; с — скорость распространения ударной волны.
Очевидна коррекция этих формул для нескольких повторных гидроударов введением числа гидроударов n0. Причём характер его введения явно указывает на использование концепции «отражения от вакуума» и неизменной энергии ещё не накачанной воды. Несколько непонятно, причём здесь ударный клапан — ведь по этой концепции он вообще не участвует в повторных гидроударах. Но, скорей всего, это просто опечатка, и в виду имелся всё-таки напорный клапан. Если для единичного гидроудара принять ζ1 = 1 и n0 = 1, как это рекомендуют авторы, то, действительно, формула (2) превращается в давно известную формулу Чистопольского для гидротарана.
Зачем введён коэффициент ζ1? Судя по всему, он призван учесть все потери, в том числе уменьшение нагнетения при повторных гидроударах. Приведена даже его расшифровка, которая, правда, ничего не объясняет, но зато и не используется в дальнейших рассуждениях. К тому же нас предупредили, что изложена лишь часть теории...
Дальнейшие математические выкладки, включая вывод формулы (11) выполнены корректно. Что же мы получили?
H / h = 1 + ζ1 · ((1 – φ2) / δqH) · βy · k0 (11),
где H — напор, созданный гидроударом (относительно уровня напорного клапана); h — внешний напор (глубина размещения установки); βy — коэффициент потерь скорости в ускорительной трубе из-за трения на стенках; k0 — отношение начальной скорости потока к максимально возможной скорости истечения при давлении на глубине размещения нагнетательной трубы; прочие параметры описаны чуть выше. В комментариях к этой формуле авторы утверждают, что в процессе закачки 1 > φ > 0. Как мы выяснили, обсуждая формулу Чистопольского, это не так, более того, для сильных гидроударов с возникновением зоны отрыва неизбежно 0 > φ > –1. Однако в этой и во всех дальнейших формулах φ встречается в только квадрате, и потому на самом деле знак не имеет значения — ведь квадрат вещественного числа не может быть отрицательным. Поэтому, скорее всего, следует читать 1 > φ2 ≥ 0.
Тем не менее, из физического смысла формулы (11) следует однозначный вывод — любой гидроудар сверхъединичен, а одиночный — в особенности (тот самый, что в гидротаране, при ζ1 = 1)! Чем меньше будет доля нагнетённой воды относительно общего объёма нагнетательной камеры δqH, тем выше будет подъём, но и при очень больших объёмах нагнетения, вплоть до 100% (δqH = 1), всё равно будет выполняться условие H > h. Более того, благодаря стоящей отдельно единице оно будет выполняться и в тех случаях, когда нагнетённый объём превышает объём всей воды, участвовавшей в гидроударе, и в 10, и в 100, и в 1000 раз! Кроме того, условие отсечения здесь никак не оговорено, а значит, и любой классический гидравлический таран должен быть сверхъединичным устройством!.. Но ведь в реальности этого нет. И это ещё не всё! Ведь как мы выяснили выше, в формуле (1) H означает именно дополнительный напор. А тогда получается, что любой гидротаран должен поднимать воду над поверхностью на высоту, равную глубине его размещения (из-за «голой» единицы), то есть удваивать энергию первичного гидроудара, плюс ещё маленькая, но всегда положительная добавка, причём такое минимум удвоение энергии должно быть и в мягком резиновом шланге, и в трубопроводах, оснащённых любыми системами компенсации гидроударов! Это уже явно из области ненаучной фантастики. Значит, в расчётах где-то ошибка...
Математические выкладки выполнены безукоризненно, следовательно ошибка таится в физической интерпретации каких-то формул. В самом деле, ведь в формуле (11) величина H интерпретируется авторами как напор от уровня напорного клапана. Но в таком случае и формулу (1) надо было применять в классическом виде — без коррекции, учитывающей давление на глубине, — ведь такой напор уже учитывает глубину! И тогда в формуле (11) у нас сразу исчезает «сверхъединичная» единица, и всё тут же возвращается в жёсткие рамки закона сохранения энергии. А при пристальном рассмотрении формулы (1) становится понятно, что давление на глубине там надо было указывать не с «минусом», а с «плюсом» — ведь гидроудар должен и преодолеть это давление, и создать дополнительный напор (сравните с формулами (1.5) и (1.6))! Тогда и при интерпретации H как дополнительного напора всё становится на свои места — «голая» единица в формуле (11) снова появляется, но уже со знаком «минус», а это делает её полностью эквивалентным результату, полученному на основе классической формы формулы Жуковского — для абсолютного (полного) напора.
Но ведь авторы использовали и ещё один путь расчёта, приведший их к тем же результатам, — через энергии. Значит, там тоже есть ошибка? Есть! Она содержится в формуле (15), где при определении потенциала подъёма воды из напора необосновано вычитается глубина погружения h. Ведь в данном случае H однозначно трактуется как напор гидроудара у напорного клапана, а значит, в этот момент нам нет дела до глубины, на которой находится установка — она уже учтена в E0, — тем более, что вплоть до самой поверхности (в варианте насоса) отводящая ветвь отделена от наружной среды жёсткими стенками воздушного колпака и напорной трубы и никак не подвержена влиянию давления внешней воды! Соответственно, и на этом пути рассуждений тут же появляется ошибочная «сверхъединичная» единица, и последующие формулы вновь утверждают ошибочную мысль о том, что все гидротараны принципиально сверхъединичны с КПД не менее 200%, причём по чисто механическим причинам...
Заключения
Пессимистичное 
Так что же, мы имеем дело с очередным fake-устройством — фальшивкой, «сконструированной» группой аферистов от науки с целью «развода на деньги» богатеньких инвесторов в лучших традициях Остапа Бендера — в белых штанах под пальмами Тенерифе (ибо в наши дни мегаполис Рио-де-Жанейро не слишком комфортен для приятного времяпрепровождения)?
К сожалению, многое говорит за этот вариант. Во-первых, ошибки в теории, незамеченные на бумаге, должны были немедленно проявиться на практике, но ведь «эксперименты прошли успешно». Правда, на представленном в первой статье графике гидроударов повторные множественные гидроудары, длительность которых должна сокращаться, абсолютно не просматриваются. Там присутствуют равномерные гидроудары одинаковой длительности — как в обычном гидротаране. А ведь повторные гидроудары упоминались как один из ключевых моментов, да и при таких измерениях нельзя было не заметить, что ударная волна отражается не от вакуума, а от закрытого клапана... Во-вторых, при чтении статьи под этим углом заметны несколько оговорок-опечаток, намекающих на несколько поверхностное знакомство авторов статьи с этой областью техники. Скажем, говорится, что упомянутая диаграмма давления описывает давление в воздушном колпаке. Но она в принципе не соответствует изменениям давления внутри колпака. Воздух — хороший амортизатор, и он не может дать задний фронт давления, соответствующий выбросу нагнетённой воды под действием сжатого воздуха в колпаке, более резким, чем передний фронт, обусловленный нагнетением воды в колпак под действием гидроудара с давлением в десятки атмосфер. Более, того, в описанном авторами режиме давление в колпаке не может иметь горизонтальных «полочек» — оно должно постепенно нарастать по мере сжатия воздуха нагнетаемой водой, а после закрытия клапана также плавно снижаться по мере вытеснения воды в напорную трубу сжатым воздухом. Показанная же картина изменения давления возможна только тогда, когда практически весь колпак заполнен водой. Но в таком случае по своей функциональности это уже не воздушный колпак, а некая часть напорной трубы...
Есть и другие «проговорки», например, утверждение на с.45 о том, что значение КПД турбины «близко к реальным значениям КПД для таких турбин». Как правило, когда говорят о реально изготовленном и проверенном устройстве, то говорят о «близости к КПД других турбин такого же типа». О «близости к реальным значениям» речь обычно идёт при оценке результатов бумажных или компьютерных расчётов.
О достоверности «экспериментов» в таком случае говорить не имеет смысла. Получать на поверхности нужные результаты «таинственных подводных процессов» в течении не слишком долгого времени при должной изобретательности и подготовке «эксперимента» не так уж трудно.
Надо признать, что если верен этот вариант, то «развод» выполнен на достаточно высоком уровне и весьма элегантно — в экзотической области техники с исторически сложившейся специфической системой расчётов, где очень мало специалистов, которые могут (и имеют желание) найти ошибки в «доказательствах» и опровергнуть ложные выводы!
Оптимистичное 
Но может, авторы генератора честно заблуждаются, а результаты успешно проведённых реальных экспериментов чудесным образом совпали с предсказаниями ошибочной теории? Ошибки же и опечатки в статье объясняются малой компетентностью тех, кто непосредственно готовил статью (хотелось бы думать, что два доктора наук и один кандидат — учёные степени авторов — не допустили бы столь явные ляпы)? Что ж, хоть вероятность таких совпадений невелика, я буду только рад, если пессимистичный вариант окажется неверным!
Тем не менее, из этого не следует, что гидроудар более не представляет никакого интереса.
Ведь гидроудар — на самом деле явление весьма перспективное и не до конца исследованное.
И, конечно, всё вышесказанное никоим образом не компрометирует гидротаран — устройство не только весьма поучительное, но и реально полезное. Летом, до которого уже осталось не очень много, надо будет сделать такой насос. Заодно можно будет и поэкспериментировать с отсекаемой нагнетательной камерой...
Конспирологическое 
А может, все эти повторные гидроудары, схемы и выкладки — лишь сделанная на скорую руку маскировка истинной сути установки, и в самом деле содержащей отбойный клапан, отсекающий нагнетательную камеру, воздушный колпак с напорным клапаном и реактивную турбину, но скомпонованных по-другому? Например, турбина установлена внутри воздушного колпака непосредственно в месте впрыска нагнетаемой струи, и вся энергия, которая в опубликованном варианте расходовалась на бесполезный излишний разгон этой струи в воздушном колпаке, расходуется с пользой на раскрутку турбины, а слишком высокая степень осушения нагнетательной камеры объясняется тем, что за счёт накопленной инерции турбина «высасывает» из неё остаток воды, который не смог подать в воздушный колпак гидроудар? В таком случае можно подобрать объяснение и нелогичной диаграмме давления (скажем, она измерялась на входе турбины, а не в самом пространстве воздушного колпака), и некоторым другим странностям в описании. В частности, повторные гидроудары не имеют решающего значения — вполне можно обойтись и без них, а вот реактивная турбина, применение которой в плотной среде — воде — выглядит, мягко говоря, странным (а это неизбежно при опубликованной схеме), в газовой среде воздушного колпака вполне оправдана. Но тогда задействуются несколько другие принципы работы, возможно, идентичные некоторым из тех, что использовал в своём «домашнем генераторе» и других установках Виктор Шаубергер, а отбойный клапан и гидроудар в нагнетательной камере служат не столько для непосредственного приведения установки в действие, сколько для организации необходимого для её работы прерывистого потока — аналогично атмосферному клапану у Шаубергера. В таком случае гидротаранный генератор работоспособен примерно в той же степени, что и многие конструкции Шаубергера, причём высокое давление на глубине может повысить эффективность и устойчивость работы установки по сравнению с атмосферными условиями...
♦
|