Эффект Котоусова
В «Журнале технической физики» за 2005 год была опубликована статья Леонида Сергеевича Котоусова (Санкт-Петербургский государственный электротехнический университет) «Исследование скорости водяных струй на выходе сопел с различной геометрией» (ЖТФ, том 75, вып.9; с. 8-14, далее в тексте прямые цитаты из этой статьи выделены курсивом). Казалось бы, она посвящена частному вопросу, однако выводы, к которым пришёл автор, отнюдь не частные и имеют прямое отношение к тематике этого сайта. Чтобы убедиться в этом, достаточно прочитать аннотацию: «Обнаружен коэффициент усиления мощности струи до 4 ... 4.5 единиц по отношению к входной мощности потока воды, задаваемой ее входным избыточным давлением и объемным расходом. Рассмотрены причины этого эффекта и источник дополнительной энергии. <...> Газовыделение и кавитация увеличивают этот эффект из-за уменьшения плотности струи. В результате ускорение струи вызывается не только давлением на входе, но и снижением потенциальной энергии текущей среды за счет снижения ее абсолютного давления вплоть до уровня технического вакуума. Обжатие струи воздухом атмосферы и восстановление равновесного с воздухом давления в воде приводят в итоге к повышению кинетической энергии струи за счет внутренней энергии воздуха.»
Отсюда следует, что исследованный Котоусовым эффект может не только объяснить механизм работы различных гидродинамических конструкций (Шаубергера, Клема, Шерью и др.), но и имеет огромную практическую ценность сам по себе. Подробности можно найти в оригинальной статье, которая написана простым и понятным языком (математические выкладки с роторами и градиентами вполне можно пропустить — они лишь подтверждают то, что сказано в тексте). Здесь же я хочу популярно изложить наиболее важные моменты и обсудить их с точки зрения возможности практического получения «энергии из воздуха».
Особо следует подчеркнуть, что Котоусов — известный и уважаемый учёный, автор одного из учебников термодинамики, излагающего эту науку с вполне традиционных позиций. Так что он отлично понимал все последствия публикации этой статьи, и вряд ли стал бы публиковать её без многократной проверки и твёрдой уверенности в истинности полученных экспериментальных результатов.
Update 2011. Не всё так однозначно с описанным эффектом. Первая независимая попытка воспроизвести этот эффект не показала превышения силы струи над рассчитанной по классической методике. После на первый взгляд незначительного изменения геометрии сопла эффект проявился, и его можно считать получившим независимое подтверждение, однако некоторые закономерности существенно отличались от наблюдаемых Котоусовым. Так что требуются дальнейшие исследования этого эффекта.
Традиционная гидродинамика об истечении струй
Изменение характера свободной струи по её длине
Эффект сужения (сжатия) истекающей струи
Несовершенное сжатие истекающей струи
Истечение под уровень
Истечение через насадок
Давление струи на преграду
Инверсия струй
Опыты и выводы Л.С.Котоусова
Предмет изучения
Особенности опытов
Результаты опытов
Основные результаты опытов, отмеченные Л.С.Котоусовым
Другие замечания и наблюдения Л.С.Котоусова
Особенности эффекта в свободной воздушной струе
Анализ причин, обуславливающих обнаруженный эффект
Объяснение причин возникновения эффекта Котоусова
Котоусов об энергетическом балансе в обнаруженном эффекте
Почему эффект Котоусова не был обнаружен раньше?
Ограничения и использование эффекта Котоусова
Е.И.Андреев об эффекте Котоусова
О размерах и форме сопла
Размер имеет значение
Лучше меньше, да лучше?
Об оптимальной форме сечения струи
О продольном профиле сопла
О нагнетающем давлении
Об эффекте Котоусова в лотках и при разгоне воды без использования сопел
О влиянии закручивания струи
Оценка мощности струи под давлением
Об импульсном режиме струи и гидроударах
Традиционная гидродинамика об истечении струй
Нельзя сказать, что до Котоусова истечение струи из сопла никто не исследовал. Наоборот, исследованиями в этой области знаменитый Николай Егорович Жуковский занимался ещё на рубеже XIX-XX веков. В традиционной гидродинамике этой теме уделено немалое внимание. Как правило, она выделяется в отдельный раздел под названием вроде «Истечение жидкости из отверстий, насадков и из-под затворов». Прежде чем переходить непосредственно к опытам Котоусова, посмотрим, о чём же там говорится.
Изменение характера свободной струи по её длине
Нетрудно убедиться, что струя, вытекающая под давлением в атмосферу и не ограниченная какими-либо стенками (так называемая «свободная струя») возле отверстия, из которого она вытекает, является практически монолитной, а затем постепенно превращается в поток отдельных капель.
В гидродинамике выделяют 3 стадии развития свободной струи.
-
Компактная (монолитная) стадия начинается возле отверстия, через которое истекает жидкость, и продолжается на некотором расстоянии от него. Обычно это расстояние составляет от нескольких сантиметров до метра с небольшим и зависит от множества условий, среди которых не только скорость истечения и вызвавший её перепад давлений, но и вязкость жидкости, сила её поверхностного натяжения, а также сопротивление внешней среды (воздуха). На протяжении компактной части струя сохраняет свой средний диаметр практически неизменным.
-
Раздробленная стадия характеризуется началом разделения струи на отдельные очень мелкие капли, однако они не разлетаются далеко, а продолжают «сопровождать» ядро струи. При этом значительная часть струи остаётся компактной и сохраняет монолитность, но по мере удаления от начала струи кажется, что ядро струи слегка сужается. Длина раздробленной части обычно примерно равна или несколько меньше длины компактной части струи.
-
На распылённой (капельной) стадии струя уже представляет собой расширяющийся поток отдельно летящих капель — в центре более крупных, по краям более мелких. Постепенно под действием воздуха крупные капли дробятся до тех пор, пока силы поверхностного натяжения не смогут компенсировать разрывающее воздействие скоростного напора воздуха.
В свободной струе, истекающей в жидкость (в так называемой «затопленной струе») образования отдельных капель, естественно, не происходит. Вместо этого возникают турбулентные возмущения на границе между струёй и окружающей жидкостью — сначала небольшие, а затем захватывающее всё сечение струи и постепенно рассеивающие её кинетическую энергию.
Как правило, наибольший интерес представляет компактная (монолитная) часть струи. Именно она определяет скорость истечения и, соответственно, расход жидкости, и именно к ней относится всё изложенное ниже. Расчёт прочих частей струи слишком затруднён в силу необходимости учёта большого числа дополнительных факторов и внешних условий (вплоть до силы ветра и влажности наружного воздуха), но на сам процесс истечения из резервуара или трубы их влияние весьма мало.
Эффект сужения (сжатия) истекающей струи
Этот эффект заключается в том, что сечение струи, истекающей под давлением через отверстие с пренебрежимо малой длиной канала (в тонкой стенке или с острыми кромками с обратной конусностью) после прохождения самого отверстия диаметром dO продолжает уменьшаться, пока не достигнет диаметра сжатия dC, который заметно меньше диаметра просвета отверстия.
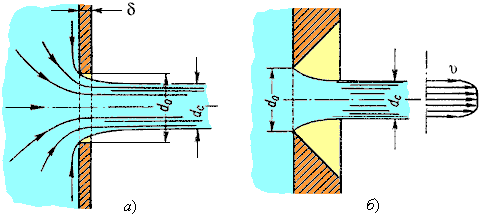 Эффект сужения истекающей струи (по материалам сайта http://gidravl.narod.ru/):
а) истечение через отверстие в тонкой стенке толщиной δ; б) истечение через раззенкованное отверстие (кромки с обратной конусностью). dO — диаметр отверстия; dC — диаметр сжатой струи. Справа показано распределение скоростей v по сечению струи.
Степень сжатия струи ε характеризует соотношение площадей сечения сжатой струи SC и отверстия SO:
ε = SC / SO = (dC / dO)2 ≤ 1 (1.1).
Эффект видимого сжатия объясняется движением жидкости с различных направлений, в том числе и радиального (относительно струи) движения по стенке, к осевому движению в струе. Однако при этом считается, что давление в струе после отверстия равно давлению внешней среды или близко к нему, то есть чаще всего это обычное атмосферное давление. В связи с этим не предполагаются сколь-нибудь значительные кавитационные явления, и, поскольку жидкости в первом приближении можно считать несжимаемыми, то в данной традиционной трактовке правильнее говорить не о сжатии струи, а о её сужении. При этом в соответствии с законом непрерывности струи по мере сужения сечения пропорционально должна возрастать скорость струи, т.е. скорость жидкости в момент прохождения отверстия заметно меньше, чем на некотором расстоянии от него. Тем не менее в дальнейшем для предотвращения путаницы терминологии я всё же буду использовать устоявшийся термин «сжатие струи», тем более что неизбежное при сужении ускорение струи в традиционной гидродинамике как-то обходится молчанием.
Чтобы оценить порядок реальной степени сжатия, можно воспользоваться данными, приводимыми Л.С.Котоусовым: при диаметре отверстия dO = 4.6 мм диаметр сжатой струи составлял от 3.6 мм при небольших входных давлениях (< 1 атм) до 3.8 мм при повышенных (> 3 атм). Таким образом, степень сжатия, равная отношению квадратов диаметров, составляла от 61% до 68%.
Несовершенное сжатие истекающей струи
Если размеры резервуара возле места истечения ограничены (например, жидкость к отверстию подаётся по достаточно узкой трубе), то стенки резервуара оказывают влияние на формирование истекающей струи. В этом случае имеет место несовершенное сжатие, которое проявляется как увеличение минимального («сжатого») диаметра истекающей струи. Объясняется это тем, что радиальное относительно оси струи движение жидкости вдоль стенки с отверстием, являющееся причиной сужения струи, в силу ограниченного размера не развивается так сильно, как в резервуаре больших размеров.
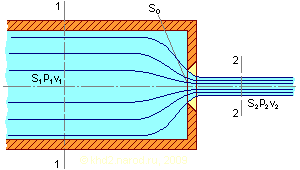 Несовершенное сжатие истекающей струи. SO — площадь отверстия; Si, Pi, vi — сечение, давление и скорость потока на различных участках.
Очевидно, что режимы «совершенного» и «несовершенного» сжатия определяются не только геометрическими размерами резервуара, но и скоростью истечения жидкости (вызывающей её разностью давлений внутри и снаружи резервуара). Чем больше скорость в резервуаре, тем большее влияние оказывают его стенки, ограничивающее сечение потока. Именно этим эффектом объясняется вышеупомянутое увеличение диаметра сжатой струи по мере роста давления и скорости истечения, наблюдавшееся Л.С.Котоусовым.
Степень несовершенного сжатия принято оценивать по эмпирической формуле Н.Е.Жуковского:
ε = 0.57 + 0.043 / (1.1 – S0 / S1) (1.2),
где ε — степень сжатия струи; S1 — площадь сечения резервуара в направлении движения жидкости к отверстию; SO — площадь сечения отверстия.
Кстати, из этой формулы следует, что для «бесконечно большого резервуара» (S0 / S1 → 0) степень сжатия струи равна 60.9%, что отлично согласуется с полученным Л.С.Котоусовым значением 61% для малых избыточных давлений, когда скорости невелики и влияние продольных стенок подающей трубы незначительно.
А теперь вопрос, который закономерно следует из базовых принципов гидравлики. Из соотношения площадей сжатого сечения струи к сечению отверстия в 61% по закону непрерывности потока следует то, что скорость в сжатом сечении более чем в 1.6 раза выше, чем в створе отверстия, а кинетическая энергия струи соответственно больше почти в 2.7 раза! Откуда берётся такая прибавка энергии струи уже после прохождения отверстия, если, по традиционным представлениям, в отверстии поток является монолитным и его плотность практически равна плотности неподвижной жидкости, особенно при малых скоростях истечения, когда вроде бы нет никаких условий для возникновения кавитации, но эффект сжатия струи как раз наиболее силён? Возможно, решение полагается очевидным — в момент прохождения отверстия жидкость имеет существенную радиальную компоненту скорости, не отражаемую в её продольном перемещении, определяемом законом непрерывности, а затем по мере сжатия струи эта компонента «разворачивается» и добавляется к исходной продольной скорости потока, увеличивая её. Но тогда почему при рассмотрении сжатия струи этот важнейший момент не освещается подробно?
Но пока продолжим знакомиться с традиционными представлениями.
Истечение под уровень
В случае, когда струя истекает не в атмосферу, а в среду той же жидкости, в гидродинамике принято говорить об «истечении из затопленного отверстия» или «истечении под уровень». При этом необходимым условием такого истечения является превышение давления внутри резервуара над давлением жидкости вне его. Обычно эта разность давлений либо создаётся непосредственно с помощью насоса, либо её можно получить, обеспечив разные уровни жидкости в резервуаре и вне его.
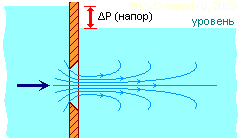 Истечение под уровень. Красной стрелкой отмечен перепад уровней, для которого следует рассчитывать разность давлений (напор) независимо от глубины размещения отверстия.
Традиционная гидродинамика утверждает, что здесь имеют место те же самые закономерности, что и при истечении в атмосферу, в том числе и сжатие струи, так что все вышеприведённые формулы сохраняют свою силу. Единственный нюанс заключается в том, что в качестве разности давлений (или напора) следует принимать соответствующую величину на уровне свободной поверхности жидкости, в которую истекает струя, и если напор создаётся разностью уровней, то его величина не зависит от изменения глубины отверстия истечения, пока оно не приблизится к поверхности. Это связано с тем, что при изменении глубины столбы жидкости с обоих сторон отверстия изменяются одинаково, а значит, разность давлений, вызывающая движение жидкости, остаётся постоянной.
Следует заметить, что для струй, истекающих в непосредственной близости от границы раздела сред, когда струя оказывает заметное влияние на профиль поверхности жидкости (полупогружённых, очень близко над поверхностью или с очень малой глубиной погружения), расчёт несколько усложняется, а коэффициенты могут меняться, однако общие принципы остаются теми же самыми.
Истечение через насадок
На практике очень часто жидкости вытекают через отверстия, продольный размер которых сравним с их диаметром или превышает его. Это необязательно должен быть специально приваренный патрубок, — простое отверстие небольшого диаметра в достаточно толстой стенке оказывает на струю аналогичное влияние. В таких случаях уже нельзя пренебречь влиянием внутренней поверхности отверстия на протекающую по нему струю. Подобный относительно короткий канал, влияющий на форму протекающей по нему струи, но в то же время имеющий достаточно малое собственное гидродинамическое сопротивление, в гидродинамике называется «насадок». Простейшим случаем является насадок с цилиндрической внутренней поверхностью.
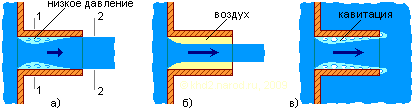 Истечение через цилиндрический насадок. a) в атмосферу (и в жидкость) с малой скоростью; б) в атмосферу с большой скоростью; в) в жидкость (под уровень) с большой скоростью; 1-1 — сечение, соответствующее наибольшему сжатию струи; 2-2 — сечение струи на выходе из насадка.
Также, как и при истечении из отверстия в тонкой стенке, в начале насадка струя испытывает сжатие из-за радиальной компоненты скорости вытекающей в отверстие жидкости. При этом у стенок насадка образуется область пониженного давления. Однако затем по мере продвижения струя под действием этого пониженного давления расширяется, заполняя всё внутреннее сечение насадка, и давление выравнивается. C помощью уравнения Бернулли можно оценить падение давления в сечении 1-1, соответствующем месту наибольшего сжатия струи:
P1 ~ P2 – 0.75 · P0 = P2 – 0.75 · H · g · ρ (1.3),
где P1 — наименьшее давление внутри насадка; P0 — давление внутри резервуара; P2 — давление снаружи насадка в сечении 2-2 (внешнее давление); H — напор (высота столба жидкости); g — ускорение свободного падения; ρ — плотность жидкости в резервуаре.
Очевидно, что при повышении давления в резервуаре P0 пониженное давление P1 довольно быстро может стать отрицательным, т.е. ниже давления вакуума. Поскольку такое состояние физически невозможно, то в этот момент происходит изменение режима истечения жидкости — он прекращает быть безотрывным и отрывается от внутренних стенок насадка на всём протяжении его длины. При этом в образовавшуюся щель поступает наружный воздух, заполняющий область между струёй и внутренними стенками насадка (хотя вследствие эжекции воздуха струёй давление там всё равно будет ниже, чем в свободном пространстве у выхода насадка). Из формулы (1.3) следует, что вызывающее подобную смену режимов течения критическое давление P0 кр можно вычислить по формуле
P0 кр ~ 4 · P2 / 3 (1.4).
Характерно, что в этой формуле не фигурируют параметры самого насадка — ни его длина, ни его диаметр. Поскольку стенки насадка в режиме истечения с отрывом уже не оказывают заметного влияния на характер струи, считается, что в этом случае действуют те же закономерности, что и при свободном истечении через отверстие в тонкой стенке.
Если условия для возникновения режима отрыва от стенок появляются при истечении струи через затопленный насадок, область разрежения, конечно, не заполняется воздухом. Вместо этого там возникают кавитационные явления. То же самое может происходить и в случае истечения через слишком длинный насадок (трубу).
Давление струи на преграду
При столкновении с преградой струя оказывает на неё давление с силой, определяемой в первую очередь расходом жидкости и её скоростью, но также зависящей от формы преграды и угла столкновения.
F = k · Q · v · ρ = k · S · v2 · ρ (1.5),
где F — сила давления струи на преграду; k — безразмерный коэффициент, зависящий от формы преграды и условий столкновения (коэффициент формы); Q — объёмный расход жидкости, м3 / с; v — скорость струи; ρ — плотность жидкости в струе; S — площадь поперечного сечения струи (если сечения преграды меньше сечения струи, то следует брать площадь сечения преграды).
В частности, коэффициенты формы для наиболее часто встречающихся случаев неподвижных преград приведены в таблице.
| Тип преграды |
Коэффициент формы |
Примечания |
Перпендикулярная плоскость
 |
k = 1 |
Жидкость растекается по плоскости, а не отражается от неё. |
Небольшая узкая преграда
 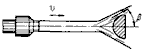 |
k = 1 – cos(β) < 1 |
Сила давления определяется внутренним углом разлёта жидкости β, измеренным на кромке преграды. |
Отражение с частичным разворотом струи
 |
k = 1 + cos(β) > 1 |
Сила давления определяется углом разворота струи β, измеренным на кромке преграды. |
Отражение с полным разворотом
  |
k = 2 |
Характер разворота не влияет на давление при условии, что струя не тормозится. |
Плоскость под углом
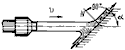 |
k = sin(α) ≤ 1 |
Сила давления определяется углом α между плоскостью преграды и осью струи. |
Очевидно, что указанные в таблице коэффициенты формы аналогичны коэффициенту передачи импульса для абсолютно упругого механического столкновения твёрдого тела с преградой при соответствующем угле отскока. В случае, если струя содержит пузырьки газа или к моменту столкновения с преградой уже переходит в раздробленную либо распылённую стадии, в качестве плотности следует брать усреднённую плотность по всему сечению струи возле преграды.
Инверсия струй
Наконец, в курсе гидродинамики иногда упоминается о явлении инверсии струи, свободно истекающей в атмосферу, которое заключается в изменении формы её сечения по мере удаления от отверстия. Наиболее заметно это проявляется для небольших (до нескольких сантиметров) некруглых отверстий. В качестве основного объяснения предлагается действие сил поверхностного натяжения на вытекающие криволинейные струйки и влияние различных условий сжатия по периметру отверстия.
Силами поверхностного натяжения можно объяснить и хорошо видимое «набухание» внешних кромок такой струи, возникающее уже на достаточно близком расстоянии от места истечения. Возможно, с их помощью также можно объяснить периодическое изменение характера инверсии по длине струи, которое иногда выглядит как спиральное закручивание истекающей струи, мало зависящее от поперечной закрутки потока жидкости на срезе отверстия. Такое изменение характера особенно хорошо заметно для плоских струй с сечением около сантиметра при не слишком больших скоростях истечения, когда на компактную (монолитную) часть струи приходится несколько периодов таких изменений. Иногда это действительно спираль, а иногда лишь похоже на неё.
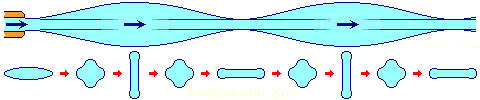 Периодическое изменение инверсии струи. Вверху — идеализированный псевдоспиральный вид струи с периодической инверсией, истекающей из узкого овального отверстия, внизу — сечения этой струи на разных расстояниях от отверстия.
Обратите внимание, что показанное лишь внешне похоже на спиральное закручивание. Впрочем, вряд ли хоть в какой-то книге по гидродинамике Вы что-нибудь найдёте об этом важном, на мой взгляд, явлении. Но зато в этом легко убедиться воочию — достаточно при открывании пакета с молоком или соком сделать срез в виде недлинной и узкой щели, — и изучайте инверсию струи до тех пор, пока пакет не опустеет! При этом в зависимости от формы и размеров отверстия, а также условий подачи жидкости к нему, можно наблюдать и спиральные, и различные псевдоспиральные формы струи — простор для исследований огромный. Следует заметить, что по мере удаления от отверстия псевдоспиральная инверсия стремится превратиться в истинно спиральное закручивание струи, если, конечно, к этому моменту струя ещё не становится распылённой.
Опыты и выводы Л.С.Котоусова
Теперь, получив общее представление о традиционном описании истечения струй, можно переходить непосредственно к опытам, проведённым Л.С.Котоусовым.
Предмет изучения
Что же изучал Котоусов в этих опытах? Он изучал истечение струй в атмосферу из сопел различной формы и относительно небольшого сечения (от 10 мм2 до 5 см2) при достаточно высоких избыточных давлениях (до 0.6 МПа, т.е. ~6 атм). Всего «было исследовано более ста различных сопел: круглых и прямоугольных по сечению, прямых и кривых, с гладкими и ступенчатыми внутренними стенками, с круговым, овальным и кольцевым выходными каналами». Судя по статье, основная масса экспериментов выполнялась с соплами, срез которых имел круглое сечение диаметром 4.5 .. 5 мм (площадь сечения 16 .. 20 мм2) при избыточных давлениях от 5·103 до 3.5·105 Па (~0.05 .. 3.5 атм), а опыты с другими параметрами сопел носили скорее не систематический, а контрольный характер. Однако открытый эффект подтвердился во всех опытах — как в основной серии, так и в контрольных.
В ходе опытов Л.С.Котоусов сравнивал отношение кинетической энергии струи к потенциальной энергии воды на входе сопла. Это соотношение, обозначенное Котоусовым буквой q, вычислялось по следующей формуле (здесь и далее оригинальные буквенные обозначения величин из статьи заменены мною на общефизические):
q = ρ · v2 / (2 · P) = m' · v2 / (2 · P · Q) (2.1),
где q — отношение кинетической энергии струи к потенциальной энергии воды на входе в сопло; ρ — плотность воды на входе в сопло; v — средняя скорость струи в месте измерения; P — избыточное (относительно атмосферы) давление на входе в сопло; m' — массовый расход воды, кг / с; Q — объёмный расход воды, м3 / с.
Котоусов отмечает: «величину q можно трактовать как коэффициент преобразования энергии или мощности потока среды с помощью сопла. Он также имеет смысл относительного динамического (скоростного) напора струи, в который формально входит не плотность среды в струе, а ее плотность на входе в сопло». Я бы предложил для этой величины более короткое название — «коэффициент энергетической эффективности сопла».
В статье специально подчёркивается, что «все исследованные сопла были изготовлены так, что их входные сечения в 10—20 раз превышали сечения среза. Поэтому статическое входное давление отличалось от полного давления не более чем на 1%. Статическое давление измеряли с помощью образцового манометра, а при малых входных напорах для контроля использовали водный манометр». Такой подход исключает объяснение открытого эффекта как следствия погрешностей самой методики измерения давления, вызванных пренебрежением эффектом Бернулли при определении потенциальной энергии воды на входе сопла.
Особенности опытов
Важнейшим условием опытов было непосредственное измерение скорости струи (микротурбиной) или её скоростного напора (пружинным динамометром специальной конструкции) в отличии от обычно используемой в гидродинамике косвенной оценки скорости, которая рассчитывается на основе измерений расхода и сечения струи. Стробоскопический метод измерения скорости вращения микротурбины и тарировка динамометра обеспечивали достаточно высокую точность измерений, — по оценке самого Котоусова, «максимальный разброс данных в пределах 10%, а доверительный интервал для случайной погрешности измерения средней скорости струи v в пределах 5%», — это в десятки раз меньше величины обнаруженного эффекта.
Лопасть динамометра была выполнена таким образом, чтобы обеспечить разлёт воды в плоскости, перпендикулярной оси струи, что соответствует коэффициенту формы преграды k = 1. Поэтому при определении скорости струи по давлению на измерительную лопасть динамометра использовалась формула
где v — средняя скорость струи в месте измерения; F — сила давления струи; m' — массовый расход воды, кг / с; 1.4 — коэффициент, учитывающий «частично неупругое взаимодействие струи с лопастью», найденный «путем сравнения результатов измерения скорости с помощью динамометра и микротурбины» при малых давлениях на входе сопла и экстраполированный на весь диапазон давлений, использованных в ходе экспериментов, причём автор отмечает, что это несколько заниженное и потому наиболее невыгодное для обнаруженного эффекта значение. Со своей стороны, хочу заметить, что этот коэффициент численно равен √2; возможно, это просто совпадение...
Массовый расход легко и с высокой точностью определялся сбором сливающейся воды в мерную ёмкость и измерением времени накопления при условии достаточно постоянного напора (по описанной методике изменение давления за время эксперимента составляло не более нескольких долей процента).
От себя замечу, что все эти формулы и ход рассуждений не вызывают нареканий с точки зрения классической механики, и потому ошибок, подобных допущенным в опубликованной теории гидротаранного генератора, я здесь не вижу. Точность измерений также достаточно высока. Так что обнаруженный эффект трудно списать на неверную методику или на измерения внутри пределов погрешности.
Наконец, ещё несколько цифр, касающихся этих опытов. Котоусов пишет, что для сопел диаметром не более 5 мм сжатое сечение находилось на расстоянии от 1.5 до 3 мм от среза сопла, далее следовала компактная (монолитная) часть струи длиной 50 .. 70 см, а её распылённая (капельная) часть обычно начиналась на расстоянии порядка 1.2 м от среза сопла.
Результаты опытов
Главный и наиболее сенсационный результат этих опытов — измеренная скорость соответствует кинетической энергии струи, до 4.5 раз превышающей её потенциальную энергию, обусловленную гидравлическим давлением у входного сечения сопла! Как уже говорилось выше, столь большое превышение нельзя списать на погрешности измерений. Даже повышающий коэффициент в формуле (2.2), будучи возведённым в квадрат, может дать лишь двукратное превышение, а без такого коэффициента эта формула соответствует заведомо нереальному абсолютно упругому взаимодействию воды с лопастью динамометра. Но даже без этого коэффициента (который, на мой взгляд, введён совершенно корректно), превышение будет более чем двукратным!
На рисунке показаны результаты измерений коэффициента энергетической эффективности сопла q для различных продольных профилей круглых сопел.
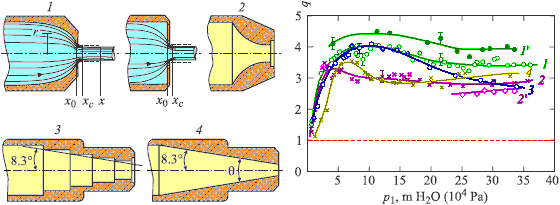 Результаты измерений q для различных профилей сопла одинакового диаметра. Номер линии на графике справа соответствует номеру сопла слева (удаление 5 .. 50 см от среза сопла, линии, обозначенные цифрами со штрихом, соответствуют измерениям на расстоянии 70 .. 120 см). Ярко-красной линией показано предельное соотношение для идеальной жидкости без потерь; по общепринятым представлениям для реальных жидкостей вследствие потерь q всегда должно быть ниже этой линии.
Следует сказать несколько слов об особенностях показанных профилей сопла.
-
С возрастающей к выходу кривизной профиля. По результатам непосредственного измерения Котоусовым статического давления по длине и радиусу сопел и в струе, качественный вид линий тока в нём аналогичен отверстию в тонкой стенке, траектория струек имеет параболическую форму (показано справа от сопла №1).
-
Короткое коноидальное. С традиционной точки зрения, обеспечивает наибольший расход жидкости (а следовательно, и скорость) по сравнению с другими профилями при прочих равных условиях.
-
Ступенчатое. Средний по длине угол раствора конуса такой же, как и у гладкого конического сопла №4. С традиционной точки зрения, ещё более ухудшить условия истечения струи и получить большее гидравлическое сопротивление сопла, не уменьшая явно его просвет, можно, пожалуй, лишь создавая противоток жидкости внутри сопла.
-
Гладкое коническое. С традиционной точки зрения, имеет оптимальный внутренний профиль для обеспечения максимальной кинетической энергии струи на больших дистанциях. Поэтому именно так обычно изготавливают наконечники шлангов, пожарных брандспойтов, гидромониторов и прочих устройств, где необходимо получить максимальную силу и дальность струи.
Во избежание путаницы и ложных выводов ещё раз хочу напомнить, что на этом графике отображено именно соотношение кинетической и потенциальной энергий струи, а не её абсолютная кинетическая энергия, которая с ростом давления возрастает монотонно. Это видно по взятому из той же статьи графику зависимости скорости струи от давления на входе для сопла №2 (сиреневая линия на предыдущем графике) — здесь характерный «горб» в диапазоне 0 .. 5·104 Па совершенно отсутствует.
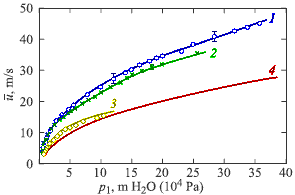 Результаты измерений зависимости скорости струи от давления для сопла №2. 1 (синяя) — измерения методом динамометра на расстоянии 5 .. 50 см от среза сопла; 2 (зелёная) — измерения методом микротурбины в 10 см от среза сопла; 3 (жёлтая) — по среднему диаметру струи в сжатом сечении и расходу воды (традиционный гидродинамический подход); 4 (красная) — по уравнению Бернулли в одномерном представлении для идеальной воды (без потерь); по общепринятым представлениям для реальных жидкостей вследствие потерь все скорости должны быть ниже красной линии.
Для других типов сопел характер и взаиморасположение линий аналогичны.
Особо подчеркну, что приведённые результаты для большей части диапазона получены двумя независимыми друг от друга методами (динамометр и микротурбина), которые достаточно хорошо совпадают друг с другом. При очень высоких скоростях струи (более 30 м/с) микротурбина, похоже, не использовалась из-за слишком высоких динамических требований, однако часть графика, где применялись оба метода, убеждает в том, что динамометрические измерения вполне корректны.
Ещё один очень важный факт: результаты измерения скорости струи (линия 3), полученные общепринятым в гидродинамике «интегральным» методом (по расходу и видимому диаметру) намного меньше результатов непосредственных измерений и очень близки к результатам традиционного расчёта (линия 4), так что имеющееся небольшое превышение легко списать на погрешности измерений. Видимо, это одна из причин, по которым замеченный Котоусовым эффект ранее не был обнаружен и исследован как самостоятельное явление.
. . .
Здесь приведены лишь наиболее значимые, на мой взгляд, иллюстрации. Для того, чтобы ознакомиться со всеми результатами опытов и подробной методикой их проведения, следует обратиться к оригинальной статье.
Основные результаты опытов, отмеченные Л.С.Котоусовым
Вот какие результаты и обнаруженные закономерности (некоторые из которых, мягко говоря, парадоксальны и противоречат традиционным представлениям) наиболее важными считает сам автор.
-
Установлено, что для сопел, представленных на рисунке, при температуре воды от 8 до 40°C величина q практически не зависит от температуры воды.
-
В опытах, результаты которых представлены на рисунках, температура воды была в интервале 8–10°C. Установка лопасти динамометра производилась на расстояниях 5 .. 150 см от среза сопла. Отдельные измерения делали и на расстояниях до 3 м по горизонтали. Скорость струй постоянна в пределах погрешности до расстояния 50 см для всех сопел, слегка возрастает на практически еще горизонтальном участке траектории (при повышенных входных давлениях) до 1.2 м для сопел №1 и №3 и слегка убывает для сопел №2 и №4. Далее для всех сопел и горизонтальная составляющая, и полный напор убывают.
-
Относительный скоростной напор q имеет размытый максимум на уровне 3.3 .. 4.5 в области входных давлений 5–15·104 Па (0.5–1.5 атм) для разных сопел, далее он немного спадает и равен 2.5 .. 4.
-
По форме профиля сопло №1 имеет большее гидравлическое сопротивление, чем сопло №2, но оно оказывается энергетически более эффективным. Аналогично сопло №3 должно иметь большее сопротивление, чем гладкое сопло №4 с тем же средним углом наклона образующей профиля к оси сопла. Тем не менее сопло №3 лучше.
-
Определение скорости струй путем измерения их диаметра и расхода воды допустимо с погрешностью не более 20% лишь при входных давлениях ниже 3·104 Па (0.3 атм).
-
Приводимый в различных руководствах по гидравлике <...> коэффициент потерь напора струи жидкости величиной 0.92 .. 0.96 при взаимодействии с нормально установленной преградой без ссылки на экспериментальные данные представляется нам сомнительным. Еще более неправдоподобно предположение о равенстве скоростей струй, набегающих на лопасть и покидающих ее, при рассмотрении динамических свойств струи. Исследование этих скоростей с помощью предложенной методики с динамометром позволило установить, что отлетающие от лопасти струи имеют скорость в среднем в 1.5 раза ниже, чем набегающая струя. Это также согласуется с поправочным коэффициентом в формуле (2.2).
Другие замечания и наблюдения Л.С.Котоусова
Здесь я хочу отметить те разбросанные по тексту статьи факты, которые автор не счёл нужным отнести к наиболее важным результатам. Тем не менее, на мой взгляд, они имеют очень существенное значение для понимания происходящих процессов и для попыток использования их в реальных технических устройствах.
О геометрических параметрах сопла: «...было также найдено, что круглые конические сопла наиболее эффективны, если их длина приблизительно равна входному диаметру. Отметим еще, что при прочих равных условиях кривые сопла могут быть эффективнее прямых».
О захвате струёй прилегающего воздуха: «Трение струи о воздух и эжекция воздуха струей влияют на измерение ее скорости. В данном эксперименте при прочих равных условиях сила F оставалась постоянной при увеличении диаметра лопасти более 3 см. При снижении его до 2.2 и 1.3 см величина F снижалась соответственно на 5–6 и 10–12%». Это говорит о том, что существенная доля кинетической энергии приходится на окружающий струю воздух, вовлечённый ею в движение. При этом плотности воды и воздуха различаются примерно в 800 раз, так что для того, чтобы поток воздуха, движущийся со скоростью струи воды, нёс 10% общего кинетического импульса, его диаметр должен быть приблизительно в 9 раз больше диаметра этой струи. Примерно это мы и видим (3.5 .. 4 мм у струи в сжатом сечении и 3 см общий диаметр, включая воздух).
О минимальной длине струи: «При установке лопасти динамометра на расстоянии от 5 до 40 см от среза для этой группы сопел получаем практически постоянные величины F. Приближение лопасти к срезу до расстояния в 1 см давало постепенное снижение F на 20–30%». Это серьёзное указание на то, что значительную часть кинетической энергии струя приобретает именно на открытом участке в воздухе после среза сопла. К сожалению, график этой зависимости в статье отсутствует, нет и сведений об измерениях на более близкой дистанции — вероятно из-за того, что очень близкая преграда уже слишком сильно влияет на само истечение струи из сопла.
Особенности эффекта в свободной воздушной струе
Является ли обнаруженный Л.С.Котоусовым эффект специфическим именно для истекания жидкости в воздух? Нет, не является. В конце статьи автор говорит следующее: «Проведены аналогичные исследования с воздухом вместо воды, и для измерения скорости потока и струи применили трубку Пито. Для воздуха также коэффициент преобразования мощности потока q больше 1 и может достичь более чем 1.3 вблизи критических параметров течения и в сверхзвуковом потоке. Однако этот коэффициент существенно ниже, чем у воды».
Очевидно, этот эффект является универсальным, однако степень его проявления определяется параметрами вещества струи и внешней среды, прежде всего их сжимаемостью и плотностью. В частности, при истечении в воздух воздушной же струи, вещество струи благодаря высокой скорости свободного теплового движения частиц (ведь это газ!) тотчас же стремится заполнить возникающие области пониженного давления, в результате чего большого разрежения и, следовательно, разности давлений, необходимой для видимого проявления эффекта, удаётся достичь лишь при очень больших скоростях потока, когда скорости теплового движения частиц уже не хватает для эффективного заполнения возникающих «пустых» областей. Однако при этом и окружающий воздух по той же самой причине уже не успевает обжимать струю с достаточной силой, — этим можно объяснить относительно невысокий коэффициент энергетической эффективности такой струи.
Анализ причин, обуславливающих обнаруженный эффект
Убедившись в том, что эффект вполне реален, устойчиво воспроизводится и не может быть объяснён ошибками методики или погрешностями измерений, Л.С.Котоусов, естественно, задумался о причинах, его вызывающих, а заодно и о том, почему он не был обнаружен раньше. Здесь я лишь изложу приводимое им качественное описание причин эффекта, а желающим посмотреть математическое обоснование придётся обратиться непосредственно к оригинальной статье, и без знания высшей математики там не обойтись.
Объяснение причин возникновения эффекта Котоусова
Котоусов отмечает, что традиционно в гидродинамике используется линейный вариант уравнения Бернулли — по току жидкости вдоль центральной оси трубы. «В действительности происходит уменьшение абсолютного статического давления в потоке внутри сопла и в струе вблизи среза сопла до уровня ниже атмосферного вследствие поворота течения и векторов ускорения и скорости элементарных струек в основном объеме среды, за исключением непосредственно приосевой части. Следовательно, в трубах переменного сечения и в соплах необходимо учитывать радиальную составляющую градиента статического давления, которая иногда может даже превышать осевую составляющую (здесь также заметим, что трение потока о стенку и увеличение кривизны образующей профиля сопла к его срезу также будут повышать указанную радиальную составляющую)».
Вид траекторий струек в случае отверстия в тонкой стенке показан выше на рисунке с разрезом сопла №1. «Форма струи непосредственно наблюдаема. Вид траекторий элементарных струек внутри сопла соответствует нашим данным по измерению статического давления в радиальном и продольном направлениях с помощью миниатюрных датчиков из тонкостенных капилляров диаметром 0.8 мм. Применяли и статическую, и подвижную в обоих направлениях установки датчиков как внутри сопла, так и вне его. Измерения в струе возможны только при введении капилляра вдоль струи со стороны сопла. Наряду с этим непосредственно измеряли давление над струей вблизи среза, окружив ее камерой, как в водоструйном насосе, и вводя в стенку камеры обычный датчик статического давления. В данной статье опущены подробности этих измерений. Здесь существенно, что отрицательное избыточное давление может наблюдаться не только в струе, но и в потоке внутри сопла вблизи среза».
«Вид траекторий <...> соответствует и тому факту, что в застойных зонах вблизи стенки отверстия измеренное статическое давление равно входному давлению, а на уровне радиуса отверстия в том же сечении избыточное давление стремится к нулю либо становится отрицательным.»
Далее Котоусов отмечает (подтверждая математическими выкладками), что уже внутри сопла статическое давление уменьшается за счет зависимости продольной и поперечной составляющих скорости от соответствующих координат, обусловленных ускорением движения по мере приближения к срезу сопла. Кроме того, он отмечает перекрестное влияние этих составляющих, причем вблизи среза радиальная скорость уже практически не зависит от продольной координаты и изменяется очень мало, а вот изменение продольной скорости по радиусу с учётом радиальной компоненты скорости «дает существенный вклад в продольное снижение давления».
Затем Котоусов приводит экспериментальную оценку средней плотности компактной (монолитной) части струи после сжатого сечения, исходя из измеренных значений её диаметра, расхода и скорости. На расстоянии от 5 до 50 см от среза при средней скорости 28.3 м/с средняя плотность получилась приблизительно равной 620 кг/м3 (как известно, плотность спокойной воды в диапазоне температур от 0°С до 50°С составляет от 1000 кг/м3 до 990 кг/м3). Оценочный расчёт, выполненный им по полученным в ходе анализа формулам, дал примерно такую же плотность (620 кг/м3) и показал, что давление в струе (при сохранении высокой плотности) должно было бы быть на 0.5 атм ниже давления вакуума. Поскольку это физически невозможно, в струе возникают сильные кавитационные процессы, намного снижающие её среднюю плотность и обеспечивающие очень низкое давление в её середине. Чуть дальше он отмечает, что «в опытах регистрировалось абсолютное давление в струе на уровне 500 .. 150 Па при входных избыточных давлениях около 105 Па и выше».
После этого Котоусов анализирует роль газовыделения и кавитации, неизбежных в подобных условиях. Он отмечает, что выделение даже 10% атмосферных газов, растворённых в воде до равновесной концентрации при нормальных условиях, способно снизить плотность струи на 10–20%. Однако этого недостаточно для снижения плотности до 620 кг/м3. Вместе с тем его оценка кавитационного парообразования при давлении в 540 Па и температуре 8°С (равновесное давление паров воды для этой температуры составляет 1070 Па) показывает, что переход в парообразное состояние лишь 1 миллионной доли воды способен снизить среднюю плотность до 800 кг/м3, а 2 миллионных долей — до 680 кг/м3, что близко к измеренным значениям. Отсюда Котоусов делает закономерный вывод: «таким образом, поток в сопле и струя воды "разбухают" вследствие газовыделения и кавитации».
Будучи хорошим специалистом в классической термодинамике, Котоусов обращает внимание, что кавитационное парообразование должно немного уменьшить температуру среды, а это «вызывает значительное дальнейшее снижение давления и поддержание кавитации». По его оценке, кавитационное испарение 1 миллионной части воды с температурой 9°С вызывает снижение температуры на 0.0006°С, что при плотности паро-водяной смеси 800 кг/м3 должно вызвать дополнительное падение давления почти на 1.2 атм (правда, он отмечает возможность преувеличения подобной оценки). Тем не менее, он считает, что «несомненно, дополнительное снижение статического давления из-за температурного эффекта при испарении является одним из важных факторов, усиливающих кавитацию и повышающих скорость струй».
Почему же на достаточно большой длине струя сохраняет свою форму и видимую монолитность, хотя её усреднённая плотность значительно меньше плотности спокойной воды? Котоусов утверждает: «практическое постоянство диаметра струй до расстояний 0.7 м от среза сопел означает, что нормальная составляющая напряжения, действующего на струю со стороны воздуха, как раз компенсирует возмущение струи касательными напряжениями. Последние будут превалировать там, где струя начинает заметно расширяться, т. е. на расстоянии 1.2 .. 1.5 м от среза. Вместе с тем выравнивание давления по поперечнику струи происходит относительно медленно вследствие сравнительно низкой скорости распространения волны возмущения в двухфазной среде вода-воздух и вода-пар. Это — известный эффект Вуда».
В результате получается следующий механизм: «воздух стремится обжать струю, имеющую пониженное статическое давление, после среза сопла. Это приводит к увеличению ее скорости, к поддержанию процессов газовыделения, кавитации в приосевой части струи и т. д. На некоторой длине струи должно происходить постепенное выравнивание ее статического давления с давлением воздуха. По-видимому, полное выравнивание практически наступает там, где струя начинает заметно расширяться»
При этом Котоусов отмечает баланс разрывающих струю и сжимающих её механических усилий: «сходящиеся элементарные струйки для сопла №1 и отверстия в стенке перед срезом сталкиваются друг с другом, т. е. обмениваются нормальными составляющими импульса. До среза эти импульсы гасит стенка сопла, а после среза — разность давлений между воздухом и струей. Следует также учитывать, что взаимодействие струй является частично неупругим».
Котоусов об энергетическом балансе в обнаруженном эффекте
Единственным источником дополнительной энергии струи Котоусов видит внутреннюю энергию окружающего её воздуха. Он отмечает «следующие вклады энергии в кинетическую энергию струи:»
-
«уменьшение потенциальной энергии водного потока в гомогенном и гетерогенном состояниях согласно уравнению Бернулли, в котором плотность следует понимать как среднюю интегральную плотность на участке от входа в сопло до сжатого сечения» — это традиционный разгон струи под действием избыточного давления на входе сопла;
-
«уменьшение внутренней энергии окружающего струю воздуха атмосферы», — это новый, ранее неизвестный источник энергии струи. Эта энергия тратится на:
2.1) преодоление нормальных компонентов импульса элементарных струек, сталкивающихся друг с другом на участке от среза до сжатого сечения,
2.2) сжатие струи на участке от среза до сжатого сечения,
2.3) восстановление статического давления в струе до уровня давления атмосферы.
Таким образом, основным участком дополнительного разгона струи Котоусов считает участок её сжатия — от среза сопла до сжатого сечения. Он отмечает, что «на технически полезном участке струи от 5 до 50 см от среза ее кинетическая энергия практически постоянна для рассмотренных сопел. Поэтому обменом энергией воздуха со струей здесь можно пренебречь, но в конечном итоге его следует учитывать».
Рассматривая возможность использования реактивной силы отдачи сопла, Котоусов подчёркивает, что «на опыте она близка к расчетной величине для идеальной жидкости, если скорость на срезе сопла рассчитывать по уравнению Бернулли в одномерном приближении, предполагая, что статическое давление в струе на срезе близко к атмосферному», т.е. не обеспечивает дополнительной энергии по сравнению с той, что была затрачена на нагнетение жидкости в сопло. Это не удивительно, так как дополнительную энергию струя получает уже в воздухе — после прохождения среза сопла, — а значит, струя дополнительно разгоняется именно там, и этот разгон практически не воздействует на оставшееся позади сопло. Поэтому «понимание действительных свойств струи позволяет увеличивать силу отдачи при добавлении к соплу простого приспособления».
Почему эффект Котоусова не был обнаружен раньше?
Как же могло случится так, что за более чем 100 лет активного развития гидродинамики как науки столь важный эффект не был никем обнаружен и изучен? Естественно, Л.С.Котоусов не мог не задуматься над этим вопросом. В конце статьи он пишет: «следует подчеркнуть, что в известной нам литературе нет данных по непосредственному измерению средней скорости струй воды с поперечным размером в несколько миллиметров при скоростях струй более 10 м/с. Приводимые <в литературе> данные относятся к потокам в трубах в крупных энергетических установках. Нам не удалось измерить скорость струи с помощью трубки Пито, поскольку введение капилляра навстречу струе вызывает проскок воздуха с атмосферным давлением ко входу в капилляр (именно потому, что в струе отрицательное избыточное давление) и к искажению локальных параметров струи. Для течения в соплах либо течения перед насадками или отверстиями в стенках общепринято применение уравнения Бернулли в одномерном приближении. Из данного исследования вытекает, что в потоках жидкости с переменным сечением этого делать нельзя, а статическое давление в сжатом сечении всегда ниже атмосферного давления либо давления в окружающей сопло среде».
Отмечу, что во времена становления гидродинамики — на рубеже XIX и XX веков — не существовало миниатюрных тензодатчиков и не было возможности непосредственно измерять скоростной напор в разных точках потока малого сечения без внесения серьёзных возмущений в течение этого потока. Традиционные механические манометры могли дать лишь обобщённые результаты, весьма грубые относительно небольших сечений, а используемые в те времена трубки Пито, как было сказано выше, в силу своей конструкции не могли показать истинную картину. В то же время традиционное одномерное уравнение Бернулли давало достаточно близкие к фактическим результаты за исключением заниженных значений скорости и кинетической энергии струи, однако, если кто-то из исследователей и заметил это, то скорее всего списал на ошибки в измерениях, а средств для уточнённой проверки тогда не существовало. Кроме того, после создания основ гидродинамики фокус интересов учёных в соответствии с требованиями техники сместился либо в область изучения мощных потоков (трубопроводы и большая энергетика, кораблестроение и самолётостроение), где по мере увеличения диаметра струи влияние обнаруженного Котоусовым эффекта существенно снижается и, по-видимому, уже довольно быстро попадает в рамки погрешностей измерений, либо в область слишком маленьких струек (форсунки и пр.), где действие эффекта Котоусова может быть ослаблено другими факторами, да и основное внимание обычно обращают на совсем иные параметры (скажем, равномерность распыления и форму его факела, размеры капель т.п.), а кинетическая энергия монолитной части струи мало кому интересна.
Наконец, возможно, что заметные проявления эффекта иногда приписывались другим причинам: «кажущийся высоким по сравнению с воздушной турбиной собственный КПД ковшовой гидротурбины фактически обязан возрастанию мощности потока воды в сопле, питающем турбину. Скорость водяной струи из этого сопла нигде не проверялась экспериментально, а рассчитывалась по уравнению Бернулли в одномерном представлении».
Ограничения и использование эффекта Котоусова
Итак, под «эффектом Котоусова» я предлагаю понимать обнаруженное и описанное им явление, заключающееся в том, что кинетическая энергия струи, свободно истекающей в воздух из отверстия небольших размеров под действием избыточного давления, существенно (до нескольких раз) превосходит потенциальную энергию, обусловленную избыточным давлением в резервуаре с учётом расхода вещества. Степень проявления эффекта зависит от многих параметров, в том числе в значительной степени — от профиля сопла.
Однако прежде чем обсуждать перспективы и способы использования этого эффекта, считаю необходимым ознакомиться с ещё одной точкой зрения на его природу, отличной от точки зрения первооткрывателя.
Е.И.Андреев об эффекте Котоусова
Е.И.Андреев, известный не только поддержкой и развитием гипотезы Д.Х.Базиева об электрино и «фазовых переходах высшего рода» (ФПВР), но и реализованной на её основе модификацией двигателя «Жигулей» для безтопливной работы (точнее, для использования в качестве топлива обычного воздуха), также не обошёл вниманием работу Л.С.Котоусова. Андреев предполагает несколько иной механизм эффекта Котоусова. Вот его версия этого механизма.
«Монотонно текущих физических процессов вообще не бывает, так как они всегда идут под действием движущих сил, в частности, разности давлений, а эта разность не остается постоянной вследствие ее уменьшения первой же порцией протекшей воды. Возникает пульсирующее движение, волновое, колебательное. Эти малые возмущения получают быстрый разгон до звуковой скорости за счет природных сил колеблющихся молекул. Звуковые волны, имея на своем фронте повышенное давление, движутся со значительной скоростью, например, 1500 м/с, от источника возмущения в сторону меньшего давления. Эти прямые звуковые волны идут со всех сторон в радиальном направлении от периферии к оси струи. Сходясь с большой относительной скоростью (3 км/с), да еще с большими давлениями на своих фронтах, они соударяются, образуя взрыв, в данном случае — гидроудар. Это поперечный радиальный гидроудар в отличие от продольного гидроудара, впервые исследованного Н.Е.Жуковским. В результате взрыва образуются новые, обратные, волны, уже не звуковые, а ударные, разлетающиеся в обратном направлении со скоростью, которая выше скорости звука в данной среде. Взрывной уход масс вещества из эпицентра взрыва создает в нем вакуум, который, в свою очередь, вызывает новую центростремительную волну. Возникают колебания воды в струе, которые, например, хорошо видны на фотографиях струй, выполненных скоростной съемкой. При этом видно, что поверхность свободной струи взъерошена, имеются мелкие капельки над ее поверхностью, но калибр — диаметр струи остается постоянным, соответствующим диаметру выходного отверстия насадка. То есть струя не сжимается атмосферным давлением, а только разгоняется под действием ударных волн за счет атмосферного давления. В наибольшей мере это проявляется в конических сходящихся насадках, видимо, за счет более существенных возмущений, получаемых водой, при уменьшении сечения канала в зависимости от формы насадка, по сравнению с прямыми или расходящимися насадками.
 Скоростная фотография истечения свободной струи в воздух (вода движется слева направо). М.Ван-Дайк. Альбом течений жидкости и газа (М., Мир, 1986, фото №180).
Процессы энергообмена и накачки энергией имеют единый физический механизм во многих идентичных технических устройствах: конических сходящихся и других насадках, эжекторных соплах и системах, во вращающихся потоках, прямоточных реактивных двигателях и обыкновенных паяльных лампах. Малые возмущения от обжатия потока по мере его движения являются источником звуковых волн, имеющих на своих фронтах повышенные параметры (плотность, давление...). Волны своими фронтами как микрокувалдами оказывают ударное действие на струю, разгоняют ее, давая дополнительную избыточную энергию и мощность. Энергия пополняется извне — от внешней среды — путем электродинамического частотного взаимодействия молекул, в том числе, с участием электрино — посредника при сближении молекул на расстояние меньше критического, как в газах, жидкостях, так и в кристаллических решетках твердых тел.»
Учитывая, что гидроудары, возникающие, в частности, и при кавитации, Андреев рассматривает как одно из условий, которые могут вызвать ФПВР, именно ФПВР и является основным источником дополнительной энергии струи. При этом, как известно, ФПВР по Базиеву и Андрееву представляет собой разновидность ядерной реакции с микроскопическим дефектом массы атомов-участников (миллионные доли процента). Однако при постоянном «использовании» этот дефект постепенно нарастает, в результате чего уже меняются химические и физические свойства атома. В то же время сколько-нибудь заметными излучениями (по крайней мере заметными на фоне естественного фона) подобные ФПВР не сопровождаются — в частности, разновидностью подобного ФПВР является обычное горение. Дополнительно следует отметить, что эффект Котоусова по Андрееву должен сопровождаться ультразвуковым шумом, вызванным постоянным схлопыванием и разлётом вещества в центре струи в отличие от достаточно тихого, плавного и монотонного истечения по Котоусову. Кроме того, на фотографии хорошо видно, что основная зона микроударов, вызывающих «взъерошеность» струи, расположена не в сопле и не возле его среза, а на некотором расстоянии от него. Именно в этой зоне создаются оптимальные условия для ФПВР — там и происходит основной прирост энергии струи по Андрееву.
Но так ли важно, какой именно механизм вызывает эффект? Для кратковременных опытов — нет, но для долговременной эксплуатации установки на этом эффекте — да. В таблице приведено сравнение особенностей длительной работы такой установки в замкнутом рабочем цикле с изоляцией от внешней среды.
| Параметр |
Версия Л.С.Котоусова |
Версия Е.И.Андреева |
| Источник дополнительной энергии |
Внутренняя энергия (теплота) окружающего струю воздуха. |
ФПВР в зоне кавитации внутри струи. Частично возможно использование внутренней энергии окружающего струю воздуха. |
| Теплообмен системы с окружающей средой |
Нет (при условии использования всей полученной энергии внутри замкнутой системы, включая потери на трение). |
Необходим теплоотвод в связи с неизбежным образованием дополнительной тепловой энергии. |
| Время работы без отбора энергии в полезную нагрузку |
До механического износа деталей. |
Необходима периодическая (раз в несколько недель, месяцев или лет — в зависимости от периода обращения) замена рабочего тела в связи с утратой им первоначальных свойств. |
| Параметры отверстия сопла (см. ниже) |
Существует оптимальный размер. Наилучшая форма отверстия сопла — плоская. |
Существует оптимальный размер. Наилучшая форма отверстия сопла — круглая. |
Очевидно, что версия Котоусова позволит иметь практически идеальный «вечный двигатель», использующий рассеянную теплоту внешней среды, который при замкнутом рабочем цикле вообще может быть полностью изолирован от внешней среды и работать неограниченно долго. В то же время версия Андреева потребует охлаждения установки и периодической замены рабочих веществ. К сожалению, в этом неидеальном мире я склоняюсь к точке зрения Андреева, тем более вытекающие из его гипотезы эффекты соответствуют замечаниям Шаубергера и Клема о работе своих установок, включая постепенное исчерпание «энергопроизводящей способности» рабочих веществ и изменение состава химических элементов при длительной работе в замкнутом цикле. Впрочем, окончательный ответ могут дать только эксперименты. Пока же при рассмотрении этого эффекта я буду отмечать различия для этих версий, если они влияют на те или иные параметры установки.
О размерах и форме сопла
Как уже упоминалось выше, для хорошего проявления эффекта Котоусова необходимо выдерживать определённый диаметр струи. Как слишком толстая, так и слишком тонкая струя не будет обеспечивать максимальной эффективности, то есть соотношения полученной и затраченной энергий. Существенное значение может иметь и форма просвета сопла.
К сожалению, в статье не приводятся данные зависимости q от диаметра отверстия сопла, также как нет и конкретных данных о влиянии на проявление этого эффекта формы просвета сопла.
Размер имеет значение
Можно ли увеличить диаметр струи для повышения выхода дополнительной энергии? Как известно, при изменении линейных размеров с сохранением пропорций площадь геометрической фигуры меняется в квадратичной зависимости, а объём (и обусловленная им масса) — в кубической. Таким образом, при увеличении геометрических размеров струи отношение площади её поверхности к объёму уменьшается в обратной пропорции. А поскольку, по Котоусову, дополнительную энергию струе придаёт её обжим внешним воздухом, воздействующим, естественно, на её поверхность, то увеличение размеров ведёт к пропорциональному уменьшению удельной дополнительной энергии, т.е. доли этой дополнительной энергии, приходящейся на то же количество воды. Следовательно, при увеличении диаметра струи «КПД» установки будет снижаться (хотя в абсолютных величинах прирост будет иметь место). А так как гидравлические потери обычно пропорциональны площади поверхности трения, то они будут расти в квадратичной зависимости от линейных размеров и достаточно быстро «съедят» весь прирост энергии, а потом сделают общую эффективность установки отрицательной (ведь воду к соплу необходимо подавать, и подавать под достаточно большим давлением).
Если же верно предположение Андреева, то основное действие должно происходить в центральной зоне струи, где сталкиваются радиальные струйки. В таком случае очевидно, что объём этой зоны мало зависит от общего диаметра струи, поэтому при увеличении её диаметра падение удельной дополнительной энергии будет круче линейной зависимости, и эффективность установки сойдёт на нет ещё быстрее, чем в предыдущем случае.
Почему же Котоусов отмечает ковшовую гидротурбину (она же турбина Пелтона)? Ведь эти агрегаты относятся к «большой энергетике» — работают при давлениях минимум 20 атм (обычно — от 50 атм и выше, вплоть 180 атм) при расчётной скорости потока в форсунке до 150 м/с и расходе воды до 100 м3/с. Однако сама струя из форсунки имеет достаточно небольшой диаметр — для указанных расхода и скорости потока её диаметр составит всего 7.5 см (сечение около 44 см2) — не так уж много, кроме того, как мы увидим дальше, высокое давление и обусловленная им большая скорость потока могут существенно повысить абсолютный выход дополнительной энергии и сделать вклад эффекта Котоусова вполне заметным. Наконец, эти агрегаты обычно достаточно скоростные — до 3000 об/мин (50 об/с), что при числе ковшей-лопаток порядка 40 на одном колесе обеспечивает лишь 0.05 м3 (50 л) на каждую лопатку за один оборот. С учётом достаточно большой площади поверхности развёртки лопатки (скажем, 30 см · 70 см = 2100 см2) толщина слоя воды на лопатке составит порядка 2 см, а то и менее — а здесь эффект Котоусова может проявиться достаточно заметно и при истечении в лоток, каковым в данном случае является лопасть-ковш. Тем более, что конструктивные особенности турбины Пелтона позволяют использовать дополнительную энергию струи, полученную ею как на пути от форсунки до гребня-лезвия лопасти, так и при прохождении достаточно большого пути по поверхности самой лопатки.
Лучше меньше, да лучше?
Но следует ли из вышесказанного, что надо стремиться к наименьшему диаметру струи? С одной стороны, да. Но, с другой стороны, при уменьшении размеров струи возрастает отношение площади к объёму, а это приводит к возрастанию влияния таких факторов, как силы поверхностного натяжения и смачивания. В результате при диаметре струи порядка 1 мм их уже нельзя не учитывать, а при дальнейшем уменьшении струи они становятся определяющими, значительно тормозя истечение жидкости (как известно, при истечении из особо мелких отверстий после достижения некоторого порога скорость уже очень слабо зависит от разности давлений). Кроме того, в силу выросшего соотношения площади поверхности к массе воды, слишком тонкая струя гораздо легче разрушается сопротивлением воздуха, превращаясь в поток капель уже в непосредственной близости от среза сопла и имея очень короткую компактную (монолитную) часть, наиболее технически полезную в данном случае.
Таким образом, существует некий оптимальный диаметр струи, представляющий собой компромисс между двумя рассмотреными выше крайностями. Хотя Котоусов об этом прямо и не говорит, весьма вероятно, что для воды и круглых сопел оптимальным или близким к нему является подробно рассмотренный в статье диаметр сопла 4.6 мм, — ведь логично предположить, что исследовать эффект следует с теми параметрами сопел, при которых он проявляется сильнее всего, а не с теми, где он едва заметен...
Об оптимальной форме сечения струи
Л.С.Котоусов упоминает о том, что исследовались сопла различной формы, в том числе «с круглым, овальным и кольцевым выходными каналами». К сожалению, нет более подробных сведений о влиянии формы просвета сопла и, следовательно, сечения струи на выходе из него, на степень проявления обнаруженного эффекта. Тем не менее, здесь можно сделать несколько предположений.
Если эффект обусловлен обжатием струи внешним воздухом, то важно максимально увеличить отношение поверхности струи к её объёму. Для этого струю надо сделать как можно более плоской (при соблюдении некоей минимальной толщины, меньше которой влияние поверхностных сил будет слишком негативным). При этом увеличения мощности можно добиться, увеличивая ширину этой струи без изменения её толщины, тем самым сохраняя отношение площади к объёму практически неизменным и наращивая расход. Очевидно, что плоская струя в силу большей площади поверхности будет быстрее разрушаться воздухом, чем круглая с той же площадью сечения, однако на расстоянии нескольких сантиметров от среза сопла, где струя набирает практически всю дополнительную энергию, это не слишком актуально.
В случае же, если верно предположение И.Е.Андреева, то основное выделение энергии происходит в центре струи в зоне кавитации при обеспечении обжатия этой зоны радиальными струйками воды со всех сторон. В этом случае наиболее эффективной будет круглая форма сечения струи. Эта же форма в силу наименьшего соотношения площади поверхности и объёма струи обеспечит наибольшую длину компактной части, сведя к минимуму её разрушение из-за сопротивления воздуха.
О продольном профиле сопла
Хочу обратить внимание, что, судя по графику, именно сопло №1, являющееся, по утверждению Котоусова, аналогом самого простейшего случая — отверстия в тонкой стенке, — является для обнаруженного эффекта и наиболее оптимальным, — практически во всём диапазоне входных давлений и на разных растояниях от среза сопла. Очевидно, на него или на его аналог — обычное отверстие в плоской стенке (как наиболее простое и технологичное в изготовлении) и следует ориентироваться при практической работе с эффектом Котоусова.
И ещё один интересный факт. На этом графике коэффициенты q для всех сопел, кроме абсолютно «антиобтекаемого» ступенчатого №3, сближаются по мере приближения к давлению 3.5 атм. Можно предположить, что с ростом давления влияние различий профиля сопла на эффективность получения дополнительной энергии снижается, а коэффициент q (по сути, КПД эффекта Котоусова) стабилизируется в районе 3 .. 3.5.
О нагнетающем давлении
В отличии от размеров струи, для давления на входе сопла, нагнетающего жидкость наружу, в общем случае рекомендация однозначна — чем оно выше, тем большую дополнительную мощность с этого сопла можно получить. На первый взгляд, это противоречит приведённому Котоусовым графику зависимости q от входного давления. Однако вдумаемся, — ведь q — это параметр относительный, энергетическая эффективность, своего рода КПД эффекта Котоусова. И хотя по мере роста давления он несколько снижается, однако всё равно остаётся более чем в 2 раза больше единицы, а для некоторых типов сопел затем начинает несколько расти.
Что означает q > 2? Это означает, что на каждый джоуль, затраченный на нагнетание воды в сопло, в струе мы получим более 2 Дж энергии (правда, это без учёта потерь на трение). А значит, чем больше мощности мы «вкачиваем в накачку», тем больше дополнительной мощности (в абсолютном выражении) мы получим в струе! Таким образом, повышение давления (по крайней мере в исследованном Котоусовым диапазоне до 3.5 атм) однозначно выгодно, поскольку повышает абсолютный выход дополнительной мощности с сопла. Возможно, именно этим обусловлен тот факт, что в своём весьма мощном двигателе (около 350 л.с.) Ричард Клем использовал столь высокие давления (20 .. 35 атм). Кстати, чуть ниже мы увидим, что этим выгоды от повышенного давления не ограничиваются.
Об эффекте Котоусова в лотках и при разгоне воды без использования сопел
Частично свободное истечение струи — истечение в лоток — сплошь и рядом применяется в ирригации и «большой» гидротехнике (ГЭС, шлюзы). Но в более мелких масштабах, где проявление эффекта Котоусова наиболее заметно и может быть практически выгодно, такое встречается достаточно редко. Однако одним из перспективных способов использования эффекта Котоусова может быть совмещение сопла и лопатки, когда возможен именно такой режим истечения.
Истечение в лоток подобно истечению полностью свободной струи, однако не совсем — с одной или нескольких сторон струя ограничена стенками лотка. Поэтому на некотором расстоянии от отверстия истечения, когда струя достаточно тормозится о стенки лотка и окружающий воздух, скорость её понижается и уровень жидкости в лотке может быть выше, чем возле отверстия истечения (при большой скорости истечения — намного выше).
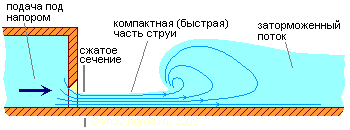 Истечение в лоток из-под затвора.
Традиционная гидродинамика отмечает, что при истечении в лоток также имеет место сжатие струи после прохождения отверстия, а значит, здесь действуют те же механизмы сжатия и удержания формы компактной части струи, что и при свободном истечении, но с одной поправкой — давление внешнего воздуха действует на струю не со всех сторон (а в показанном на рисунке случае и радиальные скорости тоже воздействуют лишь с одной стороны). Всё это может несколько ослабить проявление эффекта, причём как для версии его механизма от Котоусова, так и для гипотезы Андреева, однако в любом случае эффект должен продолжать существовать и в этих условиях.
А теперь рассмотрим ускорение воды без использования сопла. Случай весьма экзотический, но именно так устроена ATM Шаубергера — установка со спирально закрученными открытыми лотками-«рогами», сужающимися от центра к периферии вращения. Очевидно, что при вращении такого ротора в каждом спиральном лотке вода будет ускоряться за счёт центробежных сил — постепенно и без создания высокого давления. При этом движение воды в лотке должно вызывать эжекцию прилегающего к ней слоя воздуха, его ускорение, падение давления и, как следствие, — подсос свежего внешнего воздуха. И хотя здесь нет такого заметного радиального движения в сечении потока, как возле отверстия сопла, которому Котоусов и приписывал основную роль в сжатии струи, тем не менее по достижении определённой скорости возможны кавитационные явления и сжатие струи в лотке внешним воздухом — с передачей ей дополнительной энергии. Так что для механизма Котоусова в данном случае открытость спирального лотка имеет принципиальное значение.
А вот для механизма Андреева открытость лотка не так важна, а может быть, и вредна, поскольку «поджатие» внешним воздухом повышает давление в струе и ухудшает условия кавитации.
О влиянии закручивания струи
Раз уж зашла речь о Шаубергере, то стоит задуматься и о том, как может повлиять столь любимое им спиральное движение жидкости на проявление эффекта Котоусова. Как известно, при вращении жидкости в центре стремятся собраться не только лёгкие частицы и пузырьки растворённых газов, но, при определённых условиях, и частицы с плотностью большей, чем плотность основной жидкости. Кроме того, благодаря центробежным силам давление там будет меньше, чем на периферии вращения. В результате в середине спирально движущейся струи создаётся зона наибольшей неоднородности потока и наименьшей плотности струи. Это выгодно с точки зрения обоих механизмов — по Котоусову, за счёт менее плотного центра струи её обжатие воздухом после сопла может быть более эффективным, чем в случае лишь поступательного движения потока, а по Андрееву, пониженное давление и концентрация неоднородностей будут способствовать более интенсивной кавитации в
этой зоне и выработке большей дополнительной энергии за счёт вызванного этим ФПВР.
Однако и тут важно чувство меры. Слишком интенсивное закручивание струи приведёт к тому, что сразу после среза сопла её разорвёт на капли центробежными силами, и вместо монолитной струи с эффектом Котоусова мы получим вариант разбрызгивателя, в котором этот эффект использовать вряд ли удастся! Кроме того, слишком большие центробежные силы способны существенно снизить радиальную составляющую скорости жидкости перед срезом сопла — ведь на этом участке они прямо противодействуют давлению, нагнетающему жидкость в отверстие (от периферии вдоль торца радиально). Для сопел с внутренней конической поверхностью, где радиальная составляющая существенно меньше, чем в случае «отверстия в тонкой стенке», интенсивное спиральное закручивание потока может быть более эффективным, поскольку влияние отрицательных аспектов быстрого вращения будет ослаблено, а положительные сохраняются в полном объёме.
Возможно, по этим причинам вместо спирального вращения более эффективным может быть криволинейное истечение жидкости, когда зона разрежения и концентрации неоднородностей создаётся не по центру отверстия сопла, а асимметрично у внутреннего радиуса изогнутого канала (обратите внимание на форму каналов, образуемых периферийными лопатками внутри шаубергеровского репульсина). Имеющееся в статье Котоусова довольно туманное упоминание о том, что «при прочих равных условиях кривые сопла могут быть эффективнее прямых» может косвенно подтверждать этот вывод.
Оценка мощности струи под давлением
На какую же мощность можно рассчитывать? Попробуем вычислить мощность струи идеальной жидкости, истекающей в атмосферу по закону Торричелли — ту самую, относительно которой Котоусов рассчитывал свой коэффициент энергетической эффективности q.
Wт = m' · v2 / 2 = (S · v · ρ) · v2 / 2 = S · ΔP · √(2 · ΔP / ρ) (3.1),
где Wт — мощность истекающей струи, рассчитанная по закону Торричелли; S — площадь сечения струи; √ — операция извлечения квадратного корня; ΔP — давление жидкости перед отверстием, избыточное относительно внешней среды; ρ — плотность этой жидкости.
Как видим, рассчитанная по «классическим» законам мощность струи прямо пропорциональна площади её сечения, а изменение разности давлений влияет на неё ещё сильнее — пропорционально ΔP3/2 (круче линейной зависимости, но слабее квадратичной).
Для оценки порядка величин в таблице приведены результаты расчёта по этой формуле для воды (ρ = 1000 кг / м3; курсивом выделены данные для диаметра отверстия 4.5 мм, близкого к диаметру сопел, наиболее подробно исследованных Котоусовым).
Давление →
Диаметр ↓ |
5·104 Па (~0.5 атм) |
1·105 Па (~1.0 атм) |
1.5·105 Па (~1.5 атм) |
2·105 Па (~2.0 атм) |
3·105 Па (~3.0 атм) |
5·105 Па (~5.0 атм) |
7·105 Па (~7.0 атм) |
1·106 Па (~10 атм) |
2·106 Па (~20 атм) |
| 2.0 мм (3.14 мм2) |
1.57 Вт |
4.44 Вт |
8.16 Вт |
12.5 Вт |
23.1 Вт |
49.7 Вт |
82.2 Вт |
141 Вт |
397 Вт |
| 3.0 мм (7.07 мм2) |
3.53 Вт |
10.0 Вт |
18.4 Вт |
28.3 Вт |
51.9 Вт |
112 Вт |
185 Вт |
316 Вт |
894 Вт |
| 4.0 мм (12.6 мм2) |
6.28 Вт |
17.8 Вт |
32.7 Вт |
50.3 Вт |
92.3 Вт |
199 Вт |
329 Вт |
562 Вт |
1.59 кВт |
| 4.5 мм (15.9 мм2) |
7.95 Вт |
22.5 Вт |
41.3 Вт |
63.6 Вт |
117 Вт |
252 Вт |
417 Вт |
711 Вт |
2.01 кВт |
| 5.0 мм (19.6 мм2) |
9.82 Вт |
27.8 Вт |
51.0 Вт |
78.5 Вт |
144 Вт |
311 Вт |
514 Вт |
878 Вт |
2.48 кВт |
| 6.0 мм (28.3 мм2) |
14.1 Вт |
40.0 Вт |
73.5 Вт |
113 Вт |
208 Вт |
447 Вт |
741 Вт |
1.27 кВт |
3.58 кВт |
| 7.0 мм (38.5 мм2) |
19.2 Вт |
54.4 Вт |
100 Вт |
154 Вт |
283 Вт |
609 Вт |
1.01 кВт |
1.72 кВт |
4.80 кВт |
| 8.0 мм (50.3 мм2) |
25.1 Вт |
71.1 Вт |
131 Вт |
201 Вт |
369 Вт |
795 Вт |
1.32 кВт |
2.25 кВт |
6.32 Вт |
| 10 мм (78.5 мм2) |
39.3 Вт |
111 Вт |
204 Вт |
314 Вт |
577 Вт |
1.24 кВт |
2.06 кВт |
3.51 кВт |
9.93 кВт |
| Расчётная скорость струи (справочно) |
10.0 м/с |
14.1 м/с |
17.3 м/с |
20.0 м/с |
24.5 м/с |
31.6 м/с |
37.4 м/с |
44.7 м/с |
63.2 м/с |
| Справочные значения скоростей соответствуют красной линии (4) на графике из статьи Котоусова (зависимость скорости струи от избыточного давления). |
Чтобы получить мощность струи на расстоянии 5 .. 50 см от среза сопла, где эффект, по данным Котоусова, проявляется в наибольшей степени, значения из таблицы надо умножить на q, обычно лежащее в диапазоне от 2.5 до 4. Правда, для получения «чистой» дополнительной мощности необходимо умножать не на q, а на меньшую величину:
Wдоп = Wт · (q – 1 – η) (3.2),
где Wдоп — «чистая» дополнительная мощность струи; Wт — мощность истекающей струи, рассчитанная по закону Торричелли; q — КПД эффекта Котоусова; 1 — учёт мощности, необходимой для нагнетения идеальной жидкости до давления на входе сопла без учёта потерь; η > 0 — коэффициент дополнительных потерь, вызванных неидеальностью устройства (учитывает все виды трения и неидеальность нагнетателя).
Из этой формулы видно, что даже если невосполнимые потери на трение будут равны затратам энергии на идеальное нагнетание, всё равно при q > 2 можно рассчитывать на получение дополнительной мощности. Учитывая же весьма немалые мощности Wт, приведённые в таблице, особенно когда давление приближается к 10 атм, получаем очень интересный вывод: хотя следует учесть значительные потери в нагнетателе и на трение в реальных условиях, снижающие давление и скорость потока, то даже если их приравнять к прямым затратам на создание давления (η = 1, КПД нагнетателя должен быть более 50%), уже при q = 2.5 .. 3 и давлении порядка 20 атм суммарная мощность для двух-трёх десятков сопел вполне сравнима с заявленной Клемом (порядка 250 кВт).
Об импульсном режиме и гидроударах
Какой режим струи может быть выгоднее — постоянный или пульсирующий, с заметными паузами в истечении жидкости (по Андрееву, микропульсации присутствуют всегда, но сейчас речь не о них)?
Для ответа на этот вопрос сначала надо определить, в чём же различия между импульсным и постоянным режимами истечения — естественно, при одинаковом среднем расходе? Рассматривая гидроудар, мы выяснили, что с механической точки зрения происходит как бы концентрация кинетической энергии во времени без изменения её общего усреднённого количества. Однако при этом во время импульса эта «концентрация» обеспечивает существенное увеличение давления у входа сопла и скорости струи по сравнению с режимом постоянного истечения. На это и надо обратить внимание.
Что даёт такое повышение давление? С точки зрения механизма Котоусова, пожалуй, можно говорить лишь о наблюдаемом экспериментально снижении влияния внутреннего профиля сопла на степень проявления эффекта по мере роста нагнетающего давления. Более того, если давление станет слишком высоким и скорость струи превысит 1/4 .. 1/3 от скорости звука в воздухе, воздух может уже не успевать в достаточном количестве поступать к поверхности струи и не обжимать её в нужной степени, а это приведёт к снижению энергетической эффективности такого механизма. Но вот с точки зрения Андреева резкое повышение давления и скорости струи во время импульса должно вызвать более экстремальные условия в струе, а потому интенсифицировать ФПВР и увеличить выход полученной с его помощью дополнительной энергии — причём чем сильнее, тем больше!
♦
|