|
Практически во всех своих устройствах Виктор Шаубергер использовал сужающиеся каналы и подчёркивал, что именно такая форма обеспечивает разгон струи и получение дополнительной мощности. Я попробовал рассмотреть это утверждение с точки зрения механики, опираясь лишь на геометрические закономерности и классические законы сохранения импульса и энергии. И результаты, при выполнении всего одного дополнительного условия, подтвердили слова Шаубергера.
Простое движение жидкости в сужающейся трубе
Поведение жидкости при получении импульса внутри трубы
Цилиндрическая труба
Коническая труба
Ступенчатая труба
О вращении потока и особых условиях на оси трубы
Сначала рассмотрим движение однородной жидкости в трубе с сужающимся сечением с точки зрения традиционной гидродинамики.
В соответствии с законом непрерывности по мере сужения сечения трубы скорость сплошного (без разрывов и пузырей) потока внутри неё возрастает пропорционально этому сужению, то есть при сохранении пропорций профиля сечения — в квадратичной зависимости от уменьшения линейных размеров. При этом площадь контактирующих с жидкостью стенок сокращается в линейной пропорции, а сопротивление в соответствии с формулой Вейсбаха-Дарси с ростом скорости возрастает по квадратичному закону. В результате по мере уменьшения сечения трубы сопротивление течению жидкости нарастает и её движение всё более затрудняется.
Поскольку вся жидкость в трубе предполагается инертной и приводимой движение только внешней силой, по всей длине трубы она испытывает лишь сопротивление движению и торможение, которое из-за несжимаемости жидкости в полной мере передаётся на вход трубы. При этом сужение трубы увеличивает сопротивление и потому для улучшения пропускной способности при прочих равных условиях необходимо увеличивать диаметр трубы, и уж по крайней мере, не сужать её сечение.
Кроме того, из этого следует вывод о том, что продольный профиль трубы (цилиндрический, прямой конический, гиперболический и пр.) влияет лишь на то, насколько велика длина той части трубы, в которой поток испытывает наибольшее сопротивление, и не более того. В цилиндрической трубе жидкость тормозится равномерно по всей её длине, а в сужающейся основное сопротивление движению жидкости сосредоточено в наиболее узкой части трубы.
Теперь предположим, что находящаяся в трубе неподвижная жидкость получила импульс, причём не внешний (с того или иного торца трубы), а внутренний — в середине трубы по центру её сечения. При этом импульсное воздействие на жидкость вокруг «эпицентра» импульса направлено во все стороны равномерно (образуется сферическая «ударная волна»). Ситуация кажется фантастической, но технически реализуется достаточно просто — скажем, с помощью сконцентрированного локального нагрева лазерным лучом или СВЧ-излучением, мощность которого достаточна для вскипания жидкости в месте воздействия и вызывает давление образовавшегося пара на окружающие его области. Другой вариант — это схлопывание кавитационного пузырька, при котором после заполнения полости жидкостью возникает ударная волна, также распространяющаяся во все стороны. Есть и другие способы добиться такого эффекта.
Очевидно, что во всех этих случаях усилие от точки возникновения импульса распространяется во все стороны одинаково. При этом его составляющая, поперечная потоку, будет компенсирована реакцией стенок и в общем случае не окажет заметного влияния на течение жидкости, за исключением каких-то локальных эффектов. А вот влияние составляющих импульса, направленных вдоль оси трубы (как в одну, так и в другую сторону), может быть вполне заметным. Такую ситуацию мы и будем рассматривать в дальнейшем, уделяя внимание осевой составляющей полученного жидкостью импульса, считая, что к обоим частям потока («до» и «после» точки приложения импульса) прилагается одинаковое усилие, естественно, направленное в противоположные стороны.
Предположим, что вышеописанный импульс возник в геометрическом центре цилиндрической трубе. В соответствии с классической механикой обе части жидкости — и слева, и справа от места возникновения импульса — получат одинакое изменение количества движения (физический импульс), однако направлено оно будет в разные стороны. Соответственно и энергия, отданная обоим частям, будет одинакова.
Теперь представим себе, что точка возникновения импульса начала смещаться к одному из концов трубы. В этом случае в соответствии с законом сохранения импульса скорости левой и правой частей жидкости будут обратно пропорциональны их массе, которая в цилиндрической трубе определяется только длиной её соответствующего участка. Поэтому по мере приближения места воздействия импульса к срезу трубы скорость жидкости в сторону ближайшего среза будет возрастать, а в сторону противоположного среза — уменьшаться в линейной зависимости от координаты этого места.
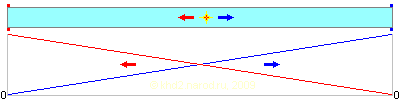 Изменение энергии и скорости жидкости в зависимости от места импульсного воздействия на неё внутри цилиндрической трубы. Цвет графика соответствует цвету торца трубы.
При этом кинетическая энергия обоих частей также будет меняться по линейному закону. На первый взгляд это кажется странным, но только на первый взгляд. Да, энергия пропорциональна квадрату скорости, но она пропорциональна и массе вещества, а в нашем случае увеличение скорости сопровождается соответствующим уменьшением массы движущейся в эту сторону жидкости — одна степень сокращается, — поэтому изменение энергии получается прямо пропорциональным изменению скорости.
В результате мы имеем перераспределение энергии импульса и скорости жидкости в сторону ближайшего среза трубы, и когда импульс приложен в непосредственной близости от этого среза, практически вся его энергия будет направлена именно в эту сторону. В общем же, если предположить, что подобные импульсы происходят по всей длине трубы с одинаковой вероятностью — неважно, по всему объёму жидкости или только по оси трубы, — мы получим абсолютно симметричную картину без какого-либо предпочтительного направления разгона жидкости.
Теперь допустим, что труба имеет коническую форму с линейной образующей. В этом случае точка, в которой имеет место равенство масс жидкости слева и справа от точки возникновения импульса (для краткости назовём её «точкой равновесия») смещается к широкому концу и определяется равенством
0l∫ π · R(x)2 dx = lL∫ π · R(x)2 dx (1),
где l — координата точки равновесия от начала трубы; L — полная длина трубы; R(x) — закон зависимости радиуса трубы от текущей координаты (функция образующей).
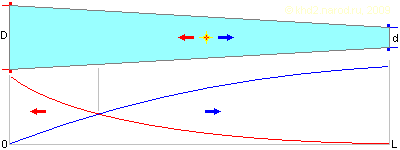 Изменение скорости жидкости в зависимости от места импульсного воздействия на неё внутри конической трубы. Цвет графика соответствует цвету торца трубы.
В нашем случае для линейной образующей
R(x) = (D – (D – d) · x / L) / 2 (2),
где R(x) — закон зависимости радиуса трубы от текущей координаты (функция образующей); D — большой диаметр (широкий торец трубы); d — малый диаметр (узкий торец трубы).
Введя коэффициент соотношения выходного и входного диаметров k = d / D, заменим d на D · k и возведём всё в квадрат:
R(x)2 = ((D – (D – D · k)) · x / L)2 / 4 = (D · (1 – x · (1 – k)) / L)2 / 4 = (1 – 2 · x · (1 – k) / L + x2 · (1 – k)2 / L2) · D2 / 4 (3).
Теперь после вынесения постоянных множителей из-под интеграла и их сокращения равенство (1) приобретает вид
0l∫ (x2 · (1 – k)2 / L2 – 2 · x · (1 – k) / L + 1) dx = lL∫ (x2 · (1 – k)2 / L2 – 2 · x · (1 – k) / L + 1) dx (4),
и после интегрирования превращается в
2 · (l3 · (1 – k)2 / (L2 · 3) – l2 · (1 – k) / L + l) = L3 · (1 – k)2 / (L2 · 3) – L2 · (1 – k) / L + L (5).
Сократив лишние L в правой части и перенеся всё в левую, получаем кубическое уравнение относительно l:
l3 · 2 · (1 – k)2 / (L2 · 3) – l2 · 2 · (1 – k) / L + l · 2 – L · ((1 – k)2 / 3 – (1 – k) + 1) = 0 (6),
после чего ещё раз преобразуем полученное кубическое уравнение, разделив всё на коэффициент при первом члене:
l3 – l2 · 3 · L / (1 – k) + l · 3 · L2 / (1 – k)2 – L3 · (3 · k / (1 – k)2 + 1) / 2 = 0 (7).
Для случая D = 2 см и d = 1 см k будет равно 0.5, а коэффициенты перед степенями неизвестного с третьей по нулевую а, b, с и d при L = 1 м соответственно получаются равными
a = 1; b = –6; c = 12; d = –7/2 = –3.5.
Решая уравнение l3 – 6 · l2 + 12 · l – 3.5 = 0, получаем l = 0.349 (решение имеет один вещественный корень и два комплексно сопряжённых, которые в данном случае физического смысла не имеют). При длине трубы L = 2 м и том же соотношении диаметров отверстий уравнение будет иметь вид l3 – 12 · l2 + 48 · l – 28 = 0 и его вещественный корень равен 0.698, то есть те же 34.9% от полной длины трубы (впрочем, ожидать иного результата было бы нелепо).
Очевидно, что для оценки различных продольных профилей труб удобно перейти от абсолютной длины трубы к относительному положению «точки равновесия» от широкого конца трубы, приравняв L к единице:
l3 – l2 · 3 / (1 – k) + l · 3 / (1 – k)2 – (3 · k / (1 – k)2 + 1) / 2 = 0 (8).
Если разность диаметров будет больше, то координата «точки равновесия» ещё больше сместится к широкому концу трубы. Скажем, для k = 1/3 уравнение (8) примет вид l3 – 4.5 · l2 + 6.75 · l – 1.625 = 0, что соответствует вещественному корню l = 0.295, а при k = 1/5 получим l3 – 3.75 · l2 + 4.6875 · l – 0.96875 = 0 с вещественным корнем l = 0.255.
Главный вывод, который следует из всей вышеприведённой математики, заключается в том, что точка, в которой импульс придаст одинаковую скорость жидкости с обоих сторон, существенно смещена к широкому концу конической трубы.
Что это нам даёт в смысле возможного направления течения жидкости при равномерно-случайном воздействии на неё подобных внутренних импульсов? Если вероятность возникновения импульса одинакова для любой точки жидкости — ничего, поскольку массы по обе стороны от найденного нами сечения равны, а следовательно, как и в случае цилиндрической трубы, возникновения направленного движения жидкости ожидать не следует.
Однако, если предположить, что импульсы возникают не по всему объёму жидкости, а лишь по её оси (хотя вероятность их появления в любом месте этой оси по-прежнему одинакова), мы получим направленное движение жидкости, причём движение это будет в сторону узкого конца конической трубы — ведь большую часть длины трубы занимает участок оси, где масса жидкости со стороны узкого конца меньше массы жидкости со стороны широкого, а значит преимущественное движение там будет к узкому концу!
Стоит отметить, что в соответствии с формулами (7) и (8) положение «точки равновесия» зависит не от абсолютного диаметра трубы, а лишь от соотношения входного и выходного диаметров. Как видно из приведённых выше цифр, если такое отношение равно 1:2, то отношение длины «толкающего» участка к длине «тормозящего» будет чуть меньше, чем 2:1. Для большей разницы диаметров эта разность длин также увеличится, однако при линейной образующей рассчитывать на даже на соотношение 4:1 не следует (при k → 0 уравнение (8) приобретает вид l3 – 3 · l2 + 3 · l – 0.5 = 0 с вещественным корнем l = 0.206, что соответствует соотношению 3.85 : 1).
Использование других типов образующей конуса, скажем гиперболы, при определённых условиях позволяет ещё больше сместить «точку равновесия» к широкому концу при том же соотношении диаметров входа и выхода трубы и, следовательно, ещё большую долю энергии импульсов направить на поступательное движение жидкости в сторону узкого конца трубы (правда, аналитический расчёт положения «точки равновесия» в этом случае будет сложнее, так как потребует решения уже не кубического уравнения, а уравнения более высокого порядка — в зависимости от формулы, описывающей образующую конуса).
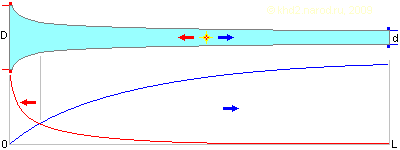 Изменение скорости жидкости в зависимости от места импульсного воздействия на неё внутри конической трубы с нелинейной образующей (утрировано). Цвет графика соответствует цвету торца трубы.
И, конечно, как и в любом деле, выбирая нелинейную образующую, важно соблюдать чувство меры. Кривизна нелинейной образующей должна быть тем меньше, чем меньше разница между диаметрами входа и выхода трубы, и даже при двукратном их соотношении оптимальный профиль этой образующей не очень сильно отличается от линейного. На рисунке хорошо видно, что если в начале труба будет сужаться слишком резко, то мы рискуем получить ту же цилиндрическую трубу, только с небольшой воронкой на конце! Очевидно, что такая конструкция с точки зрения «проталкивания» жидкости будет мало отличаться от симметиричной цилиндрической трубы. Зато, исходя из вышеизложенного, хорошие шансы на эффективное прокачивание даже при равенстве входного и выходного диаметров имеет труба, составленная из сегментов, продольный разрез которых показан ниже.
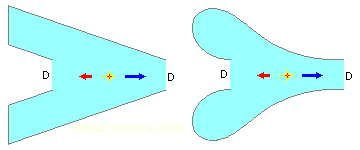 Варианты сегментов трубы со смещённой «точкой равновесия» и равными входным и выходным диаметрами. Слева — «техно», справа — «био». Ничего не напоминает?
Следует отметить, что конструкции, показанные на последнем рисунке, способны обеспечить направленное движение жидкости даже в том случае, если импульсные воздействия будут происходить не только на оси потока, но и во всём объёме жидкости.
Доведя изложенные выше соображения о продольном профиле трубы до логического конца, можно придти к выводу, что, если не прибегать к изготовлению сложных форм и пытаться обойтись стандартными изделиями заводского изготовления, наибольшей относительной длины узкой (разгоняющей) части можно добиться, ступенчато соединив две цилиндрические трубы — большого (входного) и малого (выходного) диаметров.
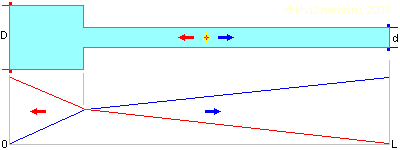 Изменение скорости жидкости в зависимости от места импульсного воздействия на неё внутри ступенчатой трубы, состоящей из двух цилиндрических труб. Цвет графика соответствует цвету торца трубы.
В этом случае соотношение длин широкой и узкой частей обратно пропорционально соотношению их площади сечений, то есть квадрату соотношения их диаметров. Например, для соотношения диаметров 2:1 соотношение длин будет 1:4 и «точка равновесия» будет находиться на расстоянии 20% общей длины от широкого входа (сравните с 34.9% для прямой конической трубы с тем же соотношением входного и выходного диаметров).
Недостаток ступенчатой трубы кажется очевидным — резкое изменение диаметра вносит дополнительное гидродинамическое сопротивление. Однако при небольших скоростях потока и не слишком сильном различии диаметров труб влияние этого фактора весьма мало. Кроме того, всегда можно несколько сгладить переход, как показано ниже.
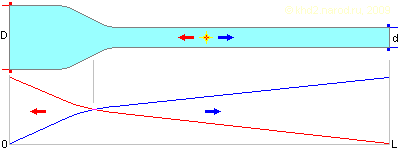 Изменение скорости жидкости в зависимости от места импульсного воздействия на неё внутри ступенчатой трубы со сглаженным изменением диаметра. Цвет графика соответствует цвету торца трубы.
Если поток движется по сужающейся трубе поступательно и ламинарно, то в каждом сечении трубы условия на его оси практически ничем не отличаются от условий в любой другой точке этого сечения (пожалуй, лишь за исключением самых крайних слоёв, испытывающих заметное торможение о стенки трубы). Однако стоит закрутить поток вокруг продольной оси, и различия условий в его центре и на периферии становятся заметными.
Благодаря центробежным силам в центре образуется область пониженного давления. Кроме того, там собирается и большинство неоднородностей, содержащихся в текущей жидкости — начиная от лёгких пузырьков растворённых газов и кончая достаточно тяжёлыми включениями, плотность которых может заметно превышать плотность самой жидкости. В результате на оси потока создаются наиболее экстремальные условия, которые могут спровоцировать проявление различных эффектов — от интенсификации химических реакций до возникновения кавитационных явлений.
Здесь я не хочу углубляться в дебри гипотез о причинах, которые могут вызвать механическое импульсное воздействие на струю воды непосредственно внутри потока, но вышесказанное однозначно подтверждает, что осевая зона потока — особенное место, поэтому рассмотренное выше предположение о том, что побуждающие импульсы могут быть не рассеяны по всему объёму жидкости в трубе, а сосредоточены в районе её оси, имеет право на существование.
Более того, по мере уменьшения диаметра трубы возрастает линейная скорость движения потока, но не только. При сохранении момента инерции вращающейся жидкости уменьшение радиуса вращения автоматически ведёт даже не к сохранению, а к увеличению угловой скорости потока, и условия на оси вращения становятся всё более экстремальными. В результате, если наши гипотетические импульсы вызваны именно подобными условиями, вероятность их появления ближе к узкому концу нарастает. А как раз там большая часть энергии этих импульсов «работает» на прокачку потока, а не на его торможение. Вот вам и «всасывающий эффект» шаубергеровских труб, зарегистрированный не только самим Шаубергером, но и его научным оппонентом профессором Поппелем!
♦
|