О неизбежности вращения в среде | Perpetuum mobile: «свободная энергия» и вечные двигатели.

Как известно, в реальном мире все объекты находятся не изолировано друг от друга, а во взаимодействии, т.е. в среде. Однако любая подвижная среда при наличии в ней внутреннего движения практически всегда испытывает завихрения. Очевидно, что это не случайно. Но можно ли обосновать закономерность возникновения внутреннего вращения при любом движении внутри подвижной среды, или это необходимо принять как постулат?

Причины возникновения завихрений в среде

В отличие от твёрдой среды, в которой положение образующих её объектов практически неизменно, в подвижной среде такой жёсткой фиксации элементов нет. Поэтому как только в такой среде возникает внутреннее движение, образующие её объекты начинают сталкиваться друг с другом. В результате этих столкновений их направление движения постоянно меняется.

Моделирование завихрений в плоскости

Рассмотрим эту ситуацию в простейшем случае. Предположим, что движение среды осуществляется в двухмерной плоскости, при этом каждое взаимодействие движущихся объектов приводит к изменению их траекторий на один и тот же угол (скажем, равный среднему углу изменения траектории в какой-то реальной среде) с равной вероятностью направо и налево. Попробуем проследить движение одного объекта. Кажется, что случайные повороты должны скомпенсироваться. На большом числе взаимодействий так и будет, но ведь для того, чтобы замкнуть круг, нужно повернуть в одну сторону не слишком много раз.

Какое движение можно считать линейным? Пожалуй, тут лучше пойти от противного. Вряд ли можно назвать линейным движение, в результате которого первоначальное направление изменилось на 90° и более, а также движение, в результате которого направление осталось близким к исходному или даже точно ему соответствует, но при этом продвижение в «основном» направлении равно перпендикулярному смещению или даже меньше него, то есть «вбок» объект сместился больше, чем «вперёд»! Таким образом, всё, что попадает под эти определения, следует отнести к вращательному движению, а уж является ли оно замкнутым вращением (вихревым) или это можно считать лишь «поворотом» траектории объекта — дело второе.

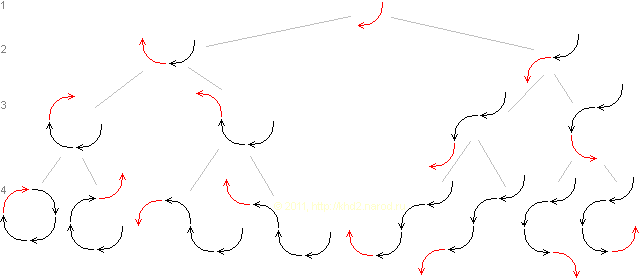Полный набор вариантов поворота траекторий на 90° в плоскости при равной вероятности левого и правого поворотов после первого поворота по часовой стрелке.

На рисунке показано полное дерево вариантов траекторий в случае поворота на 90° до первого замыкания траектории при равной вероятности левого и правого поворотов после первого поворота по часовой стрелке (при первом повороте против часовой стрелки картина зеркальная, и общие вероятности продолжения первоначального движения и замыкания траектории остаются теми же самыми). Что же мы видим? Из 8 вариантов в одном случае круг полностью замкнулся, в четырёх случаях движение пошло в обратном направлении, и лишь в трёх случаях оно продолжилось в прежнем направлении, но как минимум два из них никак нельзя отнести к прямому движению — в одном из них продвижения в исходном направлении вообще нет, а в другом оно равно смещению вбок. И лишь в одном случае из 8 продвижение в исходном направлении было больше боковых отклонений! При меньших углах поворота количество вариантов, прежде чем в одном из них кольцо замкнётся, естественно, намного больше, но в целом и там получается аналогичный расклад...

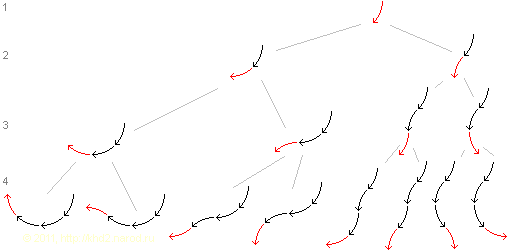Полный набор вариантов поворота траекторий на 45° в плоскости при равной вероятности левого и правого поворотов после первого поворота по часовой стрелке для последующих трёх столкновений.

Например, при угле поворота 45° уже через 4 поворота лишь 25% случаев можно отнести к условно линейному движению, а в 62.5% случаев направления движения уже изменилось не менее, чем на 90°. Таким образом, очевидно, что любое случайно-регулярное изменение траектории движения, неизбежное для движущихся частиц среды, ведёт к завихрениям траекторий! В трёхмерном пространстве вероятность своевременного «выправления» траектории и её самопроизвольного возвращения к относительно линейному движению ещё меньше. И лишь внешние ограничивающие факторы, такие как стенки узкой трубы, могут воспрепятствовать естественному завихрению движущейся среды.

О нестабильности завихрений

Завихрения траекторий возникают в результате ряда случайных событий, заворачивающих частицу преимущественно в одну сторону. Однако поскольку эти события случайны, рано или поздно возникает «компенсирующая» цепочка событий, которая «разворачивает» траекторию обратно. Если к этому времени частица уже успела совершить значительную часть оборота, или целый оборот, или даже несколько оборотов, то внешне это будет выглядеть как «разрушение» сформировавшегося было вихревого движения, а то и закручивание в противоположную сторону.

По этой причине в отсутствие каких-либо других внешних факторов, влияющих на закручивание движения или препятствующих этому, в движущейся подвижной среде завихрения всё время образуются и разрушаются, образуя ту самую картину, которую мы привыкли видеть в бурно текущем потоке. И для объяснения этого не пришлось привлекать «локальное исчерпание энергии» и тому подобные предположения! Локальное перераспределение энергии при завихрениях, безусловно, имеет место, но оно является следствием этих завихрений, а не их причиной!

Влияние скорости на радиус завихрения

Итак, завихрение в подвижной среде неизбежно. Однако как оно соотносится со скоростью движения этой среды? Очевидно, что имеется в виду лишь движение среды относительно непосредственно контактирующих с ней объектов — скажем, жёстких стенок или другой струи в той же среде. Если такого движения нет, то нет и вызванного им завихрения. (Закрепим две закупоренные бутылки с жидкостью на крыше автомобиля — одну подвесим изнутри, в закрытом салона, а другую установим снаружи, над внешней поверхностью крыши. После того, как автомобиль наберёт скорость, жидкость внутри бутылок будет вести себя одинаково, поскольку в обоих случаях она движется не относительно бутылок, а вместе с ними. В то же время воздух вокруг внешней и внутренней бутылок поведёт себя абсолютно по-разному, так как скорость бутылок относительно окружающего их воздуха будет совершенно разной.)

Из классической механики мы знаем, что чем больше линейная (тангенциальная) скорость вращающегося на подвесе тела, тем бóльшую силу надо приложить, чтобы сохранить прежний радиус вращения, так как центростремительное ускорение и центробежная сила растут пропорционально квадрату скорости вращения. А чтобы при росте скорости радиус вращения уменьшался, надо приложить ещё бóльшую силу — так что вроде бы нет причин для уменьшения радиуса завихрений при возрастании скорости среды. Однако именно это явление мы наблюдаем на границах струй — чем больше относительная скорость, тем меньше радиус образующихся вихрей и тем больше скорость вращения каждого из них! Почему это происходит, ведь это похоже на нарушение главного закона природы — стремления любых систем к конфигурации, соответствующей минимуму внутренней энергии, обычно сопровождаемой как можно более равномерным распределением энергии внутри системы?

Рассмотрим ситуацию подробнее. Как мы знаем, частицы подвижных сред в нормальных условиях (т.е. далёких от тех, что возникают при встрече пучков заряженных частиц в ускорителях) не испытывают механических столкновений друг с другом, а изменяют свои траектории в результате отталкивающего дистанционного электромагнитного взаимодействия образующих их элементарных частиц. При этом сила этого взаимодействия резко нарастает по мере сближения — вплоть до 6-й степени от сокращения расстояния (когда сближение в 2 раза увеличивает силу в 64 раза). В этой ситуации чем больше встречная скорость сближающихся частиц, тем ближе они смогут подойти друг к другу, прежде чем разойдутся врозь, и тем больше будет максимальная сила их взаимодействия. Может быть дело именно в этом?

Моделирование сближения отталкивающихся частиц

С помощью программы моделирования взаимодействия заряженных частиц попробуем воспроизвести ситуацию, направив две взаимно отталкивающиеся частицы с равными одноимёнными зарядами одинакового диаметра D навстречу друг другу с небольшим смещением их центров относительно друг друга Δ (ведь в реальности именно так и происходит, надо сильно постараться, чтобы центры частиц оказались точно на линии их сближения).

Встречное движение взаимно отталкивающихся частиц при смещении центров на 0.05 диаметра. Здесь и далее цвета соответствуют исходным скоростям в условных расчётных единицах расстояния и времени (р.е.р. / р.е.в.): красный — 1, жёлтый — 2, зелёный — 5, синий — 10, сиреневый — 20. Чёрными кружками отмечено исходное положение частиц.

Разберём первый эксперимент. Скорости подобраны так, что при среднем значении (зелёная траектория) частицы сближаются друг с другом почти вплотную, но до механического столкновения дело не доходит. В этом случае угол отклонения от начальной прямой будет наибольшим. Чем сильнее скорость отличается от оптимальной как в меньшую (жёлтая и красная), так и в бóльшую сторону (синяя и сиреневая), тем меньше линия траектории отклоняется от исходной. В первом случае это обусловленно возрастанием расстояния останова и потому малым углом максимального отклонения линии взаимодействия от линии траектории, а во втором — слишком быстрым сближением, за время которого отклоняющая сила не успевает оказать существенного влияния на изменение траектории, и траектория меняется в основном за счёт механического взаимодействия. Поскольку в реальности механические столкновения частиц среды (атомов и молекул) требуют слишком высокой скорости сближения, не достижимой в нормальных условиях, на дальнейших иллюстрациях случаи механического столкновения не показаны.

Встречное движение взаимно отталкивающихся частиц при смещении центров на 0.1 диаметра. Скорости, при которых происходит механическое соприкосновение частиц, из результатов исключены.

Встречное движение взаимно отталкивающихся частиц при смещении центров на четверть диаметра. Скорости, при которых происходит механическое соприкосновение частиц, из результатов исключены.

Встречное движение взаимно отталкивающихся частиц при смещении центров на половину диаметра. Скорости, при которых происходит механическое соприкосновение частиц, из результатов исключены.

Встречное движение взаимно отталкивающихся частиц при смещении центров на 1 диаметр.

Встречное движение взаимно отталкивающихся частиц при смещении центров на 2 диаметра.

Встречное движение взаимно отталкивающихся частиц при смещении центров на 5 диаметров.

По всем вариантам моделирования, когда расхождение центров не превышает диаметра частиц, можно сказать одно и то же: чем выше скорость, тем больше угол отклонения отскока от линии исходной траектории (я говорю об угле именно между линиями, а не направлениями, поскольку как раз этот фактор является определяющим для закручивания среды — отражение строго назад (угол 180°, направления противоположны, линии совпадают) приводит не к закручиванию, а лишь к возвратно-поступательному движению). Поэтому скорость сближения, обеспечивающую максимальное сближение частиц при «лобовом» столкновении, но при которой ещё не возникает механического контакта, можно назвать критической. Ещё раз подчеркну, что в реальных условиях достичь такой скорости практически невозможно, — все скорости движения частиц намного меньше критической. А значит, правило «чем выше скорость, тем больше угол отклонения при взаимодействии и, соответственно, меньше радиус завихрения» в этих условиях действует всегда. При этом можно заметить, что угол отклонения возрастает примерно пропорционально исходной скорости. А поскольку с ростом скорости при сохраняющейся концентрации частиц интервал между столкновениями сокращается обратно пропорционально скорости (средний пробег между столкновениями остаётся прежним), диаметр завихрений в движущейся среде должен быть обратно пропорционален скорости движения — чем выше скорость, тем меньше диаметр, что мы и наблюдаем в реальности.

Ситуация несколько меняется, когда смещение центров превышает диаметр частицы — тогда скорость наибольшего отклонения становится меньше критической и начинает постепенно снижаться, так как время взаимодействия при больших скоростях становится слишком маленьким для максимального разворота от линии исходной траектории. При этом по результатам моделирования скорость, для которой достигается максимальное отклонение v_mo примерно соответствует критической скорости, умноженной на квадратный корень из отношения диаметра частиц к смещению их центров от линии начального взаимодействия: v_mo = v_кр · √ D / Δ (напомню, что в данном случае сила взаимодействия рассчитывалась по закону Кулона, т.е. убывала обратно пропорционально квадрату расстояния).

О разрежении внутри вихря

Довольно широко распространено мнение, что закручивание вихря обуславливается разрежением, возникающем в его центре из-за центробежного отброса вещества к периферии. Мол, при этом возникает разность давлений, которая и заворачивает вращающееся вещество. Это неверно и не имеет ничего общего с действительностью!

В самом деле, разрежение в центре не может превышать абсолютного вакуума и потому конечно. Более того, в подавляющем большинстве реальных вихрей, включая бешенно вращающиеся торнадо, оно хотя и велико, но к вакууму не приближается и близко, вполне позволяя дышать людям и животным. Поэтому по мере нарастания скорости вращения сжатие радиуса вращения должно сходить на нет, и весьма быстро, чего в реальности не наблюдается. Кроме того, это никак не объясняет, что мешает внешним стенкам вихря «разлетаться» наружу, тем самым быстро разрушая вихрь. В то же время рассмотренный выше механизм зависит не от условий в середине вихря, а лишь от разности скоростей на границе струй, и чем больше эта разность, тем эффективнее действует этот механизм, уменьшая радиус вихря и делая более чёткой его границу, что как раз и имеет место в реальности.

Таким образом, разрежение в середине вихря является следствием вращения, а не его основной причиной, хотя оно и может вносить свою лепту, в некоторых условиях вполне заметную.