О причинах разлёта и объединения частиц газа
Главный вопрос, возникший уже при первых наблюдениях за поведением скопления «сводобных атомов», был совершенно очевиден: почему электрически строго нейтральные «атомы» и «молекулы» испытывают столь явно выраженное взаимное отталкивание, каков механизм их разлёта? С другой стороны, почему «атомы» всё же стремятся объединиться друг с другом, а не разлетаются по одиночке?
Механизм взаимного отталкивания и разлёта
Электростатический подход
Электродинамический подход
Взаимное притяжение
И притяжение, и отталкивание
Взаимодействие множества свободных объектов с неравномерным распределением зарядов
Взаимная ориентация
Изменение распределения зарядов
Моделирование взаимодействия
Некоторые выводы о взаимодействии свободных объектов с неравномерным распределением зарядов
Следствия из электрической природы взаимодействия частиц газа
О зависимости силы взаимодействия от расстояния
Линейная зависимость силы взаимодействия от расстояния
Поправки Ван-дер-Ваальса
Отступление от темы
Смотреть шире!
Механизм взаимного отталкивания и разлёта
После небольшого размышления ответ стал казаться очевидным, и следовал он из самого обычного закона Кулона, известного любому выпускнику неполной средней школы (по крайней мере теоретически это должно быть именно так)!
Электростатический подход
Дело заключается в том, что хотя «атомы» и являются электрически нейтральными, они состоят из дискретных зарядов, разнесённых в пространстве. В результате возникает некоторый дисбаланс сил взаимодействия образующих их зарядов. Безусловно, возникающие силы отталкивания намного меньше, чем если бы разность зарядов составила хотя бы один заряд «электрона». Но всё же это оказывается принципиально важным обстоятельством не только на расстояниях, сравнимых с размерами атомов, но и гораздо бóльших.
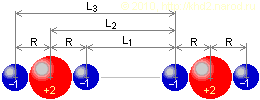 Иллюстрация к электростатическому объяснению механизма разлёта молекул «газа».
На рисунке показаны два одинаковых «атома», каждый из которых имеет два «электрона» с отрицательным единичным зарядом и ядро с зарядом +2, так что каждый «атом» является электрически нейтральным. Расположим их так, как показано на рисунке (все заряды лежат на одной прямой), и получим аналог взаимодействия окружённых электронными оболочками ядер «атомов» в нашем эксперименте. Примем расстояние между центром ядра и центром электрона равным R, а расстояние между центрами ближайжих друг к другу электронов разных атомов L1. Тогда, соответственно, L2 = L1 + R, а L3 = L1 + 2 · R.
Для расчёта силы воздействия одного такого «атома» на другой используем закон Кулона F = k · Q1 · Q2 / r2. Здесь Q1 и Q2 — взаимодействующие заряды, а r — расстояние между ними. Коэффициент k зависит от используемой системы единиц измерения: в системе СГCЭ он просто обратен абсолютной диэлектрической проницаемости k = 1 / εa, а в системе СИ он равен 1 / (4 · π · εa).
На ближний к соседнему «атому» электрон с единичным зарядом qe будет воздействовать сила
Fe1 = –k · qe2 / L12 + k · n · qe2 / L22 – k · qe2 / L32 (1),
где q — заряд электрона; L1, L2, L3 — соответственно расстояния до ближнего электрона, ядра и дальнего электрона соседнего атома; n — соотношение заряда ядра к заряду электрона (в нашем случае n = 2); с отрицательным знаком указаны слагаемые, вызывающие отталкивание, а с положительным — вызывающие притягивание.
Нормируем L1 к расстоянию между ядром и электроном внутри «атома» R с помощью коэффициента d: L1 = d · R. Теперь можно вынести R за скобки и вместо двух величин (L1 и R) оперировать лишь одной — их соотношением d. В результате переходим к формуле вида
Fe1 = k · (qe / R)2 · (–1 / d2 + n / (d + 1)2 – 1 / (d + 2)2) (2).
С учётом величины и знака заряда аналогично можно вычислить силу воздействия на ядро Fn и на второй (дальний) электрон Fe2:
Fn = k · (qe / R)2 · (n / (d + 1)2 – n2 / (d + 2)2 + n / (d + 3)2) (3),
Fe2 = k · (qe / R)2 · (–1 / (d + 2)2 + n / (d + 3)2 – 1 / (d + 4)2) (4).
Отсюда общая сила воздействия на соседний «атом» F будет равна
F = Fe1 + Fn + Fe2 = k · (qe / R)2 · (–1 / d2 + 2 · n / (d + 1)2 – (n2 + 2) / (d + 2)2 + 2 · n / (d + 3)2 – 1 / (d + 4)2) (5).
Назовём коэффициент, определяемый скобками в конце формулы, в которых учитывается влияние относительного расстояния d, коэффициентом дистанционного взаимодействия атомов (или молекул), и для удобства записи обозначим его греческой буквой «дзета» ζ:
F = k · (qe / R)2 · ζ (6),
где
ζ = –1 / d2 + 2 · n / (d + 1)2 – (n2 + 2) / (d + 2)2 + 2 · n / (d + 3)2 – 1 / (d + 4)2 (7),
а с учётом того, что n = 2, получаем
ζ = –1 / d2 + 4 / (d + 1)2 – 6 / (d + 2)2 + 4 / (d + 3)2 – 1 / (d + 4)2 (8).
Особо подчеркну, что R в формуле (6) — это характеристический размер атома, расстояние между центрами зарядов его частиц, и оно никак не зависит от межатомного расстояния. Межатомное расстояние полностью «спрятано» в параметре d, то есть в коэффициенте дистанционного взаимодействия ζ. Теперь можно вычислить величину и направление силы и попытаться определить, по какому закону она изменяется. Составим таблицу на основании формулы (8).
| d, раз |
1 |
2 |
5 |
10 |
20 |
50 |
100 |
200 |
500 |
1000 |
2000 |
| ζ |
–0.4567 |
–0.0483 |
–0.0012 |
–4.2·10–5 |
–1.1·10–6 |
–6.1·10–9 |
–1.1·10–10 |
–1.8·10–12 |
–7.5·10–15 |
–1.2·10–16 |
–1.9·10–18 |
| отношение ζ к f = –d–6 |
0.45667 |
3.09333 |
18.4929 |
42.2172 |
68.7276 |
95.0837 |
106.628 |
113.065 |
117.163 |
118.571 |
119.283 |
Прежде всего, из таблицы видно, что наши «атомы» всегда испытывают взаимное отталкивание, поскольку коэффициент дистанционного взаимодействия ζ всегда имеет отрицательный знак. Теперь проанализируем не менее важный, но гораздо более тонкий момент — характер изменения этой силы с ростом относительного расстояния между «атомами».
Сначала зависимость силы отталкивания от расстояния между «атомами» более плавная, однако затем становится более крутой и начиная с d > 100, ведёт себя практически обратно пропорционально 6-й степени d. В диапазоне d от 100 до 10000 характер зависимости совпадает с указанной функцией с точностью до нескольких процентов (выделено светло-зелёным в нижней строке таблицы, коэффициент отношения этих функций стремится к –120), проанализировать бóльшие значения d не позволила стандартная точность представления чисел в компьютере, но я не вижу причин, по которым характер зависимости там должен измениться, к тому же значения силы на таких расстояниях пренебрежимо малы и в реальных условиях их можно считать намного меньше влияния всевозможных других внешних факторов.
Рассмотрим ещё одно положение с параллельными друг другу осями обоих «атомов», только в этом случае их оси перпендикулярны связывающей «атомы» прямой.
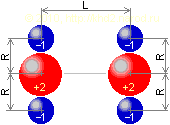 Ещё один вариант параллельной ориентации осей «атомов».
Опуская подробности, приведу сразу конечный полином для коэффициента дистанционного взаимодействия в данном случае:
ζ = –6 / d2 + 8 / (d2 + 1) – 2 / (d2 + 4) (9).
Эта конфигурация с параллельной ориентацией осей распределения зарядов также вызывает силу отталкивания. Причём на близких расстояниях эта сила больше, чем тогда, когда все оси зарядов размещались на одной прямой, зато и убывает она с ростом расстояния заметно скорее, хотя, опять же, обратно пропорционально 6-й степени этого расстояния (коэффициент пропорциональности в данном случае не –120, а –24)...
Из рассмотренного выше можно сделать вывод о том, что и для других расположений атомов эффект будет аналогичным, лишь коэффициенты при членах полинома будут другие. Чуть ниже мы увидим, что это не совсем так. Однако в любом случае можно сказать о том, что если электроны будут вращаться вокруг ядра, то сила отталкивания будет периодически изменяться в соответствии с текущим положением электронов.
Логично предположить, что давление полученного нами «газа» определяется этой силой отталкивания (по крайней мере в нашем случае это именно так). Эта же сила обеспечивает другое свойство газа — стремление заполнить весь доступный ему объём.
Посмотрим, что будет, если мы изменим плотность размещения «атомов», то есть расстояние между ними. Сила взаимодействия при этом изменится обратно пропорционально 6-й степени относительно изменения расстояния: F ~ d–6. А как изменится давление газа на стенку, учитывая, что при равномерном распределении число частиц, приходящихся на единицу площади стенки, изменяется обратно пропорционально квадрату изменения расстояния между ними: N ~ d–2? Очевидно, что давление будет пропорционально количеству «атомов», воздействующих на единицу площади и пропорционально силе воздействия каждого из них, то есть давление изменится по закону
P ~ d–2 · d–6 = d–8 = 1 / d8 (10).
Соответствует ли полученный результат реальности? Нет, не соответствует. Как известно ещё со школы, состояние газа при нормальных условиях достаточно точно описывается уравнением Менделеева-Клапейрона (оно же закон состояния идеального газа), которое для частного случая неизменной температуры и количества вещества принимает вид
P · V = const или P ~ 1 / V (11).
Однако у нас получается, что давление должно меняться обратно пропорционально 8-й степени от расстояния между «атомами», а объём — лишь пропорционально 3-й степени этого параметра, и потому их произведение и близко не может быть константой! В чём же дело?
Электродинамический подход
Попробуем вспомнить, что реальные атомы являются не электростатическими, а электродинамическими образованиями и обладают магнитными свойствами, в том числе собственным магнитным моментом. Как поведут себя свободные магниты, будучи предоставлены сами себе на достаточно близком расстоянии друг от друга? Они развернутся друг к другу разноимёнными полюсами и начнут притягиваться! Какова эта сила притяжения?
Как известно, на заряд, движущийся в электромагнитном поле, действует сила Лоренца, вычисляемая по формуле
F = q · (E + [v × B]) (12),
где надчёркивание означает векторный характер величины; q — величина заряда; E — векторная напряжённость электрического поля; v — векторная скорость заряда; B — векторная напряжённость магнитного поля; символ « ×» означает векторное произведение величин, заключённых в квадратные скобки.
В то же время в соответствии с уравнениями Максвелла движущийся заряд создаёт электрическое поле напряжённостью
E = (q / (4 · π · ε · ε0)) · (r / r3) · (1 – v2 / c2) / (1 – [n × v]2 / c2)3/2 = (n · q / (4 · π · ε · ε0 · r2)) · (1 – v2 / c2) / (1 – [n × v]2 / c2)3/2 (13),
и магнитную индукцию
B = (ε · μ / c2) · [v × E] (14),
где в дополнение к обозначениям формулы (12) r — вектор от заряда к точке измерения напряжённости поля, r — модуль, т.е. длина этого вектора (расстояние между точкой измерения и зарядом); n — единичный вектор, равный отношению r / r; ε и ε0 — относительная диэлектрическая проницаемость и диэлектрическая проницаемость вакуума; μ — магнитная проницаемость; c — скорость распространения электромагнитных возмущений в вакууме (скорость света). [n × v]2 равно квадрату длины проекции вектора v на плоскость, перпендикулярную единичному вектору n.
На расстояниях, сравнимых с размерами атома (~10–10 м), официальная физика считает допустимым применение такого подхода, поскольку эти расстояния на пару порядков превышают комптоновскую длину волны электрона (~4·10–13 м), где такой подход считается уже неприменимым.
Тем не менее, формула (14) однозначно показывает линейную связь абсолютных величин напряжённости электрического поля и магнитной индукции при условии слабо изменяющихся скоростей. Поэтому и учёт электродинамического взаимодействия в конечном итоге даст для коэффициента дистанционного взаимодействия ζ выражение, аналогичное формулам (7), (8) и (9), то есть опять изменение силы взаимодействия на больших расстояниях будет обратно пропорционально 6-й степени изменения расстояния между атомами. Почему же в законе состояния идеального газа фигурируют совсем другие закономерности?
Взаимное притяжение
Похоже, дело заключается в том, что взаимодействие между атомами, имеющими неравномерное распределение внешних зарядов, происходит гораздо сложнее и его нельзя свести лишь к рассмотренным выше ситуациям, экстраполируя их поведение и на все промежуточные случаи. В самом деле, будучи предоставлены сами себе, в силу общего принципа минимизации суммарной энергии системы наши «атомы» постараются занять положение с минимальной потенциальной энергией, а для этого они должны сориентироваться разноимёнными неоднородностями зарядов друг к другу, — таким образом, чтобы испытывать наибольшее взаимное притяжение (или хотя бы наименьшее взаимное отталкивание). При этом рассмотренные выше «атомы» должны принять примерно такое положение, как показано на этом рисунке:
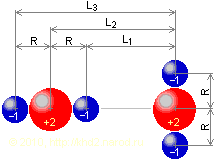 Энергетически оптимальная ориентация «атомов» с неоднородностями внешнего распределения зарядов.
Для краткости назовём это положение «перпендикулярным», а обсуждаемое в предыдущих пунктах, когда центры всех зарядов каждого из «атомов» были расположены на параллельных прямых или вообще на одной и той же прямой — «параллельным».
В этом случае коэффициент дистанционного воздействия для компонентов правого «атома» (начиная с верхнего электрона) с учётом величины и знака зарядов будет вычисляться как
ζe1 r = –1 / (d2 + 1) + 2 / ((d + 1)2 + 1) – 1 / ((d + 2)2 + 1) (15),
ζn r = 2 / d2 – 2 · 2 / (d + 1)2 + 2 / (d + 2)2 (16),
ζe2 r = –1 / (d2 + 1) + 2 / ((d + 1)2 + 1) – 1 / ((d + 2)2 + 1) (17).
Для компонентов левого атома (начиная с левого электрона) эти же коэффициенты будут определяться формулами
ζe1 l = –1 / ((d + 2)2 + 1) + 2 / (d + 2)2 – 1 / ((d + 2)2 + 1) (18),
ζn l = 2 / ((d + 1)2 + 1) – 2 · 2 / (d + 1)2 + 2 / ((d + 1)2 + 1) (19),
ζe2 l = –1 / (d2 + 1) + 2 / d2 – 1 / (d2 + 1) (20).
Как и следовало ожидать, в сумме оба набора формул содержат одни и те же члены, хотя и размещённые в разном порядке — ведь по третьему закону Ньютона воздействие правого «атома» на левый должно быть в точности таким же, как и левого на правый. Сводя воедино любой из наборов (15)-(17) или (18)-(20), получим весьма громоздкую формулу для коэффициента дистанционного взаимодействия наших «атомов» при перпендикулярной взаимной ориентации:
ζ = 2 / d2 – 2 / (d2 + 1) – 4 / (d + 1)2 + 4 / ((d + 1)2 + 1) + 2 / (d + 2)2 – 2 / ((d + 2)2 + 1) (21).
Составим для формулы (21) такую же таблицу, как и для формулы, описывающей параллельное расположение зарядов (8).
| d, раз |
1 |
2 |
5 |
10 |
20 |
50 |
100 |
200 |
500 |
1000 |
2000 |
| ζ |
0.8222 |
0.0629 |
8.9·10–4 |
2.3·10–5 |
4.7·10–7 |
2.3·10–9 |
3.8·10–11 |
6.1·10–13 |
2.5·10–15 |
4.0·10–17 |
6.2·10–19 |
| отношение ζ к f = d–6 |
0.82222 |
4.02614 |
13.9101 |
22.8293 |
29.9433 |
35.5380 |
37.6870 |
38.8221 |
39.5236 |
39.7606 |
39.8919 |
| ζ(8) + ζ(21) |
0.3656 |
0.0146 |
–2.9·10–4 |
–1.9·10–5 |
–6.1·10–7 |
–3.8·10–9 |
–6.9·10–11 |
–1.2·10–13 |
–5.0·10–15 |
–7.9·10–17 |
–1.2·10–18 |
Как и в предыдущих случаях, при d > 100 зависимость становится обратно пропорциональной 6-й степени расстояния (с коэффициентом 40), а при d < 0.2 она пропорциональна 2-й степени расстояния, т.е. тогда закон Кулона для двух ближайших зарядов соседних атомов действует намного сильнее влияния всех прочих зарядов.
Однако здесь мы имеем одно принципиальное отличие от результатов формул (8) и (9): все результаты положительны, то есть атомы с таким взаимным расположением притягиваются! Поэтому в конце таблицы была добавлена ещё одна строка, показывающая сумму коэффициентов дистанционного взаимодействия для параллельной (8) и перпендикулярной (21) ориентации атомов. В ней наглядно видно, что когда расстояние превышает 3 радиуса, притяжение сменяется отталкиванием. Впрочем, такое суммирование имеет лишь познавательный аспект, а вот физического смысла не имеет — ведь одна и та же пара атомов не может одновременно находиться в двух разных положениях... Зато наглядно видно, что с ростом расстояния притяжение даже в наиболее выгодной конфигурации ослабевает быстрее, чем отталкивание. С другой стороны, сила отталкивания в случае, когда оси зарядов параллельны друг другу, но перпендикулярны связывающей их прямой, на близких расстояниях ещё сильнее, но и убывает с ростом расстояния скорее. Отметим эти обстоятельства — они могут оказаться весьма важными.
И притяжение, и отталкивание
Теперь было бы логично рассмотреть «атомы», конфигурация зарядов в которых обеспечивает одновременно и притяжение, и отталкивание. Сначала рассмотрим простейший случай, когда атом содержит две взаимно перпендикулярные пары «электронов».
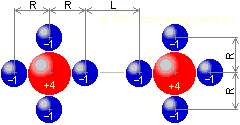 Одновременное притяжение и отталкивание.
Для компенсации зарядов возросшего числа «электронов» заряд ядра таких «атомов» должен быть увеличен до +4. С учётом этого обстоятельства по аналогии с выводом формул (8), (9) и (21) получаем полином для расчёта коэффициента дистанционного взаимодействия:
ζ = –1 / d2 + 8 / (d + 1)2 – 4 / ((d + 1)2 + 1) – 20 / (d + 2)2 + 16 / ((d + 2)2 + 1) – 2 / ((d + 2)2 + 4) + 8 / (d + 3)2 – 4 / ((d + 3)2 + 1) – 1 / (d + 4)2 (22).
Составляем уже привычную таблицу на основании формулы (22).
| d, раз |
1 |
2 |
5 |
10 |
20 |
50 |
100 |
200 |
500 |
1000 |
2000 |
| ζ |
–0.3514 |
–0.0316 |
–6.7·10–4 |
–2.3·10–5 |
–5.8·10–7 |
–3.3·10–9 |
–5.7·10–11 |
–9.4·10–13 |
–4.0·10–15 |
–6.3·10–17 |
–9.9·10–19 |
| отношение ζ к f = –d–6 |
0.35136 |
2.01975 |
10.4553 |
22.9321 |
36.8478 |
50.7584 |
56.8821 |
60.3049 |
62.4878 |
63.2378 |
63.2793 |
В данном случае коэффициент дистанционного взаимодействия становится обратно пропорциональным 6-й степени расстояния несколько позже, чем в рассмотренных ранее конфигурациях с 2-мя электронами (коэффициент пропорциональности стремится к –64). Кроме того, тут сила взаимодействия всегда является силой отталкивания. Но это и не удивительно, ведь для данной конфигурации «атомов» энергетически оптимальным будет другое взаиморасположение.
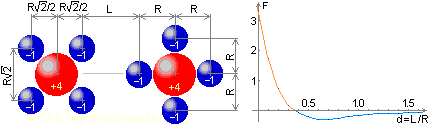 Энергетически оптимальное взаиморасположение «атомов», имеющих по 4 «электрона». Справа показан график изменения силы взаимодействия F в зависимости от относительного расстояния d = L / R.
Здесь формула для коэффициента дистанционного взаимодействия окончательно теряет все шансы на адекватное восприятие в аналитической форме даже при том, что я заменял (√2 / 2)2 на 0.5:
ζ = –2 / (d2 + 0.5) + 4 / (d + √2 / 2)2 – 2 / ((d + 1)2 + (1 – √2 / 2)2) + 8 / ((d + 1)2 + 0.5) – 2 / ((d + √2)2 + 0.5) – 2 / ((d + 1)2 + (1 + √2 / 2)2) + 8 / ((d + 1 + √2 / 2)2 + 1) – 16 / (d + 1 + √2 / 2)2 + 8 / ((d + 1 + √2 / 2)2 + 0.5) – 2 / ((d + 1 + √2 / 2)2 + (1 – √2 / 2)2) – 2 / ((d + 1 + √2 / 2)2 + (1 + √2 / 2)2) – 2 / ((d + 2)2 + 0.5) + 4 / (d + 2 + √2 / 2)2 – 2 / ((d + 2 + √2)2 + 0.5) (23).
И если я нигде не ошибся во всей этой алгебраической абракадабре, то в таблице окажутся следующие значения.
| d, раз |
0.1 |
0.2 |
0.5 |
1 |
2 |
5 |
10 |
20 |
50 |
100 |
200 |
| ζ |
1.7174 |
0.7411 |
–0.2109 |
–0.1695 |
–0.0296 |
–7.7·10–4 |
–2.6·10–5 |
–6.2·10–7 |
–3.4·10–9 |
–5.8·10–11 |
–9.5·10–13 |
| отношение ζ к f = d–6 |
1.7·10–6 |
4.7·10–5 |
–0.0033 |
–0.1695 |
–1.8939 |
–11.975 |
–25.650 |
–39.522 |
–52.412 |
–57.844 |
–60.824 |
Теперь на близких расстояниях (d ≤ 0.361, в таблице выделено красноватым фоном) действует сила притяжения, которая на более далёких сменяется силой отталкивания, хотя отталкивание здесь всегда меньше, чем в предыдущем случае одинаковой ориентации «атомов». На больших дистанциях зависимость снова обратно пропорциональна 6-й степени расстояния с коэффициентом пропорциональности, стремящимся к –64, однако в области малых дистанций она так и не становится квадратичной.
На графике, построенном по более подробным результатам для диапазона d от 0 до 1.6 хорошо видно, что после сближения «атомов» на расстояние менее критического (чуть менее 0.4) отталкивание сменяется притяжением, которое резко нарастает при дальнейшем сближении — такие «атомы» слипнутся в весьма прочную «молекулу». Кстати, теоретически d может быть и меньше нуля (но не меньше –1), когда «атомы» сближаются так, что электрон одного из них попадает в зону «электронной оболочки» другого.
Можно найти и другие взаимные расположения этих атомов, при которых на близких расстояниях они будут испытывать взаимное притяжение, с ростом расстояния сменяющееся отталкиванием. Например, это смещение одного атома относительно другого при параллельной ориентации осей расположения зарядов, показанное ниже. Расчёт я не привожу, поскольку он не менее громоздок, чем только что выполненный.
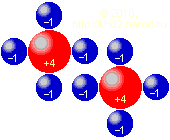 Ещё одно расположение с возможным взаимным притяжением на близких расстояниях. Характер взаимодействия аналогичен предыдущему случаю.
Подобное поведение уже более похоже как на то, что наблюдалось в проведённых виртуальных экспериментах с электростатической моделью взаимодействия, так и на то, что можно наблюдать в реальной жизни. Однако и здесь учтены ещё не все нюансы.
Взаимодействие множества свободных объектов с неравномерным распределением зарядов
Взаимная ориентация
Как мы только что выяснили, для рассмотренных примеров простейших электрически нейтральных симметричных комбинаций пространственно разнесённых зарядов взаимно параллельная ориентация осей неоднородностей зарядов объектов обычно вызывает их отталкивание независимо от угла между этими осями и прямой, связывающей центры объектов. И наоборот, максимально непараллельная ориентация осей неоднородностей вызывает уменьшение отталкивания и даже возникновение притяжения объектов друг к другу, причём притяжение вблизи может сменяться отталкиванием по мере роста расстояния между объектами.
С учётом того, что обычно количество взаимодействующих объектов (молекул или атомов) намного превышает 2, да ещё всё это происходит не на плоскости, а в трёхмерном пространстве, можно уверенно утверждать, что в любой момент времени один и тот же объект (атом или молекула) по отношению к разным соседям находится в различных ориентациях, способствующих как взаимному притягиванию, так и взаимному отталкиванию.
Из общеизвестных законов дистанционного взаимодействия, как электромагнитного, так и гравитационного, следует, что в физическом множестве одинаковых объектов из всех взаимодействий одного объекта с другими наибольшей потенциальной энергией обладает взаимодействие с ближайшими соседями, и прежде всего, с самым ближайшим из них. На минимальную энергию взаимодействия с ближайшим соседом объект и будет ориентироваться, стремясь развернуться таким образом, чтобы взаимная неравномерность распределения зарядов обеспечила бы наибольшую силу притяжения (или наименьшую силу отталкивания, что по сути то же самое). Ко всем остальным объектам ориентация будет уже по принципу «как получится», что с гораздо большей степенью вероятности приведёт к их взаимному отталкиванию, чем к притяжению, хотя сила этого взаимодействия, естественно, будет намного меньше, чем с ближайшим соседом, под который подстраивается рассматриваемый нами объект.
Впрочем, если в непосредственной близости есть и другие объекты, «наш» объект может «учесть их интересы», заняв пропорционально их силе воздействия некое промежуточное положение между между ориентациями, оптимальными для каждого из ближайших соседей. Если же сила воздействия нескольких соседей равна, то объект может попасть в положение буриданова осла, и его ориентация будет неоптимальной до тех пор, пока в силу различных внешних факторов среди «кандидатов в лидеры» не определится явный фаворит.
Изменение распределения зарядов
Но и это ещё не всё. Если элементы объекта не имеют жёсткой связи друг с другом (например, валентные электроны атомов), то под воздействием поля соседей они неизбежно отклонятся от своих «идеальных» мест, которые они занимали бы в отсутствие каких бы то ни было внешних воздействий. Подобные перемещения элементов становятся очевидными при достаточно тесном сближении объектов. Скажем, в случае сильного сближения наших «атомов» электроны одного атома будут как бы «расталкивать» ближние к ним электроны другого атома, оголяя ближайший к ним участок его ядра и тем самым увеличивая силу взаимного притяжения «атомов» по сравнению с рассчитанной для жёсткой конструкции с неизменной геометрией. При этом взаимное расположение электронов автоматически приобретает конфигурацию, оптимальную для притяжения «атомов» друг к другу.
Как мы уже видели выше на нескольких примерах, изменение конфигурации зарядов внутри объекта оказывает существенное влияние на коэффициент его дистанционного взаимодействия с соседями — вплоть до того, что притяжение может смениться отталкиванием или наоборот. Причём на расположение элементарных зарядов влияет не только текущее распределение поля сил, но и такие механические характеристики материальных носителей зарядов, как их текущая скорость и масса (как мера инерционности). Учесть всё это в общей аналитической форме, пригодной для практического точного расчёта, не представляется возможным.
Хочу предостеречь от пренебрежения этим фактором, хотя иногда он может показаться малозначащим. Даже небольшое перераспределение зарядов вызывает поляризацию прежде симметричного объекта, а это, в свою очередь, вызывает его переориентацию либо, наоборот, стабилизацию ориентации относительно своих соседей. Более того, при моделировании взаимодействия именно переразмещение зарядов либо невозможность такого переразмещения обуславливают как количество «атомов» в молекулах, так и геометрическую форму этих «молекул». То же самое наблюдается и в реальном мире, наиболее наглядно проявляясь в кристаллических решётках разных типов. Наконец, это переразмещение является главной причиной некоторых физических эффектов. Именно подобным смещением зарядов классическая физика объясняет, например, поляризацию диэлектриков во внешнем электрическом поле.
Моделирование взаимодействия
Мы убедились, что огромное число разнообразных факторов, которое необходимо учесть для точного расчёта взаимного влияния объектов с неравномерным распределением зарядов, к каковым можно отнести атомы и молекулы, делает невозможным расчёт их поведения в аналитической форме, пригодной для разумного использования. Для прикидок на бумаге есть только один оправданный способ, который термодинамика использует уже не первую сотню лет — рассматривать их совокупность как некую среду, обладающую усреднёнными характеристиками и пытаться подобрать эмпирические закономерности, описывающие взаимосвязь этих усреднённых характеристик.
Именно это мы и наблюдаем в современной термодинамике, которую более точно именуют «феноменологической термодинамикой», подчёркивая, что она описывает внешние проявления процессов, не связывая их с глубинной сутью этих явлений. В результате неизбежно появление многочисленных поправок, ограничений и всевозможных условий применимости, на которые так богата классическая термодинамика. Тем не менее, до определённой степени этот подход имеет право на жизнь, более того, он оправдан и практичен, о чём свидетельствует многолетняя история термодинамики. Правда, при одном условии — если не возводить эти эмпирические закономерности в абсолют и чётко сознавать условия их применимости.
С другой стороны, мы только что убедились, что многие происходящие в реальности явления успешно моделируются при помощи компьютера на основе одной, максимум двух-трёх простых и ясных закономерностей, таких как закон Кулона для электростатической модели или сила Лоренца вкупе с уравнениями Максвелла для движущегося заряда в случае электродинамической модели. Правда, эти закономерности применяются к каждому взаимодействию между объектами, и потому в силу огромного результирующего объёма вычислений выполнить за разумное время расчёт хотя бы для десятка-другого объектов можно лишь при использовании компьютера. Выше мы видели, что на качественном уровне различия между электростатическим и электродинамическим подходами невелики, — именно поэтому я ограничился электростатической моделью.
К сожалению, возможности моделирования на персональных компьютерах ограничены несколькими сотнями или, в лучшем случае, несколькими тысячами взаимодействующих объектов. Даже в случае использования распределённых вычислений на современных мощных компьютерных кластерах разумный максимум я оцениваю в сотню тысяч объектов одновременно (это 105). Для сравнения, лишь в одном кубическом сантиметре воздуха при нормальных условиях находится более 1019 молекул, а в одном литре воды — 6·1026. Дело в том, что с ростом числа взаимодействующих зарядов объём вычислений возрастает в квадратичной зависмости — ведь необходимо учесть взаимодействие каждого элементарного объекта с каждым. Оптимизация алгоритмов позволяет лишь немного снизить наклон этой зависимости, но не решить проблему в принципе. Более же серьёзные сокращения объёма вычислений, связанные с различными упрощениями и допущениями модели взаимодействия, как показала практика, приводят к принципиальным искажениям результатов, даже если на первый взгляд отступления от исходного «тупого» расчёта минимальны. И хотя расчёт легко можно распараллелить, это не даст кардинального выигрыша в количестве одновременно участвующих в расчёте элементарных объектов при условии сохранения разумного времени выполнения такого расчёта.
Очевидно, что по этим причинам использовать компьютерное моделирование на столь глубоком уровне для инженерных применений в настоящее время вряд ли возможно. Однако такие модели позволяют наглядно наблюдать происходящие процессы и могут подсказать решения, абсолютно невозможные в рамках знаний, полученных феноменологическим путём.
Некоторые выводы о взаимодействии свободных объектов с неравномерным распределением зарядов
Подводя итог вышеизложенному, можно со всей определённостью утверждать, что такие свойства газа, как его внутреннее давление и стремление заполнить весь отведённый ему объём, обусловлены не только, и даже не столько «скоростью частиц» и «частотой соударений», на что намекают адепты молекулярно-кинетической теории, а именно электростатическим взаимодействием его частиц (для реальных атомов электродинамическим, но действующим по аналогичным закономерностям). Но нельзя не отметить и логичность механистического подхода. Дело в том, что по этой теории газ рассматривается как совокупность электрически нейтральных частиц, испытывающих лишь механическое взаимодействие друг с другом непосредственно в момент столкновения в виде «абсолютно упругого соударения». В рамках таких представлений трудно не придти к заключению, что температура — это мера кинетической энергии частичек газа, а давление обусловлено передачей импульсов ударяющихся о стенки частичек, т.е. пропорционально их скорости и количеству ударов на единицу поверхности.
Так что ошибка лежит не в формальной логике, а в самой механистичности традиционной молекулярно-кинетической теории. При рассмотрении частиц газа (атомов и молекул) как электрически нейтральных совокупностей разнесённых в пространстве зарядов, появляется другой механизм возникновения давления — электрический (электростатический в моей компьютерной модели и электродинамический в реальности; оба действуют по схожим закономерностям). Подобный подход делает необязательным прямые столкновения частиц газа, более того, в большинстве случаев такие столкновения исключаются из-за дистанционного электрического взаимодействия, хотя, поскольку сила такого взаимодействия возрастает обратно пропорционально квадрату расстояния между объектами, оно в наибольшей степени проявляется лишь при существенном сближении частиц, и потому при рассмотрении ситуации «в общем» траектории таких взаимодействий будут весьма похожи как раз на те самые «абсолютно упругие механические столкновения частиц», которые постулированы в рамках молекулярно-кинетической теории...
Но это лишь одна сторона медали. Другая сторона заключается в том, что дистанционное электрическое взаимодействие частиц неизбежно приводит к некоторой степени согласованности их движения и ориентации в пространстве, так что о хаотичности скоростей и положения в пространстве в её классическом толковании здесь речь уже не идёт, что наглядно показывают результаты компьютерного моделирования.
Следствия из электрической природы взаимодействия частиц газа
Принятие не механического, а электрического подхода к взаимодействию частиц газа ведёт к нескольким важным следствиям, кардинально отличным от традиционных представлений.
-
Электрический характер взаимодействия частиц (атомов и молекул) обуславливает как их взаимное отталкивание, приводящее к возникновению давления газа, так и их взаимное притяжение, приводящее к возникновению молекул. При этом возможные конфигурации и размеры молекул определяются конфигурацией распределения зарядов в атомах и их переконфигурацией при объединении атомов в молекулы.
-
Дистанционный характер электрического взаимодействия обуславливает отсутствие необходимости механических столкновений частиц газа для обеспечения из разлёта и заполнения всего отведённого объёма, а также поддержания давления газа, оказываемого им на стенки ограничивающего его сосуда и погружённые в газ твёрдые и жидкие тела.
-
Неравномерное распределение зарядов внутри каждой частицы среды обеспечивает одновременно ее взаимное отталкивание с одними соседями и притяжение или меньшее отталкивание с другими соседями. При этом определяющим фактором для выбора ориентации той или иной частицы является минимальная потенциальная энергия взаимодействия с ближайшим соседом, обеспечивающая их наибольшее взаимное притяжение. В случае отталкивания приоритет отдаётся положению с наименьшим взаимным отталкиванием, но в любом варианте существенные поправки может внести и взаимодействие с другими частицами среды, прежде всего находящимися вблизи рассматриваемой.
-
С ростом расстояния и сила притяжения, и сила отталкивания убывают, однако в среднем сила притяжения убывает быстрее, чем сила отталкивания, поэтому на больших расстояниях преобладает отталкивающее взаимодействие.
-
Дистанционный характер взаимодействия с преобладающим отталкиванием наряду с разлётом газа по всему объёму и поддержанием его давления приводит к тому, что частицы газа склонны не к хаотическому стремительному перемещению по всему выделенному для газа объёму, а к пребыванию в более-менее ограниченной части пространства, называемой «глобулой». Доступ других частиц во внутреннее пространство глобулы возможен, но затруднён из-за отталкивающего воздействия хозяина глобулы. Вместе с тем глобула не фиксируется в определённом участке пространства, а может относительно медленно дрейфовать по всему выделенному для газа объёму, как правило вместе со своими ближайшими соседями. Характер блуждания частиц приближается к хаотическому лишь при их низких концентрациях, когда взаимодействие весьма мало из-за больших расстояний между ними, то есть при высоком разрежении.
-
Сложный характер взаимодействия, обусловленный как геометрией распределения зарядов внутри частиц, так и взаимным расположением самих частиц в пространстве, приводит к существенному отличию зависимости силы этого взаимодействия от расстояния по сравнению с обратноквадратичной, характерной для «лабораторного» взаимодействия одиночных зарядов.
-
Наконец, в общем случае характер взаимодействия определяется особенностями распределения зарядов в частицах и потому может различаться для различных газов. С ростом расстояния между частицами (т.е. при разрежении газа) влияние этих особенностей уменьшается и различия между поведением газов разного состава постепенно исчезают.
О зависимости силы взаимодействия от расстояния
Как уже отмечалось выше, уравнение состояния идеального газа утверждает факт обратно-линейной зависимости давления и объёма при постоянных температуре и количестве вещества. Эта зависимость хорошо подтверждается экспериментально в условиях, близких к нормальным. Давление равно усреднённой силе воздействия одной молекулы на единицу ограничивающей поверхности, умноженной на количество молекул, контактирующих с этой самой единицей поверхности. В проведённых виртуальных экспериментах концентрация частиц была более-менее равномерной, и нет оснований предполагать, что в реальности дело обстоит иначе. С учётом этой равномерности можно утверждать, что количество частиц на единицу площади поверхности обратно пропорционально квадрату расстояния между ними, и усреднённая сила их взаимодействия должна меняться обратно пропорционально первой степени растояния, то есть по линейному закону. Однако полученные нами выше зависимости показывают совсем другой характер — они обратно пропорциональны более высоким степеням (от 2-й до 6-й). В чём же дело?
Линейная зависимость силы взаимодействия от расстояния
Можно предположить, что дело заключается именно в сложном характере взаимодействия множества частиц газа между собой, обусловленном суммированием сил отталкивания и притяжения с ближайшими и более отдалёнными соседями, в установившихся условиях находящимися в состоянии динамически поддерживаемого статистического равновесия. Тем не менее, явных причин для именно линейного характера зависимости силы взаимодействия от объёма на данный момент в рамках изложенного выше механизма я не вижу. Их и на самом деле нет! Поэтому можно было бы считать это просто совпадекнием, своего рода «шуткой природы».
В действительности этот факт имеет более глубокие причины, нежели простое совпадение. Просто в газах при относительно небольших концентрациях частиц преобладает кинетический механизм давления, успешно рассматриваемый в рамках классической МКТ. Кстати, при деформации твёрдых тел возникающая сила также линейно зависит от изменения размеров как при сжатии, так и при растяжении (классический закон Гука: F = k · Δ l / l, где k — коэффициент упругости, индивидуальный для каждого материала), но там причины совсем другие, хотя в этом случае преимущественное изменение размеров происходит только по одной оси, то есть изменения линейного размера и объёма вещества оказываются очень близки и естественным образом отождествляются — вот пример феноменологической мимикрии разных процессов, провоцирующей попытки поиска единого объяснения для совершенно различных механизмов! Аналогичная зависимость наблюдается и в жидкостях, где коэффициент сжимаемости β измеряется в единицах, обратных единицам давления (применяется для относительного изменения объёма).
Поправки Ван-дер-Ваальса и других
Когда расстояние между атомами становится меньше, электрофизические механизмы начинают вносить заметный вклад в давление газа на стенки сосуда. Как известно, для больших давлений (обычно начиная с 10 атм) в традиционной термодинамике начинают вводиться различные поправки, а классическое «PV=const» превращается в гораздо более сложное и нелинейное выражение. Существует множество вариантов этих поправок, среди которых наиболее часто используется уравнение Ван-дер-Ваальса: (V – n · b) · (P + n2 · a2 / V2) = n · R · T.
Поправки, входящие в это уравнение, индивидуальны для каждого типа газа, как и должно быть в соответствии с последним из полученных нами следствий. Причина, по которой возникает необходимость вводить эти поправки, обычно объясняется «взаимным притяжением молекул газа, возникающим на близком расстоянии». Принято считать, что в нормальных условиях при давлении 1 атм расстояние между молекулами равно примерно 100 их газокинетическим диаметрам, близким к их реальным размерам (соответствует d = 200 в нашем расчёте). В этом случае при 10 атм d уменьшится в 3√10 ~ 2.15 раза и составит примерно 90, что хорошо совпадает с началом изменения характера зависимостей, полученным в результате расчётов взаимодействия частиц с пространственно разнесёнными зарядами, но вот это как раз случайность. Зато квадрат объёма в знаменателе (в скобках вместе с давлением) не случаен — он соответствует межмолекулярному расстоянию в степени –6 и соответствует потенциальной электрофизической составляющей давления.
Как мы убедились выше, действительно, при уменьшении расстояния между частицами сила их отталкивания может смениться притяжением. Более того, на очень близких расстояниях, где взаимодействие ближайших друг к другу компонентов соседних атомов намного превышает взаимодействие всех других зарядов, входящих в состав этих атомов, такое притяжение может стать достаточно большим для того, чтобы удерживать атомы вместе, образуя твёрдое состояния вещества. На ещё более близких растояниях взаимодействие становится ещё сильнее, в результате образуются молекулы, обладающие ещё большей внутренней устойчивостью по сравнению с объединяющими их кристаллами. Правда, в одном Ван-дер-Ваальс ошибался — ни в жидкости, ни в газе межмолекулярного притяжения нет, оно существует только в твёрдых телах.
Тем не менее, уравнение Ван-дер-Ваальса отнюдь не универсально и имеет очень существенные ограничения, поэтому наряду с ним используются и другие варианты поправок, среди которых наиболее популярны уравнения Дитеричи и Бертло. Впрочем, они также не идеальны. На данный момент не удалось достаточно адекватно описать поведение газов в широком диапазоне условий с помощью уравнения менее чем с 5-ю постоянными, индивидуальными для конкретного газа. Всё это подтверждает сделанный вывод о крайней сложности расчёта протекающих процессов и принципиальной невозможности свести их описание на макроуровне к единой достаточно простой аналитической формуле.
Отступление от темы
Не надо думать, что вышеизложенным я открыл Америку. Попытки найти электрический механизм взаимодействия частиц газа многократно и целенаправлено предпринимались с тех самых пор, как были проведены первые эксперименты, показавшие электрическую природу составляющих атома, то есть на протяжении многих десятков лет.
Кстати, через некоторое время после того, как я проделал все эти расчёты, у меня появились смутные воспоминания, что нечто подобное я уже слышал давным-давно, ещё на институтских семинарах по физике, как раз когда речь шла о физических свойствах газов. Конечно, говорилось об этом не в рамках официального курса, а факультативно, «для общего развития», под напором особо пытливых студентов (к коим я не относился) и лишь в общих чертах, на уровне концепции, без конкретных чисел и выкладок. И, по ещё более смутным воспоминаниям, развивать данную тему на экзаменах не рекомендовалось — для нашего же блага. Но поскольку тогда этот вопрос был для меня малоактуален и воспринимался не более чем как занимательная информация, всё это успешно затонуло в глубинах памяти...
Почему же всё это так и не получило развития? Потому что в данном случае не удалось вычленить элементарную базовую ситуацию, которую можно было бы описать одной или несколькими простыми аналитическимим формулами — как мы видели, попытки конкретных расчётов даже простейших комбинаций заряженных частиц выливаются в многоэтажные полиномы, результат которых становится обратно пропорциональным 6-й степени расстояния между взаимодействующими частицами, а не 1-й, как это следует из результатов экспериментов. Несмотря на то, что в различных частных случаях эти полиномы дают как отталкивание, так и притяжение, аналитически «усреднить» всё это и получить единую формулу, пригодную для практического использования, не представляется возможным. И лишь появление компьютеров, способных «перемолоть» огромный объём вычислений и прямо смоделировать ситуацию, позволило немного продвинуться в этом вопросе.
Смотреть шире!
Только что был весьма подробно рассмотрен электрический (я специально не употребляю более узкий термин «электростатический») механизм взаимодействия атомов и молекул, с помощью которого можно с некоторым успехом попытаться объяснить все аспекты этого взаимодействия, хотя бы на качественном уровне, подтверждая их результатами компьютерного моделирования. Очень привлекательная идея, и я некоторое время следовал ей с большим энтузиазмом. Опасное заблуждение!
Не следует повторять ошибки предшественников — не стоит пытаться втиснуть все явления в рамки одного-единственного механизма. Жизнь сложнее и многообразнее, и на любой реальный объект одновременно воздействует огромное количество самых различных факторов, вклад которых зависит от множества условий. В данный момент я убеждён, что силы межатомного и межмолекулярного отталкивания имеют несколько механизмов, и на близких межатомных расстояниях преобладает действие рассмотренного выше электрического, но на дальних расстояних он ослабевает слишком быстро, и там основной вклад вносит другой механизм, имеющий как раз линейный характер.
♦
|