Двигатель Клема как тепловая машина
Попробуем рассмотреть двигатель Клема с точки зрения термодинамики, как тепловую машину. Сразу ещё раз оговорюсь, что, если оставаться в рамках классической термодинамики, то теплообменник двигателя Клема должен быть холодным и нагревать рабочую жидкость за счёт тепловой энергии окружающей среды — больше ему взять энергию просто неоткуда. Однако почти все в один голос утверждают, что его теплообменник был горячим и служил для охлаждения. И всё же провести детальный анализ двигателя Клема с точки зрения термодинамики я считаю не просто нужным, а необходимым.
Идея термодинамического подхода привлекательна ещё и тем, что в её рамках (с холодным теплообменником) система из двигателя Клема и нагрузки (включая все потери) является замкнутой, и потому может работать сколь угодно долго без теплообмена со средой вне своих границ! Правда, второй закон термодинамики запрещает существование таких систем...
Я специально не ограничился конечными результатами, а привёл достаточно подробный ход рассуждений с выдвижением нескольких предположений, которые позже были отброшены, а то и заменены прямо противоположными рекомендациями. Это сделано для того, чтобы дать возможность другим не тратить время на самостоятельное изучение этих тупиков, либо, напротив, найти ошибку в моих рассуждениях и пойти дальше правильной дорогой!
Эту идею я рассматривал, лишь увидев «классическую» схему мотора Клема, где конус нарисован вращающимся в воздушной среде, и ещё не зная о предположительном прототипе этого двигателя — асфальтовом насосе — где и входная, и выходная камеры, а также каналы конуса заполнены асфальтом без каких-либо существенных включений воздуха. Прежде всего это относится к выходной камере, куда и нагнетался асфальт — уж там-то даже те пузырьки воздуха, что могли попасть с асфальтовой массой во входную камеру, за счёт высокого давления уменьшались в объёме во много раз. Поэтому ни о каком свободном испарении и расширении пара речи быть не может хотя бы по этой причине. Тем не менее, возможно, что аномально долгое вращение именно этого насоса при отключённом внешнем приводе и заставило Клема заняться своим двигателем. Затем появились сведения и о других эффектах, которые могли лежать в основе работы двигателя Клема. Всё эти новые данные указывают на то, что причина работы мотора Клема кроется отнюдь не в фазовых превращениях рабочего тела, и уж ни в коем случае не в термодинамических аспектах этих процессов! Я не стал существенно удалять или редактировать текст, но внёс дополнения, сделанные позже с учетом этого вывода, которые выделены жирным красноватым шрифтом — таким же, как этот абзац. Не пренебрегайте ими, чтобы не пойти по ложному пути!
Рабочий цикл двигателя Клема
Фазы рабочего цикла двигателя Клема
Форсунки и сопла
Конус — главная деталь
Общая схема переноса тепла в конусе
Уточнённая схема теплообмена в конусе
Замыкая круг
Оценка энергетического баланса
Несколько больших «НО»...
Что говорит закон сохранения энергии?
Что говорит эксперимент?
Что следует из экспериментальных данных?
И всё же...
Предполагаемые режимы работы двигателя Клема
Начало работы
Холостой ход
Повышение нагрузки
Внезапная остановка
Регулировка мощности
Выбор параметров конструкции
Вода, масло, спирт...
Первый расчёт элементов конструкции
Сопло
Конус
Как поддержать давление?
Как увеличить потери?
Гладкая труба
Труба с перегородками
Предварительные итоги
Теперь понятно, почему...
«Размер имеет значение» и другие выводы
Рабочий цикл двигателя Клема
Попытаемся более подробно понять возможные принципы работы этой необычной конструкции, посмотрев на неё, как на тепловую машину.
Прежде всего хочу обратить внимание на один интересный факт. Судя по описанию, в двигателе Клема в качестве рабочего тела используется жидкость, и более того, жидкость при достаточно высокой температуре (порядка 150°С). Очевидно, такая высокая температура выбрана не случайно, ведь если бы этот разогрев не был нужен, ничто не мешало ограничить его более низкой температурой, скажем 80..90°С, стандартными для автомобильных систем охлаждения! По отрывочным сведениям о других подобных конструкциях, в том числе работающих на воде, там также необходим сначала этап разгона и прогрева до рабочей температуры, и только после этого система выходит на автономный режим работы.
Говоря о центробежных двигателях, мы пришли к выводу о том, что без изменения фазового состояния рабочего тела ничего не получится. В свете этого становится ясно, что достижение определённой температуры, скорее всего, обусловлено именно этим.
Фазы рабочего цикла двигателя Клема
Давайте внимательно рассмотрим цикл рабочего тела в нашей системе и посмотрим, где могут быть происходить изменения фазового состояния рабочего тела, а также отбор энергии, которая может быть преобразована в автономное вращение ротора (и полезной нагрузки)? Говоря об изменении фазового состояния, естественно, имеется в виду переход между жидкостью и газом (паром) и обратно — испарение (кипение) и конденсация. Переход рабочего тела в твёрдое состояние нашей системе в общем случае противопоказан, поэтому возгонка и плавление нас не интересуют, а сублимацию и отвердевание (замерзание) можно рассматривать как ограничивающий фактор.
Пройдём рабочий цикл двигателя Клема, начиная с резервуара с жидкостью, по его «классическому» изображению, попутно обращая внимание на некоторые особенности конструкции. Следует заметить, что в отличие от обычных двигателей с возвратно-поступательным движением поршня, где рабочее тело находится в одном месте (в цилиндре), а фазы определяются положением деталей конструкции, в двигателе Клема рабочее тело двигается непрерывно в одном направлении, и разные фазы рабочего цикла соответствуют прохождению им различных элементов устройства. По аналогии с автомобильными двигателями пространство вокруг конуса, включая резервуар с маслом, для краткости будем называть картером, поскольку функции его те же самые — собирать отработавшее разбрызганное масло и его пары для дальнейшего использования.
Таблица 1.1. Этапы рабочего цикла двигателя Клема
| № |
Фаза |
Агрегатное состояние |
Описание |
| 1 |
Резервуар (картер) |
Жидкость |
Здесь рабочее тело находится в виде жидкости, которая собирается после использования и направляется в теплообменник. |
| 2 |
Теплообменник |
Жидкость |
Температура жидкости выравнивается с температурой окружающей среды. Обычно считается, что в теплообменнике она охлаждается, однако хочу обратить внимание, что этот элемент везде осторожно обозначается именно как «теплообменник», и нигде как «радиатор», «охладитель» и т.п. |
| 3 |
Насос |
Жидкость |
Насос создаёт необходимое давление на входе спирали. При сжатии температура реальной жидкости неизбежно несколько повысится, хотя и отнюдь не так сильно, как это было бы при сжатии газа. Особо заметим, что поскольку теплообменник стоит до насоса, на вход спирали попадает немного «подогретая» сжатием жидкость. |
| 4 |
Спираль на конусе |
Жидкость |
Рабочее тело перемещается к форсункам, при этом под действием центробежных сил давление возрастает. При росте давления температура рабочего тела снова несколько повышается, кроме того, потери энергии на гидродинамическое сопротивление также переходят в тепло. |
| 5 |
Форсунки (сопла) |
Испарение |
Подогретое, а возможно, и перегретое, рабочее тело выпрыскивается через форсунки в свободное пространство над резервуаром. Происходит резкое падение его давления, в результате чего оно расширяется и теряет свою температуру, при этом, как минимум, часть его переходит в пар. Здесь важны параметры как форсунки, так и сопла, позволяющие оптимально использовать кинетическую энергию молекул пара во время его расширения. |
| 6 |
Картер (пространство над резервуаром и стенки корпуса) |
Конденсация |
Расширившийся и потерявший свою температуру пар конденсируется частично в объёме, частично на внутренних стенках корпуса и стекает вниз, чтобы попасть в теплообменник. Неиспарившаяся часть рабочей жидкости также собирается в резервуаре. |
Очевидно, ключевым моментом в рабочем цикле является выпрыскивание рабочего тела из форсунки и истечение его из сопла, которое, собственно, и придаёт вращение конструкции и при котором, по всей видимости, по крайней мере часть рабочей жидкости испытывает фазовый переход, превращаясь в пар и повышая эффективность реактивной тяги форсунок (очевидно, для более эффективного испарения и нужна-то высокая температура, необходимость предварительного разгона и прогрева также косвенно указывает на это). Насколько же при выпрыскивании может измениться температура рабочего тела и какую работу оно может совершить?
Форсунки и сопла
Посмотрим, каким может быть изменение температуры рабочего тела при прохождении им сопла на внешнем конце спирали. Будем считать, что скорость сжатой жидкости на входе сопла достаточно мала, а вот её температура — велика и превышает температуру кипения при атмосферном давлении, которое поддерживается вокруг конуса. В качестве рабочего тела возьмём воду. Выберем внутреннее сечение канала (трубки) равным Sз = 2 см2 («водопроводный» стандарт 1/2"), а сечение сопла Sс = 0.1 см2 (диаметр 3.6 мм). Внутренний диаметр полого вала примем равным 2 см (радиус вращения заборного отверстия спирали будет равен 1 см). Теперь на основе формулы, полученной при анализе центробежных двигателей, сделаем расчёт скорости рабочего тела в спирали и давления возле сопла для нескольких скоростей вращения при давлении на входе спирали 2·106 Па (~20 атм) и внешнем радиусе конуса 15 см.
Таблица 1.2. Расчёт параметров потока в спирали для различных скоростей вращения
Скорость вращения спирали
f |
Расчётное давление возле сопла
PС |
Расчётный расход рабочего тела |
Расчётная скорость потока в канале
vТ |
Расчётная скорость в сопле
vС |
Линейная скорость сопла
v |
| 30 об/сек = 1800 об/мин |
2.35·106 Па ~ 23.5 атм |
0.686 кг/с |
3.43 м/с |
68.6 м/с |
28.3 м/с |
| 35 об/сек = 2100 об/мин |
2.47·106 Па ~ 24.7 атм |
0.704 кг/с |
3.52 м/с |
70.4 м/с |
33.0 м/с |
| 40 об/сек = 2400 об/мин |
2.62·106 Па ~ 26.2 атм |
0.725 кг/с |
3.62 м/с |
72.5 м/с |
37.7 м/с |
Итак, при росте числа оборотов скорости жидкости в трубке и в сопле возрастают не очень сильно, зато центробежная прибавка давления растёт как квадрат скорости вращения — от ~3.5 атм при 1800 об/мин до ~6.2 атм при 2400 об/мин и, в общем, получается немалой — в среднем где-то четверть от создаваемого насосом давления.
Рассмотрим процесс истекания жидкости из сопла. Предположим, что сопло после форсунки (наиболее узкой части канала прохождения жидкости) имеет коническую форму, т.е. сечение канала постепенно увеличивается (для прямого конуса — пропорционально квадрату расстояния от вершины конуса). При этом давление, максимальное при прохождении форсунки, начинает уменьшаться пропорционально текущей площади сечения конуса, высокая скорость же, полученная жидкостью в момент прохождения форсунки, уменьшается незначительно из-за отсутствия существенного сопротивления внешней среды, сравнимого с давлением внутри форсунки.
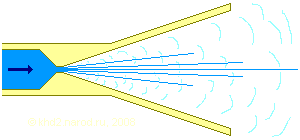 Схема истечения жидкости через форсунку с её частичным испарением в сопле.
Изначально рабочее тело продолжает находиться в жидком состоянии, однако после того, как давление становится меньше критической величины, зависящей от температуры жидкости в форсунке, она оказывается перегретой и часть её превращается в пар. Впрочем, на самом деле это происходит практически сразу, т.к. стоит чуть увеличиться сечению канала, как давление падает очень значительно — ведь при изменении давления объём жидкости практически не меняется (в закрытой трубе поток жидкости после форсунки просто замедлился бы в соответствии с уравнением Бернулли, но у нас сопло открыто и свободному выходу жидкости препятствует лишь атмосферное давление, которое во много раз меньше давления в форсунке). Как только часть жидкости превратилась в пар, он заполняет весь дополнительный объём (ведь скорость его молекул — ~500 м/с — в несколько раз превышает вычисленную нами в таблице 1.2 скорость потока в форсунке — ~70 м/с). При этом он создаёт заметное давление, препятствующее полному испарению оставшегося объёма жидкости, и частично снижает её температуру за счёт теплоты испарения. Впрочем, в силу высокой скорости процесса (всё прохождение сопла занимет доли миллисекунды) не происходит такого существенного охлаждения рабочего тела, оставшегося в жидкой фазе, как это имело бы место в случае более медленного протекания процесса, а расширение образовавшегося пара вообще можно считать адиабатическим. По мере продвижения к срезу сопла его диаметр нарастает, и давление в паро-жидкостной смеси падает, заставляя испаряться всё большее количество жидкости, а температура пара в ходе адиабатического расширения падает. Следует добавить, что стремительно расширяющийся пар способствует разрушению струи, вылетевшей из форсунки, тем самым облегчая испарение оставшейся жидкости.
Рассчитаем количество испарившейся жидкости при различных температурах, считая что парообразование полностью отбирает необходимую теплоту у всей массы жидкости, на примере воды, удельная теплоёмкость которой равна 4.19·103 Дж / (кг · К), а соотношение изобарической и изохорической теплоёмкостей для водяного пара γ = 1.28. Предположим также, что процесс расширения образовавшегося при соответствующем давлении пара является адиабатическим и на основе уравнения адиабаты определим понижение его температуры при падении давления до атмосферного. Результаты занесём в таблицу (в уравнении адиабаты, естественно, учитывается абсолютная температура, но в таблице она для удобства восприятия переведена в градусы Цельсия).
Таблица 1.3. Испарение и расширение пара в сопле
| Давление при закипании (на нижней температурной границе диапазона) |
Диапазон изменения температуры жидкости |
Теплота парообразования |
Доля вскипевшей жидкости при понижении температуры на 10° |
Температура пара после адиабатического расширения до атмосферного давления |
| 5.9·105 Па (~5.8 атм) |
170°С → 160°C |
2.08·106 Дж / кг |
2.01% |
–9°C |
| 4.85·105 Па (~4.8 атм) |
160°С → 150°C |
2.11·106 Дж / кг |
1.99% |
0°C |
| 3.8·105 Па (~3.8 атм) |
150°С → 140°C |
2.14·106 Дж / кг |
1.96% |
12°C |
| 2.8·105 Па (~2.8 атм) |
140°С → 130°C |
2.17·106 Дж / кг |
1.93% |
30°C |
| 1.95·105 Па (~1.9 атм) |
130°С → 120°C |
2.20·106 Дж / кг |
1.90% |
79°C |
| 1.5·105 Па (~1.5 атм) |
120°С → 110°C |
2.23·106 Дж / кг |
1.88% |
54°C |
| 1.01·105 Па (1.0 атм) |
110°С → 100°C |
2.26·106 Дж / кг |
1.85% |
100°C |
Следует подчеркнуть интересный эффект — чем выше температура перегретой жидкости, и, следовательно, давление, при котором она вскипает после выхода из форсунки, тем ниже температура пара после его адиабатического расширения, которая вполне может достигнуть точки замерзания рабочего тела, а при ещё большем перегреве жидкости перед форсункой — вот парадокс — даже оказаться ниже точки замерзания! Куда же девается теплота, потерянная расширяющимся паром? Термодинамика даёт только один ответ — она должна превратится в механическую работу, выбрасывающую пар из сопла и добавляющая реактивную тягу к той, что обусловлена немалой кинетической энергией струи в форсунке, но недостаточна для саморазгона ротора.
Обеспечить жидкое состояние перегретого рабочего тела не представляет проблемы — создаваемого насосом и центробежными силами давления, как мы выяснили, более чем достаточно, чтобы удерживать перегретую воду в жидком состоянии не только при 150..170°С, но и при гораздо более высоких температурах.
К доле же испаряющейся жидкости в данном случае следует относится как к справочной информации — как уже отмечалось выше, в процессе испарения в сопле перейти в пар должен практически весь объём жидкости, поскольку из-за высокой скорости теплообмен между оставшейся жидкостью и образующимся паром будет весьма незначительным, и температура ещё неиспарившейся перегретой жидкости понизится несущественно.
Заметим, что при этом условие скорости истечения жидкости из сопла, превышающей линейную скорость вращения сопла, уже не является принципиально важным для создания реактивной тяги. Здесь тяга уже обусловлена количеством образовавшегося пара и скоростью движения его молекул, которая на дозвуковых скоростях движения сопла заведомо превышает линейную скорость сопла.
Необходимое дополнение. Всё вышесказанное верно при условии, если нет конденсации пара при более высоких температурах. В обычных условиях при достижении температурой «точки росы» начинается его конденсация с выделением существенного количества тепла (достаточного для нагрева того же количества воды в жидкой фазе примерно на 80°, а в виде пара — примерно на 150°). Температура «точки росы» зависит от абсолютной концентрации пара и может быть весьма высокой — как только относительная влажность достигает 100%, начинается конденсация. Таким образом, для полного адиабатического охлаждения необходимо поддерживать крайне низкую концентрацию пара, что в замкнутом пространстве очень сложно и возможно лишь при условии интенсивного удаления пара из области испарения. Эти жёсткие ограничения делают охлаждение расширяющегося пара до температуры ниже окружающей среды крайне затруднительным — ещё один аргумент против термодинамической причины работы двигателя Клема.
Но всё же допустим, что мы нашли предположительный источник работы двигателя Клема (если рассматривать его как тепловую машину) — это энергия, высвобождающаяся при испарении (хотя бы частичном) рабочей жидкости на выходе из форсунки и дающая добавочную реактивную тягу, позволяющую раскручивать ротор. Однако перед форсункой жидкость должна быть перегрета, и чем больше — тем лучше. Но откуда берётся тепло, необходимое для её разогрева, ведь никакого топлива нет?!
Конус — главная деталь
Конус со спиральными каналами, очевидно, изготовлен из металла (вряд ли в 1970-х годах Клем выбрал бы пластик — в те времена в широком доступе не было подобных материалов, способных неизменно сохранять свою форму и высокие физические свойства при длительной работе в условиях высоких нагрузок и температур; камень и дерево также вряд ли заинтересовали бы его по очевидным причинам). Но ведь одно из характерных свойств металлов, помимо прочности и стойкости к нагреву — это высокая теплопроводность! Не используется ли каким-нибудь образом это свойство в работе двигателя, и вообще, высокая теплопроводность и хороший теплообмен в конусе — это благо или зло для данной конструкции?
Общая схема переноса тепла в конусе
Итак, предположим, что двигатель находится в рабочем состоянии — к форсункам подаётся перегретая жидкость, которая затем выпрыскивается, охлаждается при расширении, собирается в поддоне-картере, проходит через теплообменник, приобретая температуру окружающей среды и после насоса подаётся на начало спирального канала в конусе. Что же происходит в самом конусе?
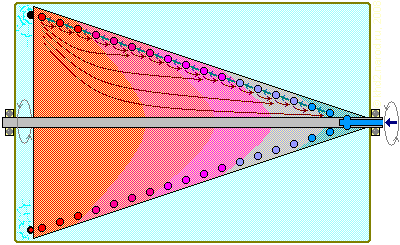 Предположительная схема теплообмена в массивном роторе двигателя Клема. Тёмно-красные стрелки — перенос тепла в теле конуса за счёт теплопроводности, тёмно-голубые — перенос тепла рабочим телом за счёт его теплоёмкости.
Допустим, что конус представляет собой массивную металлическую болванку, в теле которой сделаны спиральные каналы. Будем считать, что после теплообменника на входе в насос рабочая жидкость имеет температуру, близкую к температуре окружающей среды. Насос нагнетает её в конус, повышая давление и несколько повышая температуру. Далее жидкость начинает двигаться по спиральному каналу внутри конуса от его относительно холодной вершины (температура равна температуре на выходе насоса) к горячему основанию (температура равна температуре перегретой жидкости в форсунках). Двигаясь по спиральному каналу, рабочая жидкость за счёт теплопроводности материала конуса получает тепло от более горячих частей конуса, расположенных ближе к его основанию. Однако это тепло не теряется — ведь рабочая жидкость по мере своего движения благодаря своей теплоёмкости возвращает это тепло туда, откуда она его получила благодаря теплопроводности — к основанию конуса! Таким образом, при должном балансе скорости жидкости и сечения канала (точнее, площади его стенок), определяющих теплообмен между конусом и жидкостью на единицу длины канала и скорость возврата тепла к основанию конуса, и сечения самого конуса и плотности размещения витков спирали, определяющих подвод тепла к стенкам канала от горячего основания конуса, ротор двигателя Клема представляет собой почти замкнутую тепловую систему, в которой тепло перемещается от горячего основания конуса к его более холодной вершине за счёт теплопроводности материала конуса и возвращается обратно потоком рабочей жидкости благодаря её теплоёмкости. Однако это система замкнута не полностью, а почти, потому что часть тепла уносит выпрыскиваемая через форсунки рабочая жидкость, расходуя его на механическую работу по раскручиванию конуса. В то же время, перемещаясь по спирали, рабочая жидкость испытывает дополнительное сжатие за счёт центробежных сил и трение о стенки канала. Оба эти процесса преобразуют механическую энергию вращения ротора и потока жидкости в тепло, которое и должно компенсировать потери тепла, выносимого жидкостью через форсунки. При этом основную роль, по всей видимости, играет именно жидкостное трение, тепловой потенциал которого нельзя недооценивать — вспомним автомобильные коробки передач, в первую очередь автоматические, которые во время работы разогреваются очень существенно, а ведь главная причина этого общеизвестна — это жидкостное трение заполняющего их масла.
Таким образом, массивный конус выступает в роли как нагревателя, так и накопителя тепла, необходимого для перегрева рабочей жидкости. При этом накопление энергии выполняется в режиме резонанса, что крайне необычно для тепловой техники. Очевидно, что длительный разбаланс между переносом тепла потоком жидкости и обратной передачей тепла через материал конуса выведет двигатель из рабочего режима. Впрочем, экстремальные режимы работы мы рассмотрим чуть позже. Пока же можно сказать лишь, что в рамках этой гипотезы конус должен быть по возможности теплоизолирован от окружающей среды с целью сокращения непроизводительных потерь тепла.
Кажется, что основная функция конуса — именно накопление тепла. Но присмотримся внимательнее, так ли это? Да и вообще, есть ли польза от описанного выше механизма в нашем случае?
Уточнённая схема теплообмена в конусе
Мы предположили, что поступающая в конус жидкость нагревается за счёт встречного переноса тепла от более горячих частей конуса, расположенных ближе к форсункам. Однако, в конце концов, что-то же должно нагревать эту самую часть конуса возле форсунок! И другого источника, кроме как нагрев от трения рабочей жидкости в спиральном канале у нас нет (увеличение давления, конечно, тоже может вносить свою лепту, но, поскольку жидкости являются практически несжимаемыми субстанциями, тепловой вклад от сжатия я оцениваю как очень незначительный). Таким образом, взаимное распределение температур конуса и жидкости на различных участках спирали представляет собой более сложную картину, чем простая передача тепла от конуса к жидкости или обратно.
 Соотношение температур конуса и рабочей жидкости в роторе двигателя Клема. Красная линия — температура конуса, синяя линяя — температура рабочей жидкости. Участок a — нагрев жидкости конусом за счёт теплопроводности; участок б — нагрев конуса рабочей жидкостью за счёт жидкостного трения.
Итак, сначала жидкость, поступившая в конус, нагревается в основном за счёт теплообмена с более горячим материалом конуса (участок а). Затем температура жидкости достигает температуры конуса у стенок спирали и дальнейшей нагрев жидкости уже происходит целиком за счёт её трения и дополнительного сжатия центробежными силами (участок б). При этом температура жидкости становится выше температуры конуса, и часть своего тепла жидкость отдаёт конусу, а оно, в свою очередь, идёт на нагрев вновь поступивших порций рабочей жидкости у вершины конуса.
Граница между этими участками весьма условна и смещается по конусу взад или вперёд в зависимости от режима работы. Например, при раскрутке в начале работы конус холодный, и вся спираль работает в режиме б. С другой стороны, при замедлении вращения конуса длина участка а увеличивается, и при полной его остановке почти вся спираль начинает работать именно в этом режиме, отдавая тепло конуса рабочей жидкости. Но, конечно, наиболее интересен установившийся режим работы. Здесь можно предположить следующее. Поскольку обычно нагрев за счёт теплообмена происходит значительно быстрее, чем нагрев за счёт жидкостного трения, большая часть спирали работает в режиме б, а меньшая — в режиме а, при этом чем меньше вязкость рабочей жидкости, тем больше соотношение б / а.
И последнее, но самое главное замечание насчёт теплового баланса в конусе. Тепло, полученное за счёт трения рабочей жидкости при прохождении по спирали и при дополнительном сжатии жидкости центробежными силами должно быть равно теплу, запасённому ею при нагреве от температуры на входе в спираль до температуры на выходе из спирали возле форсунок. Однако это требование справедливо только для длительного режима работы. Небольшие отклонения как в ту, так и в другую сторону, вызванные изменениями режима работы, вполне допустимы, однако они должны быть быстро скомпенсированы, иначе двигатель выйдет из рабочего режима. Следовательно, главный критерий минимальной длины спирали — необходимость получения достаточного количества тепла прежде всего за счёт трения при прохождении по конусу. Отсюда следует вывод — конус совсем необязательно должен быть массивным и совсем необязательно должен накапливать большое количество тепла, хотя это и может быть желательно для обеспечения стабильности работы. Однако спираль обязательно должна быть достаточно длинной, а трение жидкости в ней следует увеличивать всеми возможными методами, либо попытаться применить другие способы преобразования кинетической энергии потока жидкости в тепло!
Замыкая круг
Теперь мы можем описать полный рабочий цикл двигателя Клема как тепловой машины, указав, откуда энергия берётся и куда она девается. Итак, в рабочем режиме жидкость нагревается при нагнетании её насосом (за счёт механической энергии ротора, приводящего насос в движение), и далее нагревается в спирали за счёт дополнительного сжатия центробежными силами и при трении о стенки спирали (в конце концов, снова за счёт механической энергии ротора), но главным образом за счёт теплообмена с разогретым конусом. Далее перегретая жидкость выпрыскивается через форсунки, превращаясь, по крайней мере частично, в пар, и разгоняя ротор с помощью реактивной тяги, значительную часть которой даёт тепловая энергия полученного пара. При расширении в сопле пар теряет температуру и охлаждается ниже температуры окружающей среды, затем конденсируется в объёме и на стенках корпуса, в котором находится ротор, после чего холодная жидкость попадает в теплообменник, где нагревается до температуры окружающей среды и вновь подаётся на вход насоса.
Вот эта-то отобранная у внешней среды тепловая энергия и превращается в полезную механическую работу, так что в рабочем состоянии теплообменник и объём вокруг конуса внутри корпуса двигателя должны быть холодными, а горячим является конус, причём у вершины — лишь слегка тёплым, а у основания — перегретым относительно точки кипения рабочей жидкости. Следует заметить, что размеры теплообменника не должны быть слишком большими. Глядя на те же автомобили, можно заметить, что радиатора размером 40x50 см с вентилятором обычно вполне достаточно для охлаждения двигателей мощностью 150 л.с. (~100 кВт) и даже больше, т.е. для отведения этой мощности в окружающую среду. При этом перепад температур между температурой мотора (+90°С) и окружающей среды (+40°С и выше в жару на солнцепёке) может составлять менее 50°. В случае двигателя Клема на воде расчётный перепад может составить 10..15°С (+20°C в комнате и +5..+10°С сконденсировавшейся жидкости в картере, чтобы избежать обледенения), — для передачи той же мощности это потребует несколько больших размеров теплообменника, но не намного. Кроме того, можно выбрать и другие рабочие жидкости с более низкой температурой замерзания, обеспечив возможность работы двигателя не только летом или в комнате, но и зимой на улице, и использовать более низкую температуру конденсата.
Итак в общих чертах картина прояснилась. Однако пока мы рассуждали, оперируя лишь качественными категориями. Но прежде, чем строить наш воздушный замок дальше, было бы неплохо проверить «гармонию алгеброй» и посчитать всё на конкретных цифрах, чтобы потом «вдруг» не выяснилось, что мы долго и с энтузиазмом надували заведомый мыльный пузырь...
Оценка энергетического баланса
Попробуем оценить энергетический баланс двигателя Клема. Расчёт выполним, используя в качестве рабочего тела воду (дистиллированную, чтобы не было накипи), поскольку для неё достаточно полные необходимые данные найти проще всего — прежде всего, это удельная плотность и удельная теплоёмкость в жидком состоянии при различных температурах, а также зависимости от давления температуры, удельной теплоты парообразования и удельной теплоёмкости пара и соотношение изобарической и изохорической теплоёмкостей для оценки падения температуры при адиабатическом расширении. Этот же расчёт является примером выбора некоторых базовых параметров конструкции. Итак, базовые параметры для расчёта: рабочее тело — вода, температура окружающей среды — +25°С, номинальная скорость вращения — 1800 об/мин (30 об/сек), радиус вращения форсунок — 15 см.
Первым делом необходимо выбрать температуру перегретой жидкости у форсунок. Не будем связываться с замерзанием рабочей жидкости и возможными при этом проблемами обледенения, поэтому выбираем температуру пара в конце адиабатического расширения не ниже 0°С. По ранее проведённым расчётам, этому соответствует температура перегретой жидкости 150°С и давление на входе сопла чуть менее 500 кПа (5 атм). Поскольку мы уже выяснили, что при заданной скорости вращения прибавка давления за счет центробежных сил составляет порядка 350 кПа (3.5 атм), насос на входе ротора должен создавать давление не менее 1.5 атм (150 кПа) — значение весьма невысокое, соответствующее примерно 15-метровой высоте водяного столба. Сделав небольшой запас на непредвиденные обстоятельства, примем создаваемое насосом давление равным 2 атм. С целью обеспечения не слишком высокой скорости движения жидкости в конусе выберем соотношение площади отверстия форсунки к сечению спирального канала равным 1:20.
Теперь посчитаем изменение тепловой энергии с учётом фаз рабочего цикла. С плюсом запишем этапы, увеличивающие внутреннюю энергию рабочего тела (нагрев), а с минусом — уменьшающие её (охлаждение). Поскольку испарение перегретой жидкости предполагается за счёт её накопленной внутренней энергии, теплоту испарения считаем отрицательной, а вот при конденсации выделяющееся тепло должно остаться в замкнутом объёме двигателя и, в конечном счёте, нагреть жидкость, поэтому теплоту конденсации считаем положительной.
Таблица 1.4. Тепловой баланс рабочего цикла
| Фаза рабочего цикла (в соответствии с таблицей 1.1 |
Температура по окончании фазы |
Изменение энергии 1 кг воды, Дж |
Баланс энергии 1 кг воды, Дж |
| На выходе теплообменника (после фаз 1 и 2) |
25°С |
+104 750 (нагрев в теплообменнике с 0°С) |
104 750 |
| После насоса под давлением 2 атм (фаза 3, объём уменьшился на 0.01%) |
25°С |
0 |
104 750 |
| Перед форсункой (фаза 4, при нагреве объём увеличился на 9%) |
150°С |
+523 750 (нагрев в конусе с 25°С) |
628 500 |
| После испарения перед расширением (начало фазы 5) |
150°С |
-2 120 000 (теплота парообразования) |
-1 491 500 |
| После адиабатического расширения пара (конец фазы 5) |
0°С |
-285 000 (охлаждение пара со 150°С), |
-1 776 500 |
| После конденсации (фаза 6) |
0°С |
+2 500 000 (теплота парообразования / конденсации) |
723 500 |
Итак, имеет место огромная прибавка энергии — более 700 кДж на 1 кг воды. Теоретически, эта теплота может быть полностью преобразована в механическую работу, однако в реальности часть этой полезной работы используется для приведения в движение механических элементов установки, включая компенсацию потерь на трение, а часть — просто недополучена вследствие неполного испарения и других неизбежных отклонений от идеального цикла. Прежде всего, отсюда следует вычесть затраты энергии на нагрев воды с 25°С до 150°С в фазе 4, который должен осуществляться за счёт полученной механической энергии, в результате чего у нас остаётся «чистых» 200 кДж. Однако и это, мягко говоря, очень немало, и, кстати, почти вдвое превышает энергию, которую мы предполагаем отобрать у внешней среды в теплообменнике для нагрева жидкости от 0°С до 25°С.
Этот остаток, которого вполне хватит на ощутимый полезный выход, никак нельзя списать на кинетическую составляющую (при давлении на входе конуса около 2 атм в момент выхода из форсунки с расчётной скоростью 33 м/с 1 кг воды имеет лишь 0.54 кДж кинетической энергии, что ничтожно мало). Она образуется за счёт различных удельных теплоёмкостей жидкой и парообразной фаз, а также существенно разных значений теплоты парообразования и конденсации воды при различных температурах.
Кстати, подобная разность теплоты парообразования при высокой и низкой температуре характерна практически для всех жидкостей, да и теплоёмкость паров обычно меньше, чем у жидкой фазы, — интересно, будет ли работать двигатель, если в течение рабочего цикла температура рабочего тела не будет опускаться ниже температуры окружающей среды? Правда, это окажется вопиющим нарушением законов классической термодинамики, но зато будет соответствовать описанию работы двигателя Клема, если считать теплообменник охладителем...
А как же с балансом энергии? И здесь всё нормально: полезная работа в конце концов во внешней среде превращается в тепло, которое через теплообменник возвращается в систему «двигатель — полезная нагрузка — внешняя среда — двигатель». Впрочем, взглянув на это с точки зрения классической термодинамики, мы должны будем сказать, что полученный в результате подведения баланса выход энергии в 200 кДж с каждого килограмма воды — пиковый. В длительном режиме он не может превышать энергию, получаемую через теплообменник — около 100 кДж, иначе рабочее тело заберёт слишком много тепла, система остынет и может выйти из рабочего режима, а всё «лишнее» тепло на самом деле не лишнее и через механическую работу идёт на разогрев очередных порций жидкости. Но ведь в расчёте баланса мы уже учли затраты на нагрев жидкости, и получается что почти 100 кДж / кг — это «чистый» выигрыш! М-да, либо где-то вкралась ошибка, либо...
Несколько больших «НО»...
Этот пункт я вставил примерно через полгода после написания основного текста этой страницы, придя к твёрдому убеждению, что отбор тепла из внешней среды не является причиной работы двигателя Клема, и его теплообменник не может быть холодным. Прежде всего, это тот факт, что в предполагаемом прототипе конус и его форсунки выходят не в газовую среду, а в заполненную жидким рабочим телом (маслом) выходную камеру. Даже если бы они выходили в газовую среду, сильному охлажденнию пара мешала бы конденсация в «точке росы», температуру которой снизить очень непросто. Но и при решении этой проблемы успех отнюдь не гарантирован. Какие факты не были учтены при анализе баланса?
Во-первых, чтобы получить из потенциальных тепловых 723 кДж реальные механические 524 кДж (а это минимум, который по вышеприведённому расчёту необходим для механического разогрева воды), необходимо иметь КПД этого преобразования выше 72%. Для современных тепловых машин это очень неплохой показатель, вряд ли достижимый для столь примитивной турбины, которая подразумевается в конструкции нашего конуса и уж тем более в насосе-прототипе, где вообще отсутствовали какие-либо специальные сопла. Кроме того, предполагаемый при составлении баланса режим работы требует практически мгновенного удаления расширившегося пара из области, куда он выпрыскивается из сопел, т.е. высокоэффективную конденсацию и откачку. Реализация этого условия естественным путём не представляется реальной (разве что эта область будет размером с ангар, по стенкам которого и будет стекать конденсат — но там возникают другие проблемы). Всё остальное требует принудительного охлаждения, а стало быть, и затрат энергии. Иначе давление в приёмной камере будет расти и параметры образования пара отклонятся от расчётных — в худшую для нас сторону.
Во-вторых, всё же подавляющее количество пара будет образовываться при температуре, близкой к 100°С, — иначе вылетающие из форсунки перегретые капельки должны состоять буквально из нескольких молекул воды, а размеры их не превышать нанометра. В силу многих причин это представляется технически нереальным. Для более крупных капелек (даже диаметром в микрометр) их внутренняя часть будет охлаждаться до температуры кипения вне сопла (т.е. при атмосферном давлении — до 100°С) за счёт испарения внешних слоёв, и теплота парообразования сушественно возрастёт по сравнению с перегретой до 150°С водой (с 2120 до 2260 кДж/кг). В результате «лишняя» энергия сократится с 200 кДж менее чем до сотни. Добавьте изложенное в предыдущем абзаце, и картина станет совсем не оптимистичной, а необходимый КПД преобразования «тепло — механическая работа» будет приближаться к 100%.
Что говорит закон сохранения энергии?
Закон сохранения энергии утверждает, что для того, чтобы получить и затем потратить какое-либо количество энергии, сначала нужно его откуда-то взять. Получить энергию можно, например, «перекачав» её из внешней среды, как это делают тепловые насосы, в частности некоторые модели кондиционеров, либо преобразовать её из другой формы — механической (совершение работы и нагрев при торможении), электрической (скажем, с помощью нагревательных элементов), химической (сжечь топливо) и т.д. В любом случае, если где-то чего-то прибывает (тепла, совершённой механической работы и т.д.), то где-то чего-то и убывает (топлива, скорости и т.п.).
Однако в рассчитанном балансе мы видим прибыль тепловой энергии, видим совершённую механическую работу и не видим, что же должно убывать — в соответствии с описанием работы двигателя Клема и в противоречии с законом сохранения энергии. Тем не менее, я считаю, что и в этом случае энергия не возникает сама по себе, а перетекает из каких-то других форм. Откуда именно — пока не ясно, гипотезы на этот счёт могут быть какие угодно, — от «мирового эфира» до «фазовых переходов высшего рода». Впрочем, решением этого вопроса можно будет заняться, когда (и если!) заработает опытный образец — на его примере...
Что говорит эксперимент?
Экспериментальные данные о теплоте испарения или конденсации насыщенного водяного пара и его теплоёмкости при различных температурах и давлениях можно найти практически в любом справочнике по физике. Поскольку теплоёмкость жидкой воды зависит от температуры очень слабо (при изменении температуры на 10° её теплоёмкость меняется на сотые доли процента), эту зависимость найти труднее — обычно приводится обобщённое значение в диапазоне 4118..4120 Дж / (кг · К), но этого, как правило, вполне достаточно для инженерных расчётов.
Кроме того, экспериментально установлено, что для одного и того же вещества при одних и тех же значениях температуры, давления и степени насыщенния парами теплота, поглощаемая при испарении, равна теплоте, выделяющейся при конденсации, а теплоёмкость при нагревании равна теплоёмкости при охлаждении. Посмотрим, каковы эти данные для воды при температуре испарения при нормальном давлении и при перегреве, скажем, до 150°С (под давлением около 5 атм). При повышении температуры теплоёмкость парообразования снижается (в нашем случае — почти на 7%), а теплоёмкость пара повышается приблизительно на 60..70% — с 26% до примерно 40%..45% от теплоёмкости жидкой фазы (к сожалению, точных данных о теплоёмкости пара для 150°С у меня нет, поэтому оценка приблизительна; для 200°С теплоёмкость пара составит 48% теплоёмкости жидкой фазы).
Что следует из экспериментальных данных?
Таким образом, если перегреть жидкую фазу, затем при температуре перегрева эту жидкость испарить, переведя в парообразное агрегатное состояние, далее провести адиабатическое расширение до нормального давления, по окончании которого сконденсировать его, то в результате такого цикла мы можем получить избыток тепловой энергии, для которой я не вижу никакого выхода, кроме как совершения механической работы при расширении пара. При этом излишки теплоты образуются за счёт разницы теплоты испарения перегретой жидкости и теплоты конденсации переохлаждённого пара, а условием получения такого избытка является превышение этой разницей разности энергий нагревания и охлаждения рабочего тела из-за различия его теплоёмкостей в разных агрегатных состояниях. В расчёте будем использовать справочные данные, которые, как известно, обычно получают экспериментальным путём.
Составим таблицу для различных величин перегрева воды в диапазоне от 100° до 200°С. Теплоёмкость жидкой воды везде принята равной 4.12 кДж / (кг · К), базовая температура 100°С (перед нагревом), давление при конденсации 1 атм (1.013·105 Па), соотношение изобарической и изохорической теплоёмкостей 1.29. С плюсом указана энергия (теплота), отдаваемая рабочим телом вовне, а с минусом — получаемая им оттуда. Теплоёмкость пара принята равной 1800 Дж / кг, что является приблизительной величиной, но более точных данных у меня, к сожалению, пока нет.
Таблица 1.5. Тепловой баланс полного рабочего цикла с адиабатическим расширением для 1 кг воды.
| Перегрев |
Давление перегрева, Па (атм) |
Температура после расширения |
Средняя теплоёмкость пара для нулевого баланса, кДж / кг |
Теплота нагрева, кДж |
Теплота испарения, кДж |
Теплота расширения пара, кДж |
Теплота конденсации, кДж |
Теплота нормализации температуры до 100°С, кДж |
Баланс энергии, кДж |
| 100°С |
1.013·105 (1.0) |
100°C |
любая
(реально — 1103) |
0 |
-2260 |
0 |
2260 |
0 |
0 |
| 110°С |
1.5·105 (1.5) |
+69°C |
1693 |
-41 |
-2230 |
74 |
2330 |
-129 |
4 |
| 120°С |
1.96·105 (1.94) |
+52°C |
1798 |
-82 |
-2206 |
123 |
2365 |
-199 |
0 |
| 130°С |
2.90·105 (2.86) |
+24°C |
1855 |
-123 |
-2170 |
191 |
2410 |
-313 |
-6 |
| 140°С |
3.8·105 (3.77) |
+8°C |
1687 |
-164 |
-2140 |
237 |
2460 |
-377 |
15 |
| 150°С |
4.87·105 (4.80) |
-3°C |
1581 |
-206 |
-2110 |
284 |
2500 |
-427 |
34 |
Следует заметить, что если в качестве теплоты конденсации использовать значение для 100°С (2260 Дж / кг), баланс энергии во всех случаях будет сильно отрицательным. Таким образом, обязательным условием положительного энергетического баланса является конденсация переохлаждённого пара при температуре, если и не равной, то очень близкой к температуре в конце его адиабатического расширения. Именно наиболее полное проведение адиабатического расширения с получением переолаждённого пара является непременным условием, без соблюдения которого ожидать положительного энергетического баланса вообще не имеет смысла. Практическая реализация этого условия представляется маловероятной.
Также надо отметить, что при относительно небольшом перегреве (ниже 140°С) и, соответственно, не слишком большом давлении испарения в сочетании с довольно высокими температурами переохлаждённого пара, баланс энергии колеблется около нуля (небольшие отклонения могут быть связаны с погрешностями аппроксимации данных), и лишь при перегреве от 140°С и выше получение предполагаемой «лишней» энергии выглядит достаточно устойчивым, но тут нас подстерегает другое ограничение — температура переохлаждённого пара становится ниже температуры замерзания воды.
Наконец, следует оговориться, что расчёт в диапазоне 110°С..140°С я оцениваю как очень приблизительный, поскольку реальная теплоёмкость пара там, скорее всего, существенно меньше расчётной, а это кардинальным образом ухудшает результаты. Однако по мере роста перегрева необходимая минимальная теплоёмкость снижается, в то время как его реальная теплоёмкость растёт, и это позволяет говорить о некоторых возможностях, возникающих в этом диапазоне. Правда, на практике рассуждения эти применить вряд ли удастся — уж слишком жёсткие требования необходимо выполнить для их проявления. К тому же нельзя забывать, что мы имеем дело с экспериментальными данными, которые могут оказаться не слишком точными, — а ведь наш гипотетический выигрыш составляет доли процента от используемых в расчёте величин и вполне может быть меньше погрешностей их определения, связанных как с неизвестной нам точностью измерений, так и с погрешностями, обусловленными самой методикой их проведения, также нам неизвестной.
И всё же...
И всё же, я по-прежнему считаю, что необходимо до конца попробовать пройти «термодинамический путь» — это поможет и при анализе других возможных причин работы. Однако прежде, чем обсуждать детали конструкции двигателя, надо посмотреть (пока без конкретных цифр — лишь в общих чертах), как он мог бы вести себя в различных режимах работы — при старте, на холостом ходу, при резком увеличении нагрузки, при внезапной остановке.
Предполагаемые режимы работы двигателя Клема
Обычный рабочий режим прогретого гипотетического двигателя мы уже описали чуть выше. Теперь рассмотрим экстремальные и переходные режимы работы и управление мощностью.
Начало работы
В начале работы будем считать, что температура всех частей двигателя одинакова и равна температуре окружающей среды. Теперь в соответствии с классической схемой двигателя включаем стартёр. Он начинает раскручивать главный вал с ротором и связанный с ним насос, который подаёт рабочую жидкость в спираль. Постепенно жидкость заполняет спираль и начинает выпрыскиваться через форсунки, своей реактивной тягой облегчая работу стартёра. Однако, как мы выяснили, рассматривая механические центробежные двигатели, этого ещё недостаточно для самостоятельной работы двигателя. Одновременно рабочая жидкость начинает разогревать конус и разогревается сама, причём во всём объеме двигателя — ведь пока ещё нет испарения, нет фазового перехода, нет и адиабатического охлаждения, так что на этом этапе теплообменник можно бы вообще отключить для ускорения выхода двигателя на рабочий режим. Тем не менее, следует заметить, что и здесь конус вблизи основания будет разогреваться быстрее по сравнению со средней температурой рабочей жидкости в двигателе. Источник энергии для всего этого очевиден — это стартовый двигатель.
Чем быстрее вращается конус, тем большее дополнительное давление создают центробежные силы, тем быстрее движется рабочая жидкость в спиральных каналах, тем больше её нагрев от сжатия и трения, разогревающий конус.
Наконец, температура жидкости вблизи форсунок, а стало быть, и температура этой части конуса превышает температуру кипения — жидкость начинает испаряться, возникает дополнительная (по сравнению с просто выпрыскиваемой жидкостью) реактивная тяга, пока ещё слабая. Расширившийся пар тоже пока ещё отнюдь не холодный — ведь температура жидкости в форсунках ещё ненамного превышает температуру кипения (см. таблицу 1.3). Однако и жидкость на входе в насос пока ещё теплее, чем окружающая среда, а это облегчает дальнейшей прогрев конуса. И только когда температура возле форсунок становится настолько большой, чтобы перегретая жидкость вскипала даже при достаточно высоком давлении, адиабатическое расширение от которого понижает температуру пара ниже внешней, теплообменник начинает забирать тепло из окружающей среды и двигатель выходит на автономный режим работы — стартёр можно отключать.
Возможна ситуация, когда стартёр можно отключать и раньше — если тепловой энергии, запасённой в жидкости в картере при первичном разгоне, достаточно для догрева конуса до необходимой температуры. Очевидно, что для этого объём жидкости в картере должен быть достаточно велик, а температура жидкости возле форсунок должна как минимум превышать температуру кипения рабочей жидкости при атмосферном давлении.
Холостой ход
Теперь рассмотрим работу двигателя Клема на холостом ходу, т.е. без нагрузки. Будет ли он раскручиваться бесконечно (в реальности — до разрушения от слишком большой скорости вращения), либо существуют какие-то факторы, способные автоматически ограничить его максимальную скорость вращения?
Итак, предположим, что двигатель запустился, перешёл в автономный режим работы (стартёр выключен) и продолжает увеличивать обороты. Что при этом произойдёт?
Очевидно, что температура основания конуса будет продолжать нарастать и рабочая жидкость начнёт вскипать в сопле при всё более высоком давлении, а температура расширившегося пара — всё более снижаться. В конце концов, она опустится ниже точки замерзания, и пар будет не конденсироваться, а сублимироваться — сразу превращаться в иней, приближая температуру жидкости в картере к точке замерзания. В результате частичного замерзания поток жидкости начнёт уменьшаться, что приведёт к уменьшению реактивной тяги и замедлению вращения ротора.
Возможен и другой вариант развития событий — если давление у форсунок окажется недостаточно велико для того, чтобы удерживать перегретую жидкость в жидком состоянии, она начнёт вскипать перед форсунками, проходя их уже в виде газа. При этом давление в форсунке перестанет расти, поскольку плотность пара при условиях, далёких от критической точки, существенно ниже плотности жидкости и центробежная добавка давления будет меньше. Соответственно, снижается температура и давление пара в форсунке, реактивная тяга уменьшается и ротор несколько замедляется.
Существует и третий вариант ограничения скорости — когда теплообмен между конусом и окружающей его атмосферой внутри корпуса (как известно, его скорость пропорциональная разности температур) не позволит конусу нагреться слишком сильно — из-за большой разности температур между горячим основанием конуса и холодной атмосферой внутри корпуса паразитные потери тепла не дадут основанию конуса перегреться слишком сильно. Этот вариант кажется наиболее «мягким» и потому наиболее предпочтительным.
Если же рассматривать конструкцию вероятного прототипа, то там по мере увеличения скорости, и следовательно, вызванного центробежными силами давления, увеличиваются усилия, стремящиеся расширить зазор между корпусом и конусом и следовательно, увеличить обратный ток рабочей жидкости — получается своего рода предохранительный клапан, обусловленный самой конструкцией этого устройства.
Таким образом, существует несколько факторов, каждый из которых не даст двигателю Клема «пойти в разнос» и автоматически ограничит скорость его вращения. Какой именно из них сработает первым, зависит от особенностей конкретной конструкции. Ну и, конечно, в запасе всегда есть старые добрые специальные средства, такие как предохранительные и перепускные клапаны, открывающиеся при излишне больших давлениях или нагрузках.
Повышение нагрузки
Очень важно, как поведёт себя двигатель при повышении нагрузки. Хороший двигатель при резком повышении нагрузки и снижении оборотов должен стараться автоматически компенсировать это повышением крутящего момента, хотя бы в течение короткого промежутка времени, пока не сработает управление мощностью, учитывающее возросшую нагрузку.
Самый простой метод обеспечить такую реакцию — это запасти механическую энергию в маховике. Для этого в двигателе Клема есть всё необходимое — ведь он имеет ротор, который заодно играет роль маховика. Главное, чтобы при резком возрастании нагрузки тяжелый конус не провернулся на валу!
Помимо механической энергии, запасённой ротором-маховиком, при резком замедлении вращения на короткое время увеличивается и тяга от форсунок — температура конуса, а следовательно и жидкости возле форсунок, меняется относительно медленно, да и давление изменится не сильно — центробежная его составляющая уменьшается, зато увеличивается скоростной напор жидкости, которая пытается сохранить свою прежнюю скорость. А замедление форсунки относительно окружающего воздуха при сохранении прежней скорости струи увеличит её тягу за счёт большего «упора» в воздух. Впрочем, это очень кратковременный эффект, несравнимый с механической энергией, запасённой ротором, поэтому большой тяговитостью двигатель Клема похвастаться вряд ли сможет — при повышении нагрузки необходимо как можно быстрее увеличить и мощность.
Внезапная остановка
Внезапная остановка ротора и механически связанного с ним нагнетателя приводит к падению давления в спиральных каналах. При этом на тех участках канала вблизи форсунок, где жидкость перегрета, она вскипает. Образовавшийся пар продолжает выходить через форсунки, создавая реактивную тягу и, с другой стороны, давит на жидкость, оставшуюся в начале конуса, выталкивая её обратно в насос и далее в теплообменник. При этом, в отличие от сопла, канал не является открытым объёмом, и испарение продолжается достаточно длительное время, по мере падения давления при выходе пара (через форсунки) и оставшейся жидкости (через насос и теплообменник). Поэтому в данном случае актуально учитывать долю испарившейся воды, указанную в таблице 1.3. При испарении отбирается тепло у конуса и у перегретой жидкости, в результате чего пара образуется меньше, чем при испарении в сопле, а его температура в канале не опускается ниже температуры кипения жидкости при атмосферном давлении.
По большому счёту, при внезапной остановке возможны две проблемы: срыв конуса с вала из-за сил инерции и повареждение насоса и теплообменника при обратном прорыве через них большого объёма жидкости и пара под высоким давлением. Защитой от этих неприятностей служит надёжное закрепление ротора на валу (либо конструктивно предусмотренная возможность его проворота при слишком большой нагрузке) и защита насоса и теплообменника от сильного обратного тока рабочего тела — специальной конструкцией насоса или установкой обратных и предохранительных клапанов.
Если остановка не была слишком длительной, то массивный конус может сохранить значительную часть тепла (возможно, некоторая часть его даже останется перегретой, так как пар у форсунок вытеснит жидкость, а сам не сможет отобрать у канала слишком много тепла). В этом случае повторный запуск двигателя будет лёгким и быстрым. Если теплоёмкость конуса мала, то повторный старт будет мало отличаться от «холодного» запуска.
Регулировка мощности
Для оперативной регулировки мощности помимо использования балластной нагрузки есть только один путь — управление потоком жидкости через конус. Обеспечить это можно с помощью заслонки, размещённой до насоса (на участке низкого давления) или после него перед конусом (участок высокого давления). Другой способ — частично или полностью отключать одну или несколько форсунок, когда полная мощность не требуется. Этот метод может быть даже более предпочтителен, поскольку практически не меняет общий температурный режим конуса, но зато само управление форсунками на быстро вращающемся конусе является нетривиальной инженерной задачей. Наконец третий вариант, предложенный Робертом Кунцем, — управление обратным подпором отработанной жидкости — я оцениваю как оригинальный, но на практике малопригодный. Он требует специальной конструкции и строго определённой компоновки двигателя.
В любом случае уменьшение общего потока снизит тягу, а увеличение — повысит. Однако здесь есть один нюанс — если снижение тяги присходит достаточно быстро, то её увеличение может зависеть не только от потока и его давления, но и от запасённой в конусе теплоты, а вот её-то в некоторых случаях после длительной работы на малых оборотах может и не хватить для полной тяги, а наращивание может потребовать заметного времени в силу известной инерционности тепловых процессов. Впрочем, имея в виду эту особенность, при создании конструкции, ориентированной на резкое изменение нагрузки, можно принять меры для её компенсации.
Выбор параметров конструкции
Разобравшись с общими принципами работы двигателя Клема, можно подумать и о конкретных конструкциях. Сразу скажу, что результаты будут несколько неожиданными, иногда прямо противополжными тому, что только что утверждалось чуть выше...
Но прежде всего необходимо определиться с выбором рабочего тела.
Вода, масло, спирт...
Если всё так хорошо с водой, почему Клем выбрал растительное масло? Как известно, масло практически не кипит, хотя при высоких температурах всё-таки немного испаряется. Вот эта-то слабая испаряемость масла и разрушает всю нашу красивую термодинамическую теорию! Но может быть, того, что испарялось, всё же хватало для работы? Ведь недаром же Клем вынужден был разогревать масло именно до 150°С, когда его испарение становится более-менее ощутимым?
Кроме того, у масла есть ещё один плюс — в отличии от большинства жидкостей с однородным химическим составом, при снижении температуры оно не переходит в твёрдое состояние, а постепенно повышает свою вязкость, с одной стороны, плавно замедляя работу механизма при излишнем адиабатическом охлаждении, а с другой, делая возможным его запуск при весьма низкой температуре окружающей среды.
Почему Клем не использовал воду? Как мы выяснили выше, в некоторых режимах работы, прежде всего при увеличении нагрузки (и, как предельный случай, при внезапной остановке), происходит несбалансированно большое увеличение парообразования, и соответственно, повышение давления внутри корпуса. Если при этом внутренний объём корпуса соединён с атмосферой (а это необходимо для предотвращения нежелательных эффектов при резком увеличении парообразования, проще говоря для того, чтобы двигатель не взорвался при резкой остановке), то излишки лёгкого водяного пара выходят в атмосферу гораздо активнее, чем относительно тяжёлые пары масла, которые достаточно просто улавливать и возвращать обратно (в двигателях внутреннего сгорания эта проблема решена десятки лет назад). Поэтому неудивительно, что вода очень быстро «выкипает». Кроме того, весьма низкая вязкость воды обеспечивает относительно небольшое жидкостное трение и, следовательно, затрудняет вызванный этим нагрев, требуя значительно большей длины спиральных каналов. Очевидно, по тем же причинам будет затруднено и использование других легкоиспаряющихся жидкостей с низкой вязкостью, таких как спирт или ацетон.
Тем не менее, в рамках термодинамической модели использование именно таких жидкостей представляется достаточно актуальным, поскольку парообразование у них намного эффективнее, чем у масла. Наибольший интерес представляет нетоксичный (если не отхлёбывать из двигателя!) и широко распространённый этиловый спирт (температура замерзания -114°С, кипения при атмосферном давлении +78°С, сжимаемость в два с лишним раза больше, чем у воды) или его аналоги. Проблему с «выкипанием» вполне можно решить с помощью конденсаторов паров в каналах, связывающих картер с атмосферой, либо вообще применить герметичный мембранный компенсатор давления (конечно, с предохранительным клапаном на случай аварии).
Первый расчёт элементов конструкции
Теперь можно попробовать уточнить данные конкретных элементов двигателя, параметры которого мы предварительно оговорили немного выше.
Сопло
В сопле происходит расширение пара от давления испарения до атмосферного давления. Соответственно, в оптимальном случае площадь сечения сопла от форсунки (наименьшее) до среза (наибольшее) должно изменяться в такое же число раз. Слишком малое расширение сопла уменьшит эффективность использование энергии образовавшегося пара, а слишком большое — вызовет разрежение за срезом сопла, тормозящее вращение. В нашем случае при рабочем давлении около 500 кПа следует выбирать соотношение сечений сопла у форсунки и среза (с небольшим запасом) 1:4.5 или даже 1:4, т.е. соотношение диаметров 1:2 или чуть больше.
Какую длину должно иметь сопло? С одной стороны, его сечение должно увеличиваться достаточно быстро, чтобы испаряющаяся жидкость не испытывала существенного давления со стороны ранее испарившихся её порций, т.е. скорость его расширения относительно вылетевшей из форсунки струи перегретой жидкости должна быть сравнима со скоростью теплового движения молекул пара (отличаться в разы, а не в сотни раз). С другой стороны, сопло не должно расширяться слишком быстро, чтобы сформировать направленную в желаемом направлении струю пара, поэтому скорость пролёта жидкости должна быть заметно (в несколько раз) меньше скорости теплового движения молекул. Выбрав компромиссное соотношение скоростей равным 10, и считая скорость истечения жидкости из сопла равной 33 м/с, а скорость теплового движения молекул порядка 500 м/с, получаем раскрытие сопла равным 500 / (33 · 10) = 1.51 = 151% по площади, что для линейных размеров соответствует 1.23 = 123%, т.е. на каждый сантиметр (метр, миллиметр — в зависимости от габаритов) длины его диаметр увеличивается в 1.23 раза.
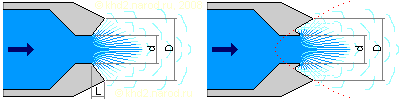 Сопло двигателя Клема для рабочего давления парообразования 4.5..5 атм. Соотношение диаметра форсунки d к диаметру среза сопла D 1:2 (расширение в пределах сопла в 4 раза). Слева — прямая коническая форма (раскрытие (D – d) / L = 123%), справа — параболическая (красным пунктиром показана образующая параболы).
Вероятно, дополнительно увеличить эффективность сопла можно, придав ему параболическую форму и разместив срез форсунки (точнее, точку максимального парообразования) в его фокусе. Здесь вычисленный ранее угол раскрытия не актуален, но соотношение диаметров форсунки и среза сопла остаётся в силе.
Конус
Теперь надо определить длину спирального канала и, следовательно, размеры конуса. Расчёт начнём с определения желаемой длительной мощности — предположим 1 кВт — и рабочего перепада температур в теплообменнике — заложим на это 10°, чтобы двигатель уверенно работал при температуре от +15°С и выше.
Теперь можно определить расход рабочего тела. При изменении температуры на 10° 1 кг (он же литр) воды получает немногим более 40 кДж тепла. Для обеспечения мощности в 1 кВт нужно ежесекундно расходовать всего 1 кДж энергии, таким образом 1 кг воды должен проходить через форсунки за 40 секунд. Отсюда следует, что скорость расхода рабочей жидкости можно вычислить по формуле
где N — желаемая мощность в долговременном режиме; c — удельная теплоёмкость рабочего тела в жидкой фазе в диапазоне от температуры окончания адиабатического расширения до температуры окружающей среды, соответствующего диапазону температур в теплообменике (следует выбирать наименьшее из значений теплоёмкости); δT — предполагаемая минимальная рабочая разность температур в теплообменнике.
Подставляя численные значения, получаем скорость расхода воды равной 1000 / (4190 · 10) = 0.024 кг / сек. Для удобства дальнейших расчётов немного округлим результат (естественно, в большую сторону) и будем считать расход равным 0.025 кг / сек.
Суммарное сечение всех спиральных каналов в конусе должно пропустить необходимое количество с расчётной скоростью.
где q — скорость массового расхода рабочего тела; ρ — удельная плотность рабочей жидкости (для канала постоянного сечения следует брать наименьшее значение плотности, соответствующее наибольшей температуре); vТ — скорость движения рабочей жидкости в спиральном канале.
Как мы вычислили выше, при соотношении площади форсунки к сечению трубки (спирального канала) 1:20 и выбранных нами скорости и радиусе вращения форсунок скорость рабочего тела в спиральном канале ротора составит чуть менее 1.7 м/с. Подставив в эту формулу численные значения с учётом удельной плотности воды при 150°С, равной 917 кг / м3, получим 0.025 / (917 · 1.7) = 16.0·10–6 м2 = 16.0 мм2. То есть, диаметр трубки спирали (в случае круглого сечения) должен быть не менее 4.5 мм, а диаметр форсунки при этом составит 0.23 мм — значения, прямо скажем, очень небольшие.
Теперь надо определить длину спирали. Как мы уже выяснили, тепла, выделившегося при прохождении рабочей жидкости по спирали, прежде всего за счёт трения, должно хватать на её нагрев до расчётной температуры возле форсунок, а расчёт следует проводить для установившегося длительного режима работы на расчётной мощности. Каковы потери на трение жидкости, которые и превратятся в тепло?
К сожалению, гидродинамические расчёты обычно сводят потери на трение не к нужным нам потерям энергии, а к потерям напора или, в лучшем случае, давления. Однако, потери напора и давления можно перевести в потери мощности.
Как известно, в трубе круглого сечения потери вычисляются по формуле Вейсбаха-Дарси, откуда необходимая длина спирального канала вычисляется как
l = 2 · d · g · HT / (λ · v2) = 2 · d · g · NT / (q · g · λ · v2) = 2 · d · NT / (q · λ · v2) (1.3),
где l — длина спирального канала; d — внутренний диаметр трубы; g — ускорение свободного падения; HT — потери напора на трение (высота столба жидкости, м); λ — безразмерный коэффициент жидкостного трения, зависящий от условий течения жидкости; v — средняя (измеренная по расходу) скорость жидкости в трубе; NT — мощность, расходуемая на жидкостное трение; q — массовый расход жидкости в трубе, кг / с.
Мощность потерь должна обеспечить нагрев жидкого рабочего тела на ΔT – δT — от его минимальной температуры в конце цикла расширения (0°C) до температуры перед форсункой (150°С) за вычетом минимального расчётного нагрева в теплообменнике (10°С). Эта мощность определяется теплоёмкостью рабочей жидкости и её массовым расходом NT = q · c · (ΔT – δT). Поэтому окончательная формула выглядит как
l = 2 · d · q · c · (ΔT – δT) / (q · λ · v2) = 2 · d · c · (ΔT – δT) / (λ · v2) (1.4),
где l — длина канала; d — его внутренний диаметр; q — массовый расход жидкости в трубе, кг / с; с — усреднённая удельная теплоёмкость рабочего тела в жидкой фазе в рабочем диапазоне температур; ΔT — максимальная разность температур рабочего тела (перед форсункой и при конденсации расширившегося пара); δT — предполагаемая минимальная рабочая разность температур в теплообменнике; λ — безразмерный коэффициент жидкостного трения, зависящий от условий течения жидкости; v — средняя (измеренная по расходу) скорость жидкости в трубе.
Вычислим коэффициент жидкостного трения. Для наших условий число Рейнольдса не превышает Re = 1.7 · 0.0045 · 1000 / 2·10-3 = 3825, а то и вдвое меньше. Поэтому будем считать течение ламинарным. Отсюда следует, что коэффициент жидкостного трения надо вычислять как λ = 64 / Re, а необходимую длину канала для ламинарного потока надо рассчитывать как
l = d · c · (ΔT – δT) · Re / (32 · v2) (1.5).
Подставляя конкретные цифры, получаем минимальную длину канала равной l = 0.0045 · 4190 · (150 - 10) · 3825 / (32 · 1.72) = 109 179 м. Да уж, перспектива мотать больше сотни километров трубки сразу отбивает желание воплощать такую «перспективную идею» в натуре. Однако посмотрим на формулу повнимательнее, и подумаем, как сократить это число? Обратившись к более общей формуле (1.4), мы видим, что для этого прежде всего можно увеличить скорость (как-никак, вторая степень), уменьшить диаметр канала (кстати, при том же расходе уменьшение диаметра автоматически влечёт повышение скорости, и наоборот), и увеличить коэффициент жидкостного трения, который существенно возрастает при переходе потока в категорию турбулентных, то есть и в этом случае опять-таки необходимо повысить скорость, но сохранить диаметр, а значит, надо увеличить расход. Термодинамические параметры — теплоёмкость и диапазон температур — определяются выбранным рабочим телом, и изменить их мы можем, лишь выбрав другое рабочее тело. Однако пока попробуем «выжать» максимум из обыкновенной воды. Впрочем, мы всё-таки можем выбрать более низкую температуру в форсунке, но снижение разности температур ведёт к понижению давления парообразования в сопле и снижению тяги, производимой образовавшимся паром — ведь в этой части мы имеем дело с классической тепловой машиной, — так что температуру лучше не снижать.
Кстати, поток в спиральном канале насоса-прототипа безусловно, является турбулентным. Более того, сама конструкция этого канала, стенки которого образуются проточкой ротора и внутренней поверхностью корпуса, движутся относительно потока в разные стороны, дополнительно завихряя его и повышая его естественную турбулентность!
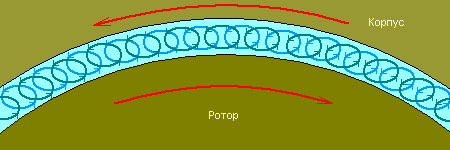 Дополнительное завихрение жидкости в канале конического насоса-прототипа за счёт встречного движения стенок (скорости показаны относительно усреднённой скорости потока жидкости).
Итак, первая попытка расчёта принесла очень интересные результаты, которые можно свести к необходимости обеспечения максимальной скорости и турбулентности потока в спиральном канале ротора. Из этого следует, что в канале нужно убрать искусственное препятствие в виде узкой форсунки на его конце. Что же обеспечит необходимое сопротивление движению потока, чтобы создать давление, нужное для поддержания перегретого рабочего тела в жидком состоянии? Только гидродинамическое сопротивление, вызванное жидкостным трением (вспомним фразу в описании насоса-прототипа, что весь спиральный канал можно рассматривать «как очень длинное сопло»). Впрочем, не всё так просто, и, чтобы разобраться в деталях, необходимо подробно рассмотреть, как изменяются условия в канале на протяжении его длины, и прежде всего это касается давления.
Как поддержать давление?
Рассчитывая давление в спиральном канале, будем по-прежнему рассматривать канал круглого сечения с неподвижными стенками.
Очевидно, что при движении жидкости по каналу неизменного сечения и, следовательно, в силу уравнения непрерывности, с неизменной скоростью, жидкостное трение будет вызывать потерю напора или, другими словами, потерю давления по мере продвижения жидкости от входа в трубу к её выходу. Поэтому в случае горизонтальной трубы для обеспечения нужной скорости свободно изливающегося потока на входе трубы необходимо создать избыточное давление, компенсирующее потерю напора при движении жидкости по этой трубе с заданной скоростью. Сразу возникает вопрос: а нельзя ли создавать это самое давление по мере продвижения жидкости по трубе, то есть компенсировать потери давления, так сказать, на ходу? Ответ: можно, если жидкость в этой трубе будет испытывать постоянное или периодическое воздействие каких-либо сил. Если разместить трубу вертикально, то такой силой может быть сила тяжести, а для свёрнутой в спираль вращающейся трубы это будет центробежная сила. Сразу хочу ещё раз подчеркнуть — наша цель заключается не в механическом разгоне потока, поскольку в замкнутом цикле это не может дать прибавки энергии, а в поддержании (или создании) нужного давления и разогреве потока до необходимой температуры. Сама по себе скорость потока для нас не имеет значения, кроме обеспечения жидкостного сопротивления, необходимого для достижения этих двух целей!
Отсюда следует, что, во-первых, на каждом участке трубки прибавка давления от действия центробежных сил должна превышать потери давления от жидкостного трения
Во-вторых, как мы уже говорили выше, энергия, потраченная на жидкостное трение (плюс неизбежные потери на теплообмен с внешней средой через стенки трубки), должна быть достаточной для нагрева жидкости до необходимой нам температуры, откуда следует условие
PT · qV ≥ ΔT · q · c (2.2),
где PT — общая потеря давления из-за жидкостного трения при прохождении жидкости по всей длине трубки; qV — объёмный расход жидкости, м3/ с; ΔT — необходимый нагрев жидкости (разность температур); q — массовый расход жидкости в трубе, кг / с; c — усреднённая (в диапазоне температур нагрева) теплоёмкость рабочего тела в жидком состоянии.
Выразив объёмный расход через массовый, мы приходим к соотношению
где PT — общая потеря давления из-за жидкостного трения при прохождении жидкости по всей длине трубки; ΔT — необходимый нагрев жидкости (разность температур); c — усреднённая (в диапазоне температур нагрева) теплоёмкость рабочего тела в жидком состоянии; ρ — усреднённая (в диапазоне температур нагрева) плотность рабочего тела в жидком состоянии.
Давление от действия центробежных сил можно вычислить как
PЦ = m · (aЦС – aЦИ) / S = l · S · ρ · (aЦС – aЦИ) / S = l · ρ · (aЦС – aЦИ) (2.4),
где PЦ — общая прибавка давления от действия центробежных сил при прохождении жидкости по всей длине трубки; m — масса жидкости в трубке; aЦС и aЦИ — центростремительное ускорение в точках стока (выхода из трубки) и истока (входа в трубку) соответственно; l — длина трубки; S — площадь сечения трубки (неизменная по всей её длине); ρ — усреднённая плотность рабочей жидкости; f — частота вращения ротора; RС и RИ — радиусы вращения точек стока и истока соответственно.
В нашем случае жидкость движется по спирали, при этом её скорость практически на всём протяжении спирали при неизменном сечении канала относительно его стенок будет одинаковой. В связи с этим разность давлений для открытого канала с учётом определения тангенциальной скорости ротора через скорость его вращения следует записать как
PЦ = l · ρ · ((2 · π · f · RC – v)2 / RC – (2 · π · f · RИ – v)2 / RИ) = l · ρ · ((2 · π · f)2 · (RC – RИ) + v2 / RС – v2 / RИ) (2.5),
где PЦ — общая прибавка давления от действия центробежных сил при прохождении жидкости по всей длине трубки; l — длина трубки; ρ — усреднённая плотность рабочей жидкости; f — частота вращения ротора; RС и RИ — радиусы вращения точек стока и истока соответственно; v — скорость течения жидкости в спиральной трубке относительно её стенок. Следует заметить, что при уменьшении радиусов прибавка давления стремится к бесконечности, но физического смысла это не имеет — даже при подаче жидкости через середину вала ротора в качестве входного радиуса следует брать радиус отверстия, через которое жидкость поступает в ротор, поэтому RИ никогда не может быть бесконечно малым, а RС у нас всегда должен быть больше RИ.
На основании соотношений (2.1), (2.3) и (2.5) можно определить первый критерий минимальной длины спирального канала:
l ≥ ΔT · c / ((2 · π · f)2 · (RC – RИ) + v2 / RС – v2 / RИ) (2.6).
Здесь равенство соответствует обеспечению минимального нагрева при условии отсутствия теплопотерь и сохранении давления неизменным. Увеличение длины сверх минимальной позволит получить больший нагрев. Следует заметить, что при уменьшении частоты вращения f или увеличении скорости в канале v значение l нарастает сначала медленно, а затем всё быстрее, и вдруг становится сильно отрицательным. Отрицательные значения соответствуют ситуации, когда на большей части радиуса жидкость в канале движется в сторону, противоположную вращению ротора — не только относительно стенок канала, но и относительно внешнего наблюдателя, находящегося вне двигателя в инерциальной системе отсчёта, то есть центробежные силы будут не столько ускорять, сколько тормозить жидкость. Однако центробежным силам, а стало быть и вызванному ими давлению, безразлично, в какую сторону происходит вращение — главное, чтобы оно происходило. Поэтому формулу (2.6) следует записать в виде
l ≥ ΔT · c / ((2 · π · f)2 · (RC – RИ) + |v2 / RС – v2 / RИ|) (2.7),
где вертикальные палочки | обозначают абсолютную величину (модуль) выражения, заключённого в них.
Однако следует помнить, что в тех случаях, когда формула (2.6) даёт отрицательные значения, режим двигателя абсолютно не соответствует расчётному, суммарная работа центробежных сил способствует торможению жидкости относительно стенок канала, а не её разгону, и это требует создания существенно большего давления на входе и, соответственно, затрат мощности на это. В результате на основании формул (2.6) и (2.7) приходим к выводу, что для поддержания и наращивания давления было бы желательно обеспечить минимальную скорость потока и максимальную скорость вращения ротора (центробежную силу). Впрочем, это следует и из уравнения Бернулли, которое однозначно говорит об обратной зависимости между квадратом скорости потока и его давлением. Тем не менее, из формулы (2.7) следует и ещё один вывод — высокого центробежного давления можно достичь и в неподвижном роторе, обеспечив высокую скорость потока в спиральном канале. Правда, при этом не совсем ясно, как же снимать мощность с такого потока — ведь в этом случае спираль будет неподвижной!
В заключение этого пункта приведу таблицы для различных скоростей вращения ротора и потока в канале в случае нагрева воды с 0 до 150°С в жидком состоянии. Красным цветом выделены сочетания условий, где суммарное действие центробежных сил тормозит поток относительно стенок канала, зелёным — ускоряет.
Таблица 2.1. Минимальная длина спирального канала для нагрева воды на 150°С при разных скоростях потока и вращения ротора для радиуса выхода 15 см и входа 1 см
Скорость вращения →
Скорость потока ↓ |
0 об/с (ротор стоит) |
10 об/с
(600 об/мин) |
20 об/с
(1200 об/мин) |
30 об/с
(1800 об/мин) |
40 об/с
(2400 об/мин) |
50 об/с
(3000 об/мин) |
| 0 м/с (канал заперт) |
- |
1137 м |
284.3 м |
126.4 м |
71.1 м |
45.5 м |
| 1 м/с |
6734 м |
979.9 м |
272.8 м |
124.0 м |
70.3 м |
45.2 м |
| 2 м/с |
1684 м |
678.7 м |
243.2 м |
117.5 м |
68.2 м |
44.3 м |
| 3 м/с |
748.2 м |
451.3 м |
206.0 м |
108.1 м |
64.9 м |
42.9 м |
| 5 м/с |
269.4 м |
217.8 м |
138.3 м |
86.0 м |
56.2 м |
38.9 м |
| 7 м/с |
137.4 м |
122.6 м |
92.6 м |
65.8 м |
46.8 м |
34.2 м |
| 10 м/с |
67.4 м |
63.6 м |
54.4 м |
43.9 м |
34.6 м |
27.2 м |
| 15 м/с |
29.9 м |
29.2 м |
27.1 м |
24.2 м |
21.1 м |
18.1 м |
| 20 м/с |
16.8 м |
16.6 м |
15.9 м |
14.9 м |
13.6 м |
12.3 м |
Таблица 2.2. Минимальная длина спирального канала для нагрева воды на 150°С при разных скоростях потока и вращения ротора для радиуса выхода 25 см и входа 1 см
Скорость вращения →
Скорость потока ↓ |
0 об/с (ротор стоит) |
10 об/с
(600 об/мин) |
20 об/с
(1200 об/мин) |
30 об/с
(1800 об/мин) |
40 об/с
(2400 об/мин) |
50 об/с
(3000 об/мин) |
| 0 м/с (канал заперт) |
- |
663.3 м |
165.8 м |
73.7 м |
41.5 м |
26.5 м |
| 1 м/с |
6546 м |
602.3 м |
160.7 м |
72.9 м |
41.2 м |
26.4 м |
| 2 м/с |
1636 м |
472.0 м |
150.6 м |
70.6 м |
40.4 м |
26.1 м |
| 3 м/с |
727.4 м |
347.0 м |
135.1 м |
66.9 м |
39.2 м |
25.6 м |
| 5 м/с |
261.9 м |
187.8 м |
101.5 м |
57.5 м |
35.8 м |
24.1 м |
| 7 м/с |
133.6 м |
111.2 м |
74.0 м |
47.5 м |
31.6 м |
22.1 м |
| 10 м/с |
65.5 м |
59.6 м |
46.9 м |
34.6 м |
25.4 м |
18.9 м |
| 15 м/с |
29.1 м |
27.9 м |
24.8 м |
20.9 м |
17.1 м |
13.9 м |
| 20 м/с |
16.4 м |
16.0 м |
14.9 м |
13.4 м |
11.7 м |
10.1 м |
Можно заметить, что при малых скоростях вращения и высоких скоростях потока диаметр ротора практически не имеет значения — всё определяет скорость потока и длина канала, поэтому даже разница между конической и цилиндрической навивками спирали будет невелика (правый нижний угол таблиц). При высоких скоростях вращения и относительно низкой скорости потока, наоборот, всё опеределяет диаметр ротора (левый верхний угол таблиц). При этом по мере роста диаметра ротора длина канала, наоборот, сокращается, поэтому после некоторого предела возможна упаковка канала не в коническую, а в плоскую спираль — правда, если при этом длины спирали будет достаточно для обеспечения необходимых потерь на трение.
В завершение надо добавить, что канал может иметь и меньшую длину, но в этом случае будет иметь место потеря давления, то есть при обеспечении необходимых для нужного нагрева потерь на жидкостное трение, давление на его выходе будет меньше давления на входе.
Как увеличить потери?
Как мы уже выяснили, чтобы уменьшить длину канала до более-менее приемлемых габаритов, нам необходимо как можно больше увеличить потери на жидкостное трение. Прямо скажем, задача необычная, ведь практически всегда эти потери требуется снизить!
Чуть выше в формуле (2.3) мы вывели зависимость потерь давления на трение от необходимого нам нагрева за счёт этих потерь. Переводя давление в привычный для гидродинамических расчётов напор, мы получим минимально необходимые потери напора от жидкостного трения
HT = PT / (g · ρ) = ΔT · c / g (3.1),
где HT — необходимые потери напора на трение; PT — необходимые потери давления на трение; g — ускорение свободного падения; ρ — усреднённая плотность рабочей жидкости в диапазоне температур нагрева; ΔT — необходимая разность температур; с — усреднённая теплоёмкость рабочей жидкости в диапазоне температур нагрева.
Для нагрева воды на 150°С эти потери составят примерно HТв = 150 · 4190 / 9.81 ~ 64 км (да-да, именно километров!), что соответствует потере давления в 6.3·109 Па (6200 атм). Неудивительно, что мало кому придёт в голову разогревать воду за счёт жидкостного трения — подобные цифры сразу относят эту идею в разряд ненаучной околотехнической фантастики! Для масла, обладающего меньшими плотностью и теплоёмкостью, чем вода, цифры будут в 3..5 раз меньше, но и это очень немало!
Гладкая труба
И всё же попробуем (хотя бы теоретически) рассчитать параметры потока для достижения подобных потерь. Для начала предположим, что мы имеем дело с сильно турбулентным потоком в гидравлически гладкой трубе. В таком случае в соответствии с формулой Вейсбаха-Дарси и числом Рейнольдса потери напора определяются как
HT = (0.3164 / Re0.25) · (l / d) · v2 / (2 · g) = (0.3164 / (v · d · ρ / η)0.25) · (l / d) · v2 / (2 · g) (3.2),
где HT — потери напора на трение; Re — число Рейнольдса; l — длина трубы; d — её диаметр; v — усреднённая скорость потока (вычисляемая по расходу); g — ускорение свободного падения; ρ — усреднённая плотность рабочей жидкости в диапазоне температур нагрева; η — усреднённая динамическая вязкость рабочей жидкости в диапазоне температур нагрева.
Отсюда минимально необходимую длину канала можно вычислить по формуле
l = HT · (v · d · ρ / η)0.25 · 2 · g · d / (0.3164 · v2) (3.3).
Результаты расчёта для нескольких скоростей и диаметров канала сведём в таблицу (красным показаны сочетания параметров, соответствующие ламинарному течению потока, поэтому указанные в таблице значения могут быть сильно занижены).
Таблица 3.1. Минимальная длина спирального канала для обеспечения гидравлических потерь, необходимых для нагрева воды на 150°С при разных скоростях потока и диаметрах канала
Диаметр канала d →
Скорость потока v ↓ |
1 мм |
4 мм
(1/6") |
8 мм
(1/3") |
12 мм
(1/2") |
19 мм
(3/4") |
25 мм
(1") |
| 0.1 м/с |
1274 км |
7210 км |
17149 км |
28468 км |
50561 км |
71252 км |
| 1 м/с |
22.66 км |
128.2 км |
305.0 км |
506.2 км |
899.1 км |
1267 км |
| 2 м/с |
6739 м |
38.12 км |
90.66 км |
150.5 км |
267.3 км |
376.7 км |
| 3 м/с |
3315 м |
18.75 км |
44.59 км |
74.02 км |
131.5 км |
185.2 км |
| 5 м/с |
1355 м |
7669 м |
18.24 км |
30.28 км |
53.78 км |
75.79 км |
| 7 м/с |
752.4 м |
4256 м |
10.12 км |
16.80 км |
29.85 км |
42.06 км |
| 10 м/с |
403.1 м |
2280 м |
5423 м |
9002 м |
15.99 км |
22.53 км |
| 15 м/с |
198.3 м |
1121 м |
2667 м |
4427 м |
7864 м |
11.08 км |
| 20 м/с |
119.8 м |
677.9 м |
1612 м |
2676 м |
4754 м |
6699 м |
Результаты не слишком утешительны, необходимая длина варьируется от тысяч километров до сотен метров, причём последние значения соответствуют мизерному диаметру и высокой скорости потока, а, стало быть, и высокому давлению. Однако, с ростом скорости необходимая длина сокращается почти обратно пропорционально квадрату скорости, а это значит, что основное внимание надо уделить именно повышению скорости. Кроме того, мы рассматривали вариант гидравлически гладкой трубы, а ведь на пути потока можно создать искусственные препятствия-завихрители. Удастся ли с их помощью сократить необходимую длину канала до разумных значений — максимум, несколько десятков метров?
Труба с перегородками
Рассматривая различные варианты завихрителей потока в трубе, я прихожу к выводу, что наиболее простым и технологичным решением является обеспечение резких расширений и сужений русла потока. Технически это можно реализовать, набив трубку попеременно втулками с большим и малым диаметром отверстий, как показано на рисунке. Втулки с малыми отверстиями будут соответствовать резким сужениям сечения, а втулки с большими отверстиями — играть роль проставок между ними и обеспечивать резкое расширение сечения. Проведём расчёт именно для этого простейшего случая, хотя, конечно, в реальности длину трубки можно использовать более эффективно.
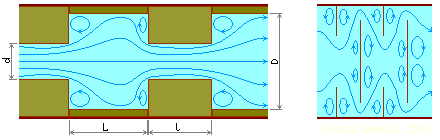
Канал с переменным сечением. Слева — рассчитываемый вариант, справа — вариант с завихрителями, использующими длину трубки более эффективно. D — диаметр большого сечения (во втулке-проставке), L — длина втулки-проставки, d — диаметр малого сечения (во втулке-жиклёре), l — длина втулки-жиклёра.
В нашем случае как единичный элемент следует рассматривать пару втулок и, следовательно, пару изменений профиля «сужение-расширение». При этом потери напора в каждой паре будут определяться по формуле
HП = (ζC + ζР) · v2 / (2 · g) = ((1 – SУ / SШ)2 + (1 – SУ / SШ) / 2) · v2 / (2 · g) = ((1 – (d / D)2)2 + (1 – (d / D)2) / 2) · v2 / (2 · g) (3.4),
где HT — потери напора; ζС — коэффициент потерь при сужении канала; ζР — коэффициент потерь при расширении канала; v — скорость в наименьшем сечении канала (наиболее высокая скорость); g — ускорение свободного падения; SУ — площадь сечения канала в узкой втулке; SШ — сечение канала в широкой втулке; d — диаметр узкого отверстия; D — диаметр широкого отверстия.
Соответственно, необходимое число элементов (пар втулок) рассчитывается по формуле
где n — число элементов; HT — общие необходимые потери напора; HП — потери напора на одном элементе (паре сужение-расширение канала).
Отметим интересный факт: в полученных формулах не фигурирует вязкость жидкости. Значит ли это, что необходимое число элементов будет одинаковым и для воды, и для масла? Конечно, нет! Оно зависит от необходимых потерь напора, а вот при их вычислении природа жидкости учитывается в полной мере!
Результаты расчёта для нескольких комбинаций параметров сведены в таблицу.
Таблица 3.2. Потери напора на одном элементе (паре сужение-расширение канала) и минимально необходимое число таких элементов (в скобках) для нагрева воды на 150°С при разных скоростях потока и различных соотношениях диаметров
широкой и узкой частей
Соотношение диаметров D / d →
Скорость потока v ↓ |
1.5 |
2 |
3 |
5 |
10 |
20 |
50 |
| 1 м/с |
30 мм (-) |
48 мм (-) |
63 мм (-) |
71 мм (-) |
75 мм (-) |
76 мм (-) |
76 мм (-) |
| 2 м/с |
0.119 м (-) |
0.191 м (-) |
0.252 м (-) |
0.286 м (-) |
0.301 м (-) |
0.305 м (-) |
0.306 м (-) |
| 3 м/с |
0.269 м (-) |
0.430 м (-) |
0.566 м (-) |
0.643 м (-) |
0.676 м (96062) |
0.685 м (94862) |
0.687 м (94530) |
| 5 м/с |
0.747 м (86989) |
1.19 м (54413) |
1.57 м (41320) |
1.79 м (36396) |
1.88 м (34582) |
1.90 м (34151) |
1.91 м (34031) |
| 7 м/с |
1.46 м (44383) |
2.34 м (27762) |
3.08 м (21082) |
3.50 м (18569) |
3.68 м (17643) |
3.73 м (17424) |
3.74 м (17363) |
| 10 м/с |
2.99 м (21748) |
4.78 м (13604) |
6.29 м (10330) |
7.14 м (9099) |
7.51 м (8646) |
7.61 м (8538) |
7.64 м (8508) |
| 15 м/с |
6.73 м (9666) |
10.8 м (6046) |
14.2 м (4592) |
16.1 м (4044) |
16.9 м (3843) |
17.1 м (3795) |
17.2 м (3782) |
| 20 м/с |
12.0 м (5437) |
19.1 м (3401) |
25.2 м (2583) |
28.6 м (2275) |
30.1 м (2162) |
30.4 м (2134) |
30.6 м (2127) |
Количество элементов в таблице указано лишь для тех сочетаний параметров, при которых оно не превышает 100 000, большие количества заменены прочерками (впрочем, для их вычисления достаточно поделить напор в 65 км на падение давления на одном элементе). В любом случае, даже при огромной скорости 20 м/с, количество элементов исчисляется тысячами, однако это не повод отказываться от этого способа увеличения потерь — ведь здесь мы не учитывали потери на «обычное» сопротивление потоку, рассчитанное в предыдущем пункте. Поэтому, рассматривая данный способ создания потерь в качестве дополнительного, можно оценить его как весьма эффективный и простой в реализации, и отметить ряд особенностей.
Во-первых, как и в случае прямого потока в гладкой трубе, потери резко возрастают с ростом скорости потока, причём зависмость эта не почти квадратичная, а строго квадратичная.
Во-вторых, не следует стремиться к наибольшей разности диаметров большого и малого сечений: если при их близких значениях увеличение разницы сечений существенно увеличивает потери, то затем это влияние уменьшается, и при соотношении диаметров широкой и узкой частей от 10:1 и более потери определяются уже практически лишь одной скоростью потока. Поэтому на практике стоит использовать разность диаметров каналов в диапазоне от 3:1 до 5:1 и не имеет никакого смысла стремиться к разности диаметров более 10:1, если только это не обусловлено какими-либо другими причинами.
Предварительные итоги=
Пытаясь рассматривать двигатель Клема как тепловую машину с точки зрения термодинамики, и предполагая, что энергия черпается в фазовых переходах из жидкости в пар и обратно, мы пока не получили готового рецепта по его изготовлению — данных по маслу недостаточно, а данные для воды требуют таких размеров устройства и скоростей движения жидкости, достичь нужного сочетания которых с технической точки зрения весьма непросто (правда, при этом рассматривалось течение жидкости в неподвижной трубке, а не в канале с неподвижной и движущейся стенками).
К тому же, похоже, предполагаемый тепловой баланс был рассчитан, исходя из излишне оптимистичных оценок парообразования, и требует слишком высокой эффективности преобразования тепловой энергии в механическую. В свете этого предположение о термодинамической природе работы двигателя Клема (как нарушение II начала термодинамики) представляется не соответствующим реальности — не потому, что II начало непререкаемо, а потому, что это не соответствует известным сведениям о двигателе Клема и не подтверждается расчётом (с учётом поправок на реальные потери и проблемы). Выбор Клемом в качестве рабочего тела практически не кипящего масла лишний раз подтверждает этот вывод.
Однако мы сумели прояснить многие интересные моменты в его конструкции и придти к некоторым выводам, актуальным и при конструировании других устройств, предназначенных для генерации дополнительной энергии в замкнутом цикле движения рабочей жидкости, в том числе аналогов генератора Потапова и установок «ЮСМАР».
Теперь понятно, почему...
Итак, теперь мы можем обосновать многие «странности» в описании и увидеть, что они совсем не случайны. Впрочем, в данный момент я считаю, что на самом деле большинство из них обусловлено совсем другими причинами, хотя они хорошо «ложатся» и в рассмотренную на данной странице гипотезу.
Малый вес обусловлен тем, что единственные крупные детали в двигателе — это сам конус и сопрягающийся с ним корпус, однако и их масса определяется только условием обеспечения достаточной прочности. Увеличение массы с целью повышения теплопроводности и / или теплоёмкости этих деталей не только не нужно, но и вредно! Объём рабочей жидкости должен быть достаточно большим, чтобы обеспечить не только заполнение спиральных каналов конуса и теплообменника, но и её достаточный запас в картере при высоком удельном расходе (большом потоке в рабочих каналах).
Высокая рабочая температура необходима для того, чтобы доля переходящей в перегретый пар рабочей жидкости была достаточной для обеспечения работоспособности установки.
Мощный насос необходим не столько для того, чтобы поддерживать достаточно высокое давление возле форсунок (при высоких скоростях вращения для этого может хватить и центробежных сил), а прежде всего для того, чтобы обеспечить высокую скорость потока в спиральном канале за счёт большого давления на его входе. Гидродинамические потери и вызванный ими нагрев практически обратно пропорциональны квадрату скорости потока, поэтому чем больше давление на входе спирального канала, тем более коротким каналом можно обойтись. Следует отметить, что вращающаяся спираль позволяет осуществить распределённую по всей длине компенсацию потерь напора и давления из-за гидродинамического трения за счёт центробежных сил, по крайней мере частично. Это позволяет заметно снизить давление на входе спирального канала по сравнению с неподвижным каналом с теми же гидродинамическими потерями и, соответственно, обеспечить более низкую и более равномерную нагрузку на стенки канала на всём его протяжении.
Проточка в теле конуса в сочетании с плотно прилегающим к конусу неподвижным корпусом (без их непосредственного соприкосновения!), как это имеет место насосе-прототипе, представляет собой завихритель, эффективность которого с точки зрения обеспечения удельных потерь и вызванного ими нагрева во много раз выше, чем у спиральной трубки с неподвижными стенками — а это позволяет существенно снизить длину канала и сократить габариты установки. Однако такое решение требует повышенной точности сопряжения и неизменности (или согласованного изменения) габаритов обоих сопрягающихся деталей в широком диапазоне температур и нагрузок, что, в свою очередь, приводит к необходимости обеспечения их повышенной прочности, а значит, и обуславливает существенную массу ротора и корпуса.
Поскольку основной результат прохождения жидкости по каналу — это её нагрев, то длина канала не может быть слишком маленькой, а диаметр ротора нельзя сделать слишком большим из технических соображений. Поэтому спираль заданной длины и заданного максимального радиуса приходится упаковывать в конус, хотя, если удастся сократить длину спирали ещё более, её можно будет упаковать в уплощённый конус или вообще в плоскую спираль. Возможно, именно это удалось Клему в последней модели его двигателя, однако скорее всего, при его создании он руководствовался совсем другими принципами.
«Размер имеет значение» и другие выводы
В результате проведённого анализа мы получили не только объяснение практически всех особенностей конструкции, но и можем сделать некоторые выводы.
Во-первых, двигатель не может быть слишком маленьких размеров. Хотя уменьшение диаметра канала и уменьшает его минимальную длину для достижения необходимых потерь напора и вызванного ими нагрева, при слишком маленьких размерах канала становится существенным влияние сил смачивания. Кроме того, при малых диаметрах ротора вклад центробежных сил становится несущественным, и практически всё необходимое давление придётся создавать насосом; вращающий момент реактивной струи из сопла также уменьшается пропорционально диаметру ротора. Так что создание сверхкомпактных двигателей Клема с габаритами в пару сантиметров не представляется возможным. А вот диаметром метр-другой — вполне возможно, если хватит запаса прочности материалов.
Во-вторых, гидродинамические потери, а стало быть, необходимая длина канала, помимо прочих факторов в значительной определяются вязкостью рабочей жидкости. И в этом плане выбор в качестве рабочей жидкости масла, как жидкости весьма вязкой, полностью оправдан. Однако даже сильно нагретое масло испаряется довольно слабо, и доля его паров относительно общей массы весьма мала. Поэтому вряд ли можно говорить о возможности падения температуры масла ниже температуры окружающей среды и, следовательно, о холодном теплообменнике! Так что сведения о горячем теплообменнике кажутся вполне оправданными, а это предполагает совсем другую причину работы двигателя Клема, нежели использование теплоты окружающей среды, то есть термодинамические процессы играют здесь лишь второстепенную роль.
♦
|