Кое-что из курса механики
Прежде чем идти дальше, я предлагаю немного освежить в памяти те сведения из механики, которые нам понадобятся. Здесь нет ничего, выходящего за рамки школьного курса (даже вместо интегрирования вполне достаточно использовать «суммирование по маленьким кусочкам»). Поэтому те, кто ещё не забыл про понятия силы, момента сил и работы, могут пропустить этот раздел и двигаться дальше. Основные механические величины и связывающие их формулы приведены в справочной информации. Там же сформулированы некоторые законы механики, которые необходимого учитывать не только при конструировании «мельниц» — тихоходных колёс, использующих гравитационное поле, — но и многих других типов устройств, где в той или иной форме используется механическое движение элементов конструкции. А на этой странице я хочу напомнить несколько нюансов, которые играют важную роль в понимании механического взаимодействия физических тел.
О физическом смысле
Представление о центре масс тела
Что такое вес
Представление о моменте силы и вращающий момент
Правило моментов и закон рычага
Понятие об устойчивом и неустойчивом равновесии и потенциальном барьере
Изменение давления с глубиной
Эффект Архимеда и его особенности
Справедливость законов классической механики
О физическом смысле
В отличии от «абстрактной» математики на каждом этапе физических расчётов необходимо чётко понимать их физический смысл и контролировать соответствие ему промежуточных и окончательных результатов. Например, для геометрических параметров и массы (не путать с весом!) отрицательные значения считаются не имеющими физического смысла, поскольку в реальном мире не встречаются, и их получение в результате расчётов однозначно свидетельствует о каких-то ошибках либо в самих вычислениях, либо немного раньше — в умозаключениях, на основе которых эти вычисления проводились.
Тем не менее, получение «нереальных» результатов отнюдь не всегда говорит об ошибке в расчёте. Иногда это лишь признак того, что физическое явление переходит в новую качественную стадию. Например, при гидравлических расчётах вполне возможно получить отрицательное давление — давление меньше абсолютного нуля, то есть вакуума. В реальности такого, естественно, быть не может, однако на самом деле это означает лишь переход процесса в другое качество — в данном случае речь идёт о возникновении интенсивных кавитационных процессов. Впрочем, всё равно для такого случая необходимо применять другой расчёт, нежели для потока без кавитации — явное или неявное исходное предположение об отсутствии кавитации было неверным...
Представление о центре масс тела
Прежде всего следует напомнить, что очень часто в механике рассматривается движение и взаимодействие не самих тел, имеющих ту или иную конкретную форму, а их центров масс — физической абстракции, предполагающей, что вся масса тела сосредоточена в некоторой его точке, которая для однородного тела совпадает с его геометрическим центром. Во многих случаях это позволяет упростить используемые физические модели и соответствующие расчёты. В общем случае, рассматривать систему тел как точечное тело, находящееся в центре масс этой системы, допустимо лишь тогда, когда воздействие на всю рассматриваемую конфигурацию можно считать однородным в пределах её границ (например, гравитационное поле на поверхности Земли, атмосферное давление, в некоторых случаях — давление жидкости и т.п.), а также если воздействие является точечным, но направлено точно в центр масс жёсткого тела или жёсткой системы тел. Наиболее полно удовлетворяют этому условию жёсткие шарообразные тела, однако даже они при реальных столкновениях как между собой, так и с плоскими поверхностями в случае «скользящего» удара могут закручиваться, на что будет использована часть энергии, которой они обладали до столкновения (с точки зрения перемещения центра масс такого шара эта часть энергии будет «потеряна»).
Тем не менее, довольно часто положение центра масс фигуры, тела или системы тел при рассмотрении их в качестве «точечного тела» определяет место, которое можно рассматривать как точку приложения силы, действующей на эту фигуру, тело или систему тел как на единое целое. Такой подход неприменим в тех случаях, когда форма тела играет существенную роль — например, если одно тело ударяет в край другого. Впрочем, и в этих случаях зачастую удаётся мысленно разбить реальное тело на несколько частей таким образом, чтобы можно было работать с центрами масс этих частей, как автономных тел, и избежать необходимости интегрирования воздействия по всему объёму или поверхности тела, заменив его простым суммированием.
|
Фигура, тело
|
Положение центра масс
|
|
Отрезок прямой.
|
Посередине.
|
|
Прямоугольный треугольник.
|
Ортогональная проекция центра масс на каждый катет лежит на расстоянии 1/3 от прямого угла.
|
|
Произвольный треугольник.
|
Центр масс лежит на пересечении медиан, т.е. на расстоянии 1/3 высоты, построенной к любому основанию.
|
|
Прямоугольник, параллепипед.
|
Центр масс лежит в геометрическом центре, его ортогональная проекция находится посередине любой стороны или грани.
|
|
Окружность, круг, сфера, шар.
|
Центр масс лежит в геометрическом центре.
|
|
Произвольная система из n точечных тел с координатами xi, yi, zi и массами mi.
|
xцм = (m1· x1+ m2· x2 + ... + mn· xn) / (m1+ m2 + ... + mn)
yцм = (m1· y1+ m2· y2 + ... + mn· yn) / (m1+ m2 + ... + mn)
zцм = (m1· z1+ m2· z2 + ... + mn· zn) / (m1+ m2 + ... + mn)
|
Поскольку именно масса является мерой инертности тела, то выражения «центр масс тела» и «центр инерции тела» абсолютно равнозначны.
Что такое вес
Немаловажно помнить, что вес в килограммах меряют только в магазине! В физике в килограммах измеряют массу — меру инертности тела, а вес — это сила, с которой тело действует на опору в потенциальном гравитационном поле по направлению к центру этого поля. Из этого следует, во-первых, что в физике вес, как и любая другая сила, измеряется в ньютонах, а во-вторых, что в зависимости от окружающих условий, одно и то же тело может иметь как положительный, так и отрицательный вес. Классический пример — кусок дерева: в вакууме (и в воздухе, как среде с малой плотностью), он давит на опору в направлении силы тяжести с силой, пропорциональной его массе, т.е. имеет положительный вес; если же его погрузить в воду, имеющую более высокую плотность, чем он сам, то этот же кусок дерева приобретёт отрицательный вес, — будучи прикреплённым к опоре, он уже не давит на неё, а наоборот, пытается утащить её за собой против силы тяжести, и, если вес этой опоры достаточно мал, то всплывёт вместе с ней! При этом масса куска дерева в обоих случаях остаётся одной и той же.
Если плотность тела много больше плотности окружающей среды (т.е. для всех тел в вакууме и большинства тел в воздухе), то вес тела можно рассчитать по формуле
F = m · g (1),
Представление о моменте силы и вращающий момент
Поскольку работа практически всех «вечных мельниц» основана на разности моментов сил, этот момент следует осветить подробнее (нечаянный каламбур!). Будем рассматривать момент силы как меру поворачивающего воздействия на рычаг, один конец которого закреплён на оси (шарнире), а к другому приложена сила. Момент пропорционален величине силы и плечу рычага (расстоянию между центром поворота и точкой приложения силы), он стремится повернуть рычаг в ту же сторону, куда действует приложенная сила. Возьмём идеальный рычаг (тонкий, невесомо лёгкий и негнущийся), расположим его горизонтально, закрепим один конец в шарнире и на расстоянии, равном 1/3 от длины рычага подставим под него контрольную опору, силу давления рычага на которую будем измерять. Затем разместим груз точно над контрольной опорой, и измерим силу, с которой рычаг давит на опору. Потом переместим груз на свободный конец рычага, втрое дальше от шарнира, и вновь измерим силу давления на контрольную опору.
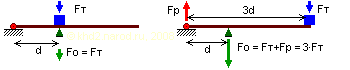 FT FT — вес груза, FO — сила, с которой рычаг воздействует на контрольную опору, FP — сила реакции шарнира, d — расстояние от шарнира (оси поворота) до точки измерения воздействия рычага (контрольной опоры).
Мы увидим, что во втором случае сила, действующая на контрольную опору, втрое больше, чем в первом. Откуда взялась добавка? Она появилась от того, что второй конец рычага закреплён в шарнире и не позволяет рычагу опрокинуться, как это случилось бы, если бы этот конец был свободным. Вот эта сила реакции шарнира и увеличила силу, действующую на контрольную опору (в первом случае реакция шарнира отсутствовала, т.к. весь вес груза приходился точно на нашу опору). Обратите внимание, что сумма всех сил осталась прежней. С точки зрения моментов силы мы можем сказать, что поскольку плечо увеличилось втрое, момент силы, действующий на рычаг, также увеличился втрое, и утроившаяся сила воздействия на контрольную опору это подтверждает. При этом можно не заморачиваться с учётом реакции опоры и т.д. Очевидно, что если на том же расстоянии от шарнира приложить бóльшую силу (например, разместить груз вдвое большей массы), то сила, действующая на контрольную опору, а стало быть, вращающий момент, то есть момент силы, стремящийся повернуть рычаг, увеличится ровно во столько же раз (для нашего примера — удвоится).
Поскольку предполагается, что в гравитационном двигателе работает сила тяжести, то очевидно, что в нормальных условиях (при небольших расстояниях и вблизи поверхности Земли) она практически постоянна и направлена всегда в одну и ту же сторону, соответственно и вес тела — проявление взаимодействия его массы с гравитационным полем — также постоянен и действует в одну и ту же сторону. В то же время, при вращении в вертикальной плоскости вокруг шарнира жёсткого рычага, на котором закреплено это тело, рычаг всё время меняет свой угол относительно силы тяжести. Возникает вопрос: каким образом зависит вращающий момент от угла поворота рычага?
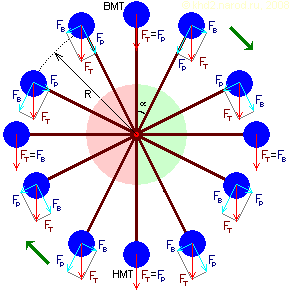 FT FT — вес груза, FP — сила, с которой рычаг воздействует на шарнир (компенсируется силой реакции опоры шарнира благодаря жёсткости рычага), FВ — нескомпенсированная поворачивающая сила, R — расстояние от шарнира (оси поворота) до траектории центра масс груза. Зелёным показана область ускорения, а красным — торможения груза.
Когда рычаг стоит строго вертикально вверх, весь вес груза передаётся на шарнир и, благодаря жёскости рычага, компенсируется реакцией опоры. Здесь вся сила направлена по нормали (т.е. перпендикулярно) к окружности, которую может описывать груз при вращении на рычаге вокруг шарнира. Тангенциальная составляющая силы, которая направлена вдоль окружности и может инициировать вращение рычага, полностью отсутствует, — соответственно, вращающий момент равен нулю. Это положение называется верхней мёртвой точкой (ВМТ).
Если начать отклонять рычаг с грузом от строго вертикального положения, реакция опоры уже не будет компенсировать весь вес груза, в результате появится тангенциальная (вращающая) составляющая силы, а нормальная (компенсирующая вес) составляющая начнёт уменьшаться. По мере увеличения отклонения рычага от вертикали тангенциальная (вращающая) сила будет нарастать, а нормальная (компенсирующая) — уменьшаться. Так будет продолжаться до тех пор, пока рычаг не примет горизонтальное положение.
Здесь нормальная сила будет равна нулю, а тангенциальная (вращающая) — полному весу груза, и вращающий момент будет максимальным. Затем рычаг снова начнёт действовать на груз, не давая ему удалиться от центра вращения, при этом груз уже будет пытаться не сжать, а растянуть рычаг — нормальная сила поменяет свой знак относительно рычага. Тангенциальная (вращающая) сила начнёт уменьшаться, а с ней начнёт уменьшаться и вращающий момент. Однако это не значит, что груз начнёт замедляться, ведь знак тангенциальной силы не изменился, — груз продолжит ускоряться, просто будет делать это не так резво, как в момент прохождения горизонтального положения. Так будет продолжаться до тех пор, пока рычаг не окажется в положении вертикально вниз, а груз не достигнет нижней точки своей траектории.
В этот момент весь вес опять будет полностью компенсирован нормальной силой, а тангенциальная составляющая уменьшится до нуля. Это положение называется нижней мёртвой точкой (НМТ). Здесь груз имеет максимальную скорость и кинетическую энергию. После прохождения этой точки тангенциальная составляющая снова появится, но уже с другим знаком — теперь вращающий момент также изменит знак, груз начнёт замедляться и набирать высоту, переводя свою кинетическую энергию в потенциальную и вновь возвращаясь к ВМТ. Однако это ему удастся только в двух случаях — либо шарнир был идеальным (абсолютно без трения) и отсутствовало сопротивление среды, либо грузу каким-либо образом была добавлена дополнительная энергия, достаточная, чтобы компенсировать потери на трение.
Математически зависимость вращающего момента от угла поворота для жёсткого невесомо лёгкого рычага, один конец которого закреплён на оси, а к другому прикреплён груз, при вращении в вертикальной плоскости в гравитационном поле описывается следующей формулой:
M = m · g · R · sin(α) (2),
где M — вращающий момент, вызванный грузом, m — масса груза, g — ускорение свободного падения (для поверхности Земли ~9.81 м/с2), R — расстояние от центра вращения до центра масс груза, α — угол отклонения от положения «вертикально вверх».
Правило моментов и закон рычага
Одним из основных правил, о котором ни в коем случае нельзя забывать при конструировании механических вечных двигателей, является правило моментов, которое гласит: моменты сил на обоих плечах рычага, закреплённого на оси и находящегося в покое, всегда взаимно скомпенсированы. Под «плечом» понимается расстояние от оси поворота до того места, к которому приложена сила. При этом если оба плеча находятся с одной стороны от оси, то направления моментов совпадают, а если с разных — противоположны. Если же векторная сумма моментов будет отлична от нуля, то рычаг начнёт ускоряющееся вращение в направлении большего из них (в случае, когда рычаг уже вращается и нескомпенисрованный момент сил действует против этого вращения, то вращение, наоборот, будет замедляться).
Поскольку момент силы равен произведению силы на длину плеча, из этого правила следует, что если рычаг используется для увеличения (уменьшения) силы на рабочем плече, то для перемещения рабочего плеча на нужное расстояние, точку приложения действующей силы необходимо переместить на столько же больше (меньше), каково соотношение плеч, то есть пропорционально выигрышу в силе, который мы хотим получить. Другими словами, закон рычага, сформулированный ешё в античные времена, заключается в следующем: сколько выиграем в силе — проиграем в пути, и наоборот. Каждый раз, собираясь использовать рычаг, необходимо помнить об этом — ведь механическая работа (и необходимая для её совершения энергия) равна произведению приложенной к телу силы на пройденный им путь, т.е. рычаг принципиально не может дать выигрыш в энергии!
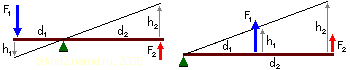 Один цвет (любой) соответствует приложенной к рычагу внешней силе, другой — силе, с которой рычаг будет действовать на размещённое в этом месте тело. d — плечи, F — силы, h — перемещения точек приложения сил.
На рисунке слева моменты приложены по разные стороны от оси, справа — с одной стороны, однако всегда d1/ d2 = h1/ h2 = F2/ F1 (если длину плеч считать от оси поворота, то плечи с разных сторон от оси будут также иметь разные знаки).
Закон рычага применим к любым механическим устройствам, изменяющим силу — не только к прямым «палочным» рычагам, но и к полиспастам (также известным с античных времён), а также к шестерёнчатым, цепным и ременным передачам. Более того, аналогичные закономерности действуют не только в механических устройствах. Например, в гидравлике плечам соответствуют площади поршней, а сила также обратно пропорциональна перемещению, поэтому совершаемая работа и передаваемая энергия не изменяются, не считая потерь на трение. И даже в электромагнетизме в обычном трансформаторе плечам аналогично число витков в обмотках, а изменение напряжения обратно пропорционально изменению тока, так что передаваемая мощность и энергия тоже не меняются за вычетом неизбежных потерь на нагрев.
Понятие об устойчивом и неустойчивом равновесии и потенциальном барьере
В потенциальном поле при отсутствии других внешних сил (включая силы трения) тело, опирающееся на опору, может быть в неуравновешенном состоянии, либо находиться в состоянии устойчивого или неустойчивого равновесия.
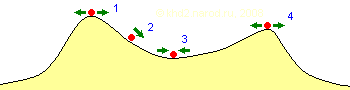 1 1 и 4 — неустойчивое равновесие, 2 — неуравновешенное состояние, 3 — устойчивое равновесие, стрелками показаны возможные направления движения тела после небольшого внешнего воздействия.
В состоянии неустойчивого равновесия теоретически тело может оставаться неподвижным сколь угодно долго, однако любое внешнее воздействие инициирует нарастающее движение тела, удаляющее его от первоначального положения даже после прекращения инициирующего воздействия. Для возврата в исходное положение телу требуется затратить кинетическую энергию. В положении неустойчивого равновесия потенциальная энергия тела максимальна (по крайней мере, в ближайших окрестностях этого положения). В примере рычага с грузом положению неустойчивого равновесия груза соответствует верхняя мёртвая точка (ВМТ).
В неуравновешенном состоянии изначально покоящееся тело, будучи отпущенным, немедленно начинает движение в сторону с меньшей потенциальной энергией, а если к этому моменту оно уже двигалось, то будет изменять свою исходную скорость, переводя потенциальную энергию в кинетическую. Для возврата в исходное положение телу требуется затратить кинетическую энергию. В примере рычага с грузом неуравновешенному состоянию груза соответствуют все положения между верхней и нижней мёртвыми точками.
В состоянии устойчивого равновесия тело может оставаться неподвижным сколь угодно долго, при этом внешнее воздействие может вывести тело из этого положения, придав ему дополнительную внешнюю энергию. Однако после того, как это воздействие снято, тело стремится вернуться в исходное положение, где потенциальная энергия тела минимальна. В ходе этого процесса избыточная потенциальная энергия, полученая в результате внешнего воздействия, превращается в кинетическую. В примере рычага с грузом положению устойчивого равновесия груза соответствует нижняя мёртвая точка (НМТ).
Если между двумя положениями устойчивого равновесия есть точка с положением неустойчивого равновесия, то для того, чтобы тело перешло из одного устойчивого положения в другое, ему надо сообщить столько энергии, чтобы сумма его текущей кинетической и потенциальной энергии превысила потенциальную энергию, характерную для преодолеваемого положения неустойчивого равновесия. Эта энергия называется потенциальным барьером. Область между двумя потенциальными барьерами называется потенциальной ямой. Так, на рисунке тела, изначально находящиеся в положениях 2 и 3 в покое (с нулевой кинетической энергией) не могут покинуть область потенциальной ямы без получения извне дополнительной энергии. Потенциальная энергия тела, находящегося в положении 1, больше уровня другого потенциального барьера (4), поэтому оно может двигаться без ограничений как влево, так и вправо. А вот потенциальной энергии тела в положении 4 недостаточно, чтобы преодолеть более высокий потенциальный барьер слева.
Чтобы тело прошло через потенциальный барьер, не обладая минимальной достаточной энергией, оно должно пройти сквозь опорную поверхность — в таком случае будет наблюдаться туннельный эффект. В макромире, описываемом классической механикой, достоверные случаи туннельного эффекта не известны.
Изменение давления с глубиной
В конструкциях с погружёнными в жидкость элементами изменяемого объёма обязательно необходимо учитывать разность давлений на различной глубине. Как же определить эту разность давлений? Давление жидкости с открытой поверхностью на некоторой глубине d при её удельной плотности ρ на поверхность тела площадью S в гравитационном поле с ускорением свободного падения g определяется весом столба жидкости, высота которого равна d, а площадь сечения — S:
P = (ρ · d · S · g) / S = ρ · d · g (3).
Сразу следует отметить два очень важных момента, которые иногда упускают из вида: во-первых, давление в жидкости всегда направлено перпендикулярно поверхности погружённого тела независимо от её ориентации в пространстве, и, во-вторых, это верно тогда, когда поверхность ориентирована строго горизонтально, либо силу давления можно рассматривать как приложенную к геометрическому центру этой поверхности, как раз и находящемуся на глубине d (обычно применимо в случае жёстких поверхностей), либо линейные размеры поверхности много меньше глубины, так что разность давления на верхнем и нижнем краю этой поверхности пренебрежимо мала по сравнению с его абсолютной величиной. Во всех остальных случаях необходимо рассматривать давление на каждый фрагмент поверхности по отдельности или выбирать наихудший случай.
А сила давления F на поверхность площадью S на глубине d равна
F = P · S = ρ · d · S · g (4).
Однако часто абсолютное давление не играет большой роли — его можно компенсировать, подкачав при монтаже и настройке внутрь конструкции воздух до примерно такого же давления. Но вот разность давлений при нахождении элемента конструкции в верхней и нижней точках (если, конечно, сама конструкция предусматривает перемещение в вертикальной плоскости) так компенсировать не удастся, и именно необходимость преодоления разности давлений на разных глубинах может «съесть» всю полезную работу. Как же определить разность давлений на разных глубинах? Для этого достаточно в формуле (3) вместо абсолютной глубины d подставить разность глубин. Соответственно, такая же замена в формуле (4) покажет силу, необходимую для преодоления разности давлений в верхнем и нижнем положениях. Ещё раз подчеркну, разность давлений актуальна только в том случае, если объём элемента (поплавка) изменяется. Для поплавков с постоянным объёмом достаточно учитывать только силу тяжести (вес) и силу плавучести (Архимеда).
Всё вышесказанное верно не только для жидкостей, но и для газов, однако из-за малой удельной плотности газа при обычных условиях на небольшой разности высот (в несколько метров) его давление различается настолько мало, что в подавляющем большинстве случаев этой разницей можно пренебречь и считать давление одинаковым.
Эффект Архимеда и его особенности
Приходя к осознанию бесперспективности попыток заставить одну и ту же силу работать против себя самой и получать при этом дополнительную энергию, всё больше изобретателей стараются использовать пару альтернативных сил и попытаться получить их дисбаланс с выходом полезной энергии. В механических устройствах очень часто в качестве альтернативы силе тяжести, а иногда и инерционным силам используется сила Архимеда. В связи с этим я считаю необходимым подробно рассмотреть этот эффект (собственно физическим явлением является именно эффект, а сила возникает или не возникает как результат этого эффекта) и предотвратить иллюзии, ведущие к заведомо бесперспективным затратам сил, средств и времени.
Как известно, эффект Архимеда заключается в том, что при разности давлений на противоположные грани тела, находящегося в подвижной среде (жидкой или газообразной), возникает воздействующая на это тело сила, направленная в сторону меньшего давления. При этом именно об эффекте Архимеда речь идёт в том случае, если разность давлений вызывается объёмными силами, то есть силами, воздействующими не на поверхности, а на весь объём (массу) среды погружения — обычно имеется в виду гравитационное поле, однако это может быть и магнитное поле (для магнитных жидкостей), электростатическое поле (для жидкостей с заряженными частицами), а также инерционные силы, в том числе и центробежные. Большинство таких сил в традиционной физике называются «полевыми», так как вызываются гравитационным, магнитным или электростатическим полями, но силы инерции к полевым обычно не относят, поэтому я использую термин «объёмные силы». В отсутствие таких сил отсутствует и эффект Архимеда, даже если среда (газ или жидкость) находится под давлением. Широко известны опыты в невесомости, когда жидкость либо прилипает к стенкам сосуда, либо собирается в его центре в зависимости от смачиваемости или несмачиваемости внутренней поверхности, а другие тела, находящиеся в том же сосуде, могут либо вовлекаться ею в себя, либо отторгаться по тем же причинам. Однако в таких условиях жидкость не стремится собраться в какой-либо одной части сосуда, а взаимодействие её с другими телами практически не зависит от их плотности, в отличии от того, что происходит под воздействием силы тяжести или при воздействии на сосуд в невесомости инерционных сил в момент его разгона или торможения.
Поэтому можно сказать, что по своей сути сила Архимеда является своеобразным отражением объёмных сил, действующих на среду, в которой находится тело. При этом она всегда направлена строго противоположно направлению силы, создающей разность давлений. В случае воздействия нескольких таких сил одновременно (например, магнитная жидкость во вращающемся сосуде, находящемся в гравитационном и магнитном полях), результирующая сила Архимеда является векторной суммой всех «элементарных» сил Архимеда, вызванных каждой из воздействующих на среду сил в отдельности.
Таким образом, эффект Архимеда можно рассматривать как своего рода «зеркало» объёмных сил, действующих на тела в подвижных средах. И также, как оптическое зеркало может перенаправить свет туда, куда он не попадает напрямую от источника, и даже сконцентрировать его, но не может дать света больше, чем его поступило от этого источника, так и эффект Архимеда может изменить направление действия объёмной силы, но не может дать её прибавки, а следовательно, дополнительной работы и энергии.
Справедливость законов классической механики
Следует подчеркнуть, что за несколько веков, прошедших с момента формулирования основных законов механики (а интуитивно их используют уже многие тысячи лет), не возникло веских причин, вынуждающих усомниться в их справедливости и, стало быть, не было причин скорректировать эти законы. Единственный общепризнанный случай, когда в них были внесены поправки и дополнения — это разработка релятивистской теории, однако и там поправки сформулированы таким образом, что их влияние заметно лишь в экстремальных условиях космических скоростей и масс, а «в комнате» их вклад стремится к нулю и намного меньше точности обычных средств измерения. В случае же тихоходных механических устройств никаких экстремальных условий и близко не видно!
♦
|