Системы колёс с эксцентриками

Системы колёс с эксцентричным расположением грузов представляют собой весьма своеобразный класс механических «вечных двигателей». Они состоят из нескольких колёс, синхронизированно вращающихся вокруг общего центра таким образом, что плечо груза на стороне рабочего хода больше плеча во время обратного хода. Это должно создавать разность вращающих моментов, обеспечивающих «вечную» работу такой установки. В этом их отличие от конструкций с дисбалансом, где вращение должна обеспечить не разность плеч, а разность веса грузов на рабочей и обратной сторонах. Поэтому конструкции с дисбалансом обычно реализуются в «цепных» вариантах, а вот конструкции с эксцентриками должны оставаться «колёсными». Зато установки с эксцентриками очень похожи на узлы конструкций с дебалансом, например те, которые разрабатывает Э.И.Линевич. Отличие здесь заключается в назначении эксцентриков: в нашем случае они должны непосредственно обеспечить рабочий вращающий момент без дополнительного двигателя, а у того же Линевича нужны лишь для того, чтобы вызвать необходимые колебания и приводятся во вращение специальным двигателем. Поэтому кинематика установок в целом, конечно, различается.

Планетарная конструкция с «обгоняющими» эксцентриками
   Варианты конструкции
   Расчёт конструкции
      Расчёт положения эксцентрика в системе отсчёта вращающейся рамы
      Расчёт положения эксцентрика относительно вертикали
      Результаты расчёта
   Планетарная обгонная муфта с эксцентриками
Конструкция с «фиксированным» положением эксцентрика

Планетарная конструкция с «обгоняющими» эксцентриками

Эта конструкция подобна планетарным редукторам — вокруг центрального колеса вращается рама с несколькими (от 1 до 5) свободно вращающимися колёсами-сателлитами того же диаметра, которые снабжены тяжелыми эксцентриками и катятся по центральному колесу без проскальзывания. Однако в отличии от большинства планетарных редукторов центральное колесо здесь неподвижно, а внешняя обечайка (корпус) отсутствует — её заменяет рама.

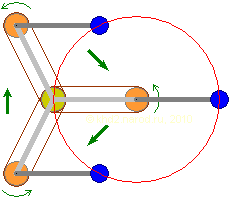
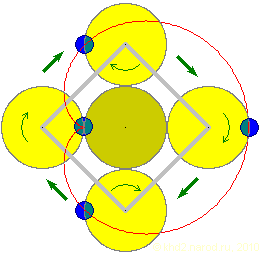Планетарная конструкция с «обгоняющим» эксцентриком. Левая сторона — обратный ход, правая — рабочий.
Тёмно-жёлтым показано центральное неподвижное колесо, светло-жёлтым — вращающиеся колёса-сателлиты, синим — грузы-эксцентрики, закреплённые на сателлитах, светло-серым — рама, соединяющая оси сателлитов. Зелёными стрелками указаны направления вращения рамы и сателлитов. Красным цветом показана траектория движения центра масс эксцентрика.

Поскольку при окатывании сателлитом центрального неподвижного колеса движение рамы и жёстко закреплённой в ней оси сателлита складывается с собственным вращением сателлита, с точки зрения внешнего наблюдателя за один оборот рамы сателлит с эксцентриком совершит два оборота, как бы обгоняя вращение рамы, хотя в системе отсчёта, связанной с рамой, будет только один оборот, и, независимо от системы отсчёта, только один раз за оборот рамы эксцентрик пройдёт через точки с минимальным и максимальным плечом. Поэтому я называю эту конструкцию «планетарной с обгоняющим эксцентриком».

Очевидная на рисунке немалая разность плеч на левой и правой сторонах устройства обещает большую разность вращающих моментов, и это привлекает изобретателей. Прежде, чем проверить работоспособность расчётом, обсудим возможные варианты конструкции.

Варианты конструкции

Рассмотрим чуть подробнее технические аспекты. Для предотвращения проскальзывания сателлитов по центральному неподвижному колесу поверхности всех колёс можно сделать рифлёными, а лучше всего использовать шестерни подходящего диаметра с некрупным зубом. На верхнем рисунке грузы-эксцентрики закреплены на сателлитах таким образом, что их центры масс совпадают с краем сателлитов, — это удобно для расчёта, а технически реализуется с помощью кронштейнов или выносов. Однако можно отступить чуть вглубь колеса, так, чтобы габариты эксцентрика не выходили за габариты сателлита, тогда эффективность немного уменьшится, но принципиально ничего не изменится. Именно так реализована схема А.В.Малышева из Санкт-Петербурга (публикуется с разрешения автора, именно он побудил меня подробно рассмотреть этот класс устройств).

При трёх и более сателлитах рама может вообще не иметь центральной оси — сателлиты обеспечат её удержание на неподвижном центральном колесе и соосность её вращения с центральной осью всей конструкции, совпадающей с центром неподвижного колеса. Именно такой вариант и показан на рисунке вверху. Однако, поскольку мощность удобнее всего снимать именно с вращающейся рамы, скрепляющей оси сателлитов, может понадобится жёстко связанная с ней центральная ось.

Какие ещё возможны варианты? Посмотрим, что получится при попытке сделать диаметры центрального колеса и сателлитов различными. Если диаметр сателлитов будет меньше диаметра неподвижного колеса в целое число раз, скажем, в 2 или в 3 раза, то траектория эксцентриков станет симметричной, и суммарный вращающий момент будет равен нулю — аналогично симметричному размещению нескольких грузов на ободе колеса.

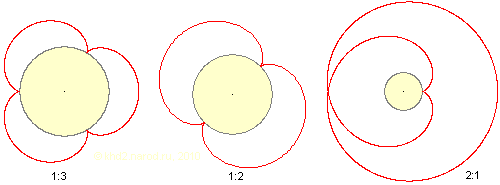Траектории эксцентриков при разных соотношениях диаметров центрального колеса и сателлитов. Помимо траектории (красным) показано центральное неподвижное колесо (серым).

Если же центральное колесо будет меньше сателлитов в целое число раз, то полную траекторию эксцентрик будет проходить не за один оборот рамы, а за такое их количество, которое численно равно соотношению диаметров колёс. При этом на рисунке видно, что моменты с бóльшим плечом на одном обороте будут «съедены» моментами с меньшим плечом на следующих оборотах, так что в результате выигрыша ждать не приходится.

Наконец, в случае некратного соотношения диаметров точки наиболее и наименее выгодных моментов будут перемещаться по кругу, и на длительном интервале времени полностью компенсируют друг друга. Отсюда вывод — выигрыша можно ожидать, только если диаметры центрального колеса и сателлитов в точности равны! Только тогда траектория эксцентриков имеет один максимум и один противоположный ему минимум, а положение этих точек остаётся неизменным при любом количестве оборотов.

Какие ещё вариации возможны? Можно изменять число сателлитов — от 1 (в этом случае для обеспечения стабильного вращения понадобится тяжёлый маховик) до 5. Теоретически в одной плоскости вокруг центрального колеса можно разместить 6 сателлитов того же диаметра, однако на практике (особенно в случае использования шестерней) они войдут в зацепление не только с центральным колесом, но и друг с другом — таковы законы геометрии. При этом в месте контакта края соседних сателлитов должны двигаться встречно — в результате конструкция не сможет двигаться вообще! Впрочем, для повышения мощности нам никто не мешает объединить в одной раме несколько групп сателлитов, вращающихся вокруг одной длинной оси, либо (что проще) увеличить размеры колёс и вес эксцентриков.

Наконец, можно заменить раму внешним корпусом-обечайкой, как это сделано в планетарных редукторах. В этом случае вообще отпадает необходимость в осях и подшипниках! Однако в отличии от редукторов у нас центральное колесо будет неподвижно, а вращаться будет внешний корпус, с которого и можно будет снимать мощность.

И всё же, всё это будет иметь смысл только в том случае, если базовый вариант конструкции покажет положительный выход работы! Пора переходить к расчётам.

Расчёт конструкции

Для определения работоспособности конструкции используем стандартный критерий — необходимость положительной суммарной работы за полный цикл движения одного элемента. В нашем случае этот критерий эквивалентен критерию положительного суммарного вращающего момента от сателлита с эксцентриком за полный цикл.

В качестве угла поворота следует выбрать угол поворота рамы с осями сателлитов, поскольку именно отсюда отбирается нагрузка, а её вращение достаточно равномерно, особенно при наличии большого количества эксцентриков. За исходное положение примем положение оси сателлита вертикально вверх над центром неподвижного колеса, как и при рассмотрении других конструкций в данном разделе (хотя здесь несколько более логично было бы выбрать, скажем, положение слева от центра — там особая точка траектории эксцентрика, но по большому счёту для замкнутой траектории это не имеет принципиального значения). Траектория движения эксцентрика выглядит весьма сложной, однако не всё так печально, если сначала посчитать поворот эксцентрика относительно рамы, а затем учесть и поворот самой рамы с осью сателлита вокруг центра всей конструкции, совпадающего с центром неподвижного колеса.

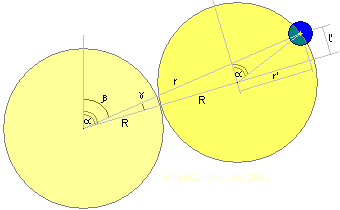Схема расчёта положения эксцентрика во время работы.

Итак, ещё раз посмотрим на исходные данные. Выше мы уже установили, что радиусы центрального колеса и сателлита должны быть строго равны. Обозначим их символом  R. При выбранном исходном положении (ось сателлита строго над центром конструкции) исходное положение эксцентрика будет строго слева от оси сателлита (соответствует верхнему сателлиту на самом первом рисунке на этой странице). И рама вокруг общего центра, и сателлит вокруг своей оси вращаются по часовой стрелке. Поскольку радиусы колёс равны, то насколько рама повернётся от своего исходного положения в неподвижной внешней системе отсчёта, настолько же эксцентрик повернётся от своего исходного положения в системе отсчёта, связанной с вращающейся рамой. Обозначим эти углы символом  α. Для расчёта текущего вращающего момента нам надо найти расстояние от оси вращения всей конструкции до текущего положения центра масс эксцентрика (r) и угол отклонения от вертикали линии, соединяющей центр неподвижного колеса и текущее положение центра масс эксцентрика (β), либо угол его опережения-запаздывания относительно поворота рамы (γ), которые взаимосвязаны по формуле

Расчёт положения эксцентрика в системе отсчёта вращающейся рамы

В соответствии с вышеизложенным планом сначала рассчитаем положение эксцентрика относительно нормали, проходящей через ось сателлита к общему центру вращения конструкции. Поскольку эксцентрик как бы «запаздывает» на 90°, его проекции следует вычислять как

Расчёт положения эксцентрика относительно вертикали

Теперь надо определить положение эксцентрика относительно центра вращения рамы. Очевидно, что проекция его положения на нормаль от оси сателлита к центру вращения рамы  r" будет больше  r' на сумму радиусов обоих колёс:

Зная это и его тангенциальную проекцию  l', легко вычислить угол отставания или опережения эксцентрика относительно нормали от оси сателлита

Расстояние от общего центра вращения до центра масс эксцентрика вычисляется из  r" и  l' по теореме Пифагора

Теперь не составляет труда по формуле (1) определить угол отклонения центра масс эксцентрика от вертикали  β и вычислить вращающий момент, равный весу эксцентрика, умноженному на  r и на  sin(β). Положительные значения будут соответствовать вращающему моменту, разгоняющему раму в выбранном нами направлении, а отрицательные — тормозящему.

Результаты расчёта

Подробные результаты расчёта по формулам (2)—(5) приведены в таблице на отдельной странице. Здесь же я сразу скажу: общий результат — нулевой. Почему так произошло, ведь несимметричность траектории очевидна?

Ответ можно найти в той же таблице. Кинематика движения эксцентриков такова, что в «отрицательной» тормозящей области они движутся медленнее, чем в «положительной» разгоняющей. Например, при вертикальном положении оси сателлита эксцентрик отклоняется в «отрицательную» область на 26.6°, а в «положительную» переходит только тогда, когда угол поворота рамы превысит 21.4°. Таким образом, при своём вращении рама разгоняется на протяжении чуть менее 137°, а тормозится чуть более чем 223°. Это более длительное, хотя и более слабое, торможение полностью компенсирует более интенсивный, но более короткий разгон. Соотношение секторов положительной и отрицательной работы эксцентрика для угла поворота рамы наглядно показано на рисунке справа (зелёный сектор — разгон, красный — торможение).

Планетарная обгонная муфта с эксцентриками

Хотя «вечный двигатель» у нас опять не получился, эта конструкция может найти одно довольно неожиданное практическое применение — в качестве обгонной муфты, позволяющей преобразовывать вращательные колебания центрального колеса в однонаправленное вращение рамы или внешней обечайки.

Традиционные конструкции обгонных муфт при переключении направления вращения приводного вала имеют довольно большой люфт — от нескольких угловых градусов до десятка градусов и больше. В результате для эффективного преобразования вращательных колебаний центрального колеса во вращательное движение, угол этих колебаний должен составлять десятки градусов. Примеры таких устройств — храповое колесо с «собачками» (в заднем колесе почти всех велосипедов с переключением передач) или обойма со специальными втулками внутри, прижимающими ролики к внутренней поверхности задней втулки в велосипедах с «ножным» тормозом (классический дорожный велосипед, где для торможения надо повернуть педали назад).

В нашем же случае люфт определяется зазором между зубьями центрального колеса и сателлитов и может составлять лишь малые доли градуса, поэтому даже колебания центрального колеса на считанные градусы могут быть эффективно преобразованы во вращательное движение! Правда, и здесь не обошлось без ложки дёгтя. Всё это возможно лишь тогда, когда сумма тормозящего момента от нагрузки и собственного момента инерции рамы или обечайки относительно центра их вращения намного меньше суммы моментов инерции сателлитов относительно их осей. Зато здесь нет условия обязательного равенства диаметров центрального колеса и сателлитов...

Конструкция с «фиксированным» положением эксцентрика

Если в предыдущей конструкции с точки зрения внешнего наблюдателя эксцентрик как бы «обгонял» вращение рамы, то теперь попробуем сделать так, чтобы он, наоборот, с точки зрения того же наблюдателя имел один и тот же угол наклона. Для этого надо заставить сателлиты вращаться в сторону, противоположную вращению рамы, сохранив угловые скорости вращения одинаковыми.

Добиться этого просто. Достаточно зафиксировать на центральном неподвижном валу зубчатые звёздочки и соединить их цепью с такими же звёздочками, жёстко прикреплёнными к сателлитам. Можно добиться того же эффекта и с помощью системы шестерён, как это показано в одном из роликов на YouTube. Кинематика движения грузов в обоих случаях одинакова, но в дальнейшем я буду рассматривать вариант с цепью — в нём меньше деталей и нагляднее их взаимосвязь.

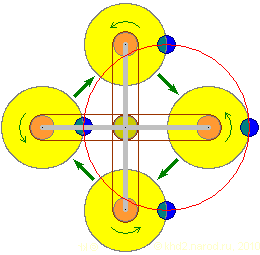Конструкция с «неподвижным» эксцентриком. Левая сторона — обратный ход, правая — рабочий.
Тёмно-жёлтым показана центральная неподвижная звёздочка, светло-жёлтым — вращающиеся колёса-сателлиты, оранжевым — звёздочки сателлитов, коричневым — цепи, синим — грузы-эксцентрики, закреплённые на сателлитах, светло-серым — рама, соединяющая сателлиты. Зелёным стрелками указаны направления вращения рамы и сателлитов. Красным цветом показана траектория движения центра масс эксцентрика.

Для эксцентрика следует выбрать наиболее оптимальное положение — максимально удалить его от оси сателлита в сторону, куда предполагается вращение конструкции. В нашем случае это будет вправо от оси. В отличии от предыдущего варианта, теперь эксцентрики движутся по своей траектории равномерно, а сама траектория представляет собой ту же окружность, по которой вращаются оси сателлитов, только смещённую от центра вращения рамы в нужную нам сторону на расстояние между осью сателлита и центром масс эксцентрика. Теперь-то уж мы наверняка получим суммарный положительный момент! И действительно, для показанного на рисунке случая, когда расстояние между осью сателлита и центром масс эксцентрика вдвое меньше радиуса вращения самой оси сателлита вокруг центрального вала, расчёт для движения по замкнутому контуру дал полезную суммарную работу, равную 33.333% от той, которую эксцентрик обеспечит, просто опустившись из верхнего положения!

И это ещё не всё! Во-первых, сами сателлиты здесь не нужны — достаточно лишь звёздочек и рычагов, соединяющих эти звёздочки с грузами (которые уже нельзя назвать эксцентриками). А это значит, что в одной плоскости можно разместить не 5 и не 6 элементов, а гораздо больше — ведь все рычаги всегда имеют горизонтальное положение и не мешают друг другу. Более того, технически возможно удлинить рычаги даже больше, чем длина рамы между центральным валом и осью рычага (бывшей осью сателлита). Тем самым вся траектория груза выносится в «положительную» область, и работа может достигать работы, соответствующей простому опусканию груза на высоту всей конструкции, а при дальнейшем удлинении рычагов (технически ограниченном лишь пределом прочности материалов) — и во много-много раз превышать её!

Усовершенствованная конструкция с удлинёнными рычагами, всегда обеспечивающая неотрицательный вращающий момент от груза (вариант с тремя грузами).
Тёмно-жёлтым показана центральная неподвижная звёздочка, тёмно-серым — рычаги с грузами, синим — грузы-эксцентрики, оранжевым — звёздочки рычагов, коричневым — цепи, светло-серым — рама, соединяющая сателлиты, зелёным — направления вращения рамы и звёздочек рычагов. Красным цветом показана траектория движения центров масс грузов.

Так что же, мы получили вечный двигатель почти неограниченной мощности, который может сделать любой, кто в состоянии разобрать и собрать велосипед? Увы, нет! Тех, кто попробует реализовать всё это в натуре, ждёт жестокое разочарование — ничего похожего на вечное вращение не будет! Почему?

Расчёт моментов выполнен верно, но здесь действует ещё один фактор, которого не было в предыдущей планетарной конструкции. Там колёса с грузами-эксцентриками вращались свободно, а здесь рычаги с грузами принудительно удерживаются цепью в наиболее выгодном положении — строго вправо от оси вращения рычага. При этом вращающий момент, стремящийся повернуть рычаг с грузом на его оси, компенсируется натяжением цепи, удерживающей его в этом положении.

Очевидно, что как только порвётся цепь, груз повиснет вертикально вниз, и его траектория будет смещена уже не в сторону, а по вертикали, и потому никакой разности моментов относительно центральной оси вращения не будет. Таким образом, весь нескомпенсированный вращающий момент, который должен ускорять вращение рамы, обусловлен именно смещением груза в сторону от вертикали. Но ведь именно этот момент и компенсируется натяжением цепи, а натянутая таким образом цепь вращение рамы стремится остановить!

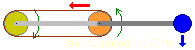Натяжение цепи — причина торможения вращения.
Синяя стрелка показывает вес груза, красная — компенсирующую реакцию цепи.

На рисунке хорошо видно, что момент, создаваемый реакцией цепи (красная стрелка), противоположен тому, что создаёт вес груза (синяя стрелка). При этом действует закон рычага — усилие цепи больше веса груза во столько же раз, во сколько радиус звёздочки меньше длины соединённого с ней рычага, на котором закреплён груз. Поскольку это соотношение и угол наклона рычага с грузом относительно вертикали во время работы не изменяется, это усилие постоянно. Вращающий же момент от веса груза, разгоняющий конструкцию, меняется в зависимости от угла поворота рамы, но в сумме он оказывается равен суммарному тормозящему моменту, вызванному воздействием цепи, обеспечивающей нужное положение рычага с грузом. ♦