Гравитационные весы

Не так давно Сергей Портнов прислал мне схему одной чисто механической конструкции, гениально простую и на первый взгляд абсолютно работоспособную. Поскольку её основная кинематика практически копирует механизм рычажных чашечных весов, в советское время широко использовавшихся на колхозных рынках, я назвал её «гравитационными весами». Однако из многих миллионов пользователей колхозных весов ни один так и не нашёл секрета вечного движения, хотя некоторые из них в ожидании покупателей наверняка катали по чашкам картофелины или положенные на бок круглые гирьки. В чём же дело?

Конструкция гравитационных весов
Модификация гравитационных весов
Анализ гравитационных весов
Попытка доработки гравитационных весов

Конструкция гравитационных весов

Рисунок наглядно демонстрирует внешний вид гравитационных весов, по которому можно легко понять принцип их работы. Ниже приведена их кинематическая схема.

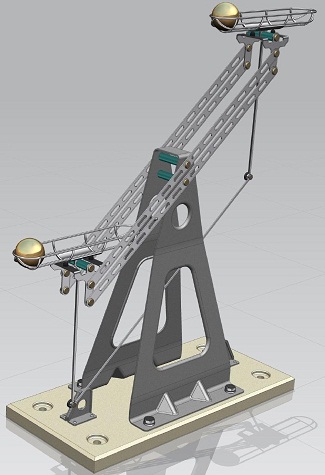Компьютерная визуализация модели гравитационных весов (С.Н.Портнов).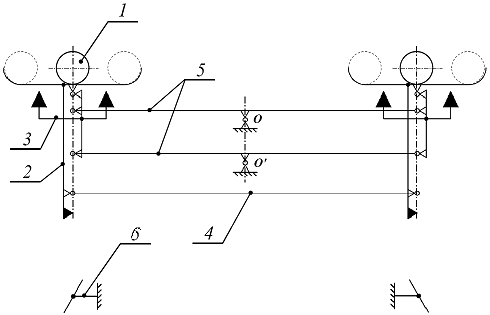

Кинематическая схема гравитационных весов (С.Н.Портнов). Цифрами обозначены: 1 — груз; 2 — направляющая («чашка» со штоком); 3 — опора направляющей; 4 — тяга; 5 — рычаги; 6 — упор, изменяющий наклон направляющих.

Предполагается, что направляющие (аналоги чашек рыночных весов) независимо от наклона рычагов всегда находятся в положении, близком к горизонтальному, что обеспечивается параллелограммом, состоящим из пары рычагов и пары опор направляющих. Однако наклон направлящих может немного изменяться, обеспечивая синхронное перемещение одинаковых шаров-грузов на тот или другой край направляющих. Для этого служат жёстко связанные с направляющими штоки и упоры под ними, отклоняющие шток в нужную сторону при достижении нижнего положения. Тяга обеспечивает синхронное изменение наклона противоположной направляющей.

Предполагается, что смещение груза относительно центра направляющей создаёт разность моментов силы относительно оси рычага, что и должно обеспечить поворот рычагов. При достижении крайнего положения шток через упор и тягу изменяет наклон чашек-направлющих на противоположный, и шары перекатываются на другой их край. В результате суммарный момент сил на рычагах меняется на противоположный, и весы совершают обратный ход. Затем всё повторяется.

Особо следует отметить, что для перекатывания шаров в противоположное положение достаточно очень малого изменения наклона направляющих, настолько малого, что работой по подъёму шара, неизбежной в такой ситуации, можно просто пренебречь по сравнению с работой, которая получается при изменении положения весов. Кажется, что всё учтено и никаких «подводных камней» здесь нет, а стало быть гравитационные весы просто обязаны работать.

Однако перед дальнейшим анализом попробуем модифицировать конструкцию, ещё более упростив и без того несложную кинематику.

Модификация гравитационных весов

Для упрощения кинематики мы откажемся от изменения наклона чашек-направляющих, сделав их постоянно строго горизонтальными. В самом деле, их наклон изменяется только для перемещения шара в противоположный конец, но это можно обеспечить и другими средствами, напрмер с помощью неподвижных выступов-толкателей, размещённых в крайних положениях хода весов и обеспечивающих шару перемещающий импульс при опускании или поднимании сответствующей чашки за счёт вертикального импульса самого шара, приобретённого им в ходе изменения наклона весов. Перекатывающий импульс может быть весьма небольшим и гораздо меньше, чем вертикальный импульс шара в конце рабочего хода. Для фиксации шара в противоположном положении в конце направляющей можно предусмотреть мягкий демпфер, гасящий перекатывающий импульс шара, и фиксатор (маленький порожек или слабый магнит), удерживающий шар в крайнем положении.

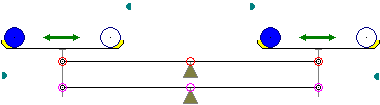Модифицированные гравитационные весы. Голубым показаны неподвижные толкатели, жёлтым — демпферы-фиксаторы шаров. Красным и сиреневым выделены оси поворота и точки приложения сил (плечи) верхнего и нижнего рычагов соответственно.

Теперь кинематика весов минимизирована, и можно приступить к её анализу. Отмечу, что кинематика этого варианта абсолютна идентична классической кинематике рычажных чашечных весов — лишь размещение грузов в чашках весов обычно не показывается...

Анализ гравитационных весов

В модифицированной схеме очевидно, что наклон меняют лишь два параллельных рычага, а значит, надо анализировать воздействия именно на них. Для того, чтобы качался рычаг, необходима разность моментов сил на его плечах, а при равенстве плеч — разность самих сил. Между тем в нашем случае точками приложения сил, непосредственно воздействующих на рычаг, являются шарниры крепления чашек с грузом, поэтому плечи равны, а силы определяются весом грузов, которые одинаковы в обоих чашках-направляющих. В результате сила, действующая на рычаг относительно его точки поворота, будет равна нулю независимо от положения груза в чашках весов (на рисунке концы плеч и точка поворота верхнего рычага обозначены красным, нижнего — сиреневым).

А что же тогда меняется при изменении положения груза в чашке? Меняется опрокидывающий момент самой чашки, но он всегда компенсируется жёсткостью параллелограмма весов.

Должен сказать, что с самого начала для меня всё это отнюдь не было очевидным. В данном случае ложные надежды даёт неверная интерпретация кинематики. Если в большинстве случаев, рассмотренных в данном разделе сайта, грузы воздействуют непосредственно на колесо или рычаг, то здесь их действие происходит опосредовано через параллелограмм из двух рычагов и двух штоков. Однако постоянную вертикальность штока, на котором закреплена чашка весов, можно обеспечить и другими способами, например с помощью направляющей втулки. И тогда отсутствие каких-либо предпосылок к вечному движению становится намного нагляднее, с чем согласился и Сергей Портнов, безоговорочно признав неработоспособность конструкции.

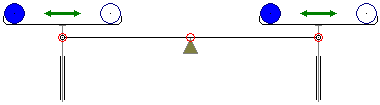Схема гравитационных весов, в которых горизонтальность чашек обеспечивают направляющие втулки. Красным выделены ось поворота и точки приложения сил (плечи) рычага.

Попытка доработки гравитационных весов

Однако не менее очевиден тот факт, что если не пытаться удерживать горизонтальность направляющих, а позволить им наклоняться вместе с рычагом, то разность моментов сыграет свою роль, и рычаг повернётся. Попробуем сыграть на этом, и зафиксировав чашки относительно рычага во время рабочего хода, постараемся изменить их наклон в его крайних точках за счёт энергии, накопленной во время движения рычага.

Вроде бы всё получается, но... при изменении наклона направляющих в конце рабочего хода в силу геометрических законов один из грузов неизбежно придётся приподнимать, причём высота этого подъёма прямо пропорциональна высоте рабочего хода и создаваемой при этом разности моментов. Как вариант, можно приподнять оба груза на вдвое меньшую высоту. При этом для малых углов наклона рычага, когда cos(α) близок к 1, полезная работа будет равна

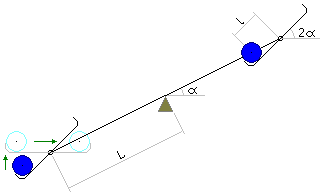Доработка гравитационных весов с поворотом направляющих в конце рабочего хода. Для упрощения кинематики ось поворота направляющих совпадает с концом рычага.

«Вредная» работа, необходимая для поднятия каждого груза, в этом случае будет равна

Поскольку при малых углах синус практически пропорционален самому углу, то можно вынести двойку из-под синуса, и мы увидим, что для двух грузов эта работа в точности равна полезной, то есть выигрыша нет. Для больших углов отклонения расчёт усложняется — там уже sin(2 · α) заметно меньше, чем 2 · sin(α) («вредная» работа уменьшается), но и cos(α) уже заметно меньше единицы, а стало быть, его уже нельзя не учитывать в расчёте. Из-за этого уменьшается разность плеч грузов, поскольку точное значение смещения груза от середины направляющей с учётом её наклона относительно рычага равно l · cos(α), так что разность моментов сил уменьшается, и обусловленная ею полезная работа тоже становится меньше. Поэтому общий результат остаётся по-прежнему нулевым. ♦