Водяное колесо с фиксированным краном
Необычная конструкция водонаполненного колеса-«мельницы».
Исходный вариант
Конструкция исходного варианта
Расчёт исходного варианта
Модифицированный вариант
Конструкция модифицированного варианта
Расчёт модифицированного варианта
Исходный вариант
Конструкция исходного варианта
Здесь используется перемещение жидкости между резервуарами в 2 этапа одинаковыми порциями: сначала 25% и затем ещё 25%, при этом каждый раз жидкость перемещается не на диаметр колеса, а всего лишь на его радиус. Особого внимания заслуживает оригинальная система коммутации резервуаров. Она представляет собой неподвижную центральную часть крана с просверленными в ней под необходимым углом каналами, вокруг которой вращается подвижный корпус с жёстко прикреплённой к нему крестовиной с резервуарами. Вес грузов на поршнях (или мембранах) обеспечивает необходимое перемещение жидкости между резервуарами, в результате чего должна получиться разность моментов, которая и приведёт колесо в движение. Конструкция предусматривает строго определённое число элементов, кратное четырём, причём каждая четвёрка является обособленной и должна коммутироваться независимо от других.
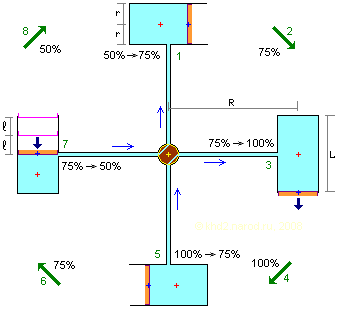
Водяное колесо с фиксированным краном. R — расстояние от оси вращения до центра масс жидкости и груза, r — радиус резервуара, L — полная длина резервуара, l — перемещение поршня с грузом при удалении / добавлении одной порции жидкости (на рисунке — 25%). Коричневым обозначена неподвижная сердцевина крана с просверленными в ней каналами, вокруг которой вращается внешний тонкий жёлтый корпус с жёстко прикреплённой к нему крестовиной с резервуарами. Жёлтый крестик обозначает ось вращения конструкции, красные крестики — положение центров масс жидкости, синие — центров масс поршней (фиолетовые) вместе с грузами (оранжевые). Зелёные цифры указывают номер фазы на соответствующем сегменте траектории элемента, а чёрные цифры — процент заполнения резервуара на этой фазе.
Явно заметен существенный дисбаланс между правой (рабочей) и левой (обратной) половинами траектории элементов. Посмотрим, хватит ли его для того, чтобы заставить колесо вращаться? Как всегда, для этого необходимо соблюдение основного условия успешной работы механических колёс.
Расчёт исходного варианта
За полный рабочий цикл каждый элемент проходит 8 фаз (с учётом вязкости жидкости на переключение элементов отводится по 5° перемещения точки отсчёта, в качестве которой выбираем место крепления резервуара к рычагу крестовины).
| Фаза |
Углы точки отсчёта для фазы |
Действия во время фазы |
| 1 |
356°..0° |
элемент соединён со следующим, откуда получает порцию жидкости (объём жидкости увеличивается с 50% до 75%) |
| 2 |
1°..85° |
элемент отключён от остальных, объём жидкости равен 75% |
| 3 |
86°..90° |
элемент соединён с предыдущим и откачивает оттуда порцию жидкости (объём жидкости увеличивается с 75% до 100%) |
| 4 |
91°..175° |
элемент отключён от остальных, объём жидкости равен 100% |
| 5 |
176°..180° |
элемент соединён со следующим, туда передаётся порция жидкости (объём жидкости уменьшается со 100% до 75%) |
| 6 |
181°..265° |
элемент отключён от остальных, объём жидкости равен 75% |
| 7 |
266°..270° |
элемент соединён с предыдущим и выкачивает туда порцию жидкости (объём жидкости уменьшается с 75% до 50%) |
| 8 |
271°..355° |
элемент отключён от остальных, объём жидкости равен 50% |
Трение, сопротивление среды и прочее в первом приближении можно не учитывать. Массы грузов на поршнях не изменяются. В качестве базового радиуса R выберем расстояние от оси колеса до центра масс жидкости при 100% заполнении резервуара элемента, а в качестве базового веса — вес жидкости в полностью заполненном резервуаре. Конструкция с поршнями обеспечивает только тангенциальное перемещение центров масс жидкости и грузов относительно точки отсчёта. Соотношение масс груза и порции жидкости строго определено: перемещение груза на расстояние l должно поднять порцию жидкости (исходное значение — 25% от полного объёма) на высоту R. Таким образом, мы имеем дело с гидравлическим рычагом, и масса груза должна быть равна
M = m · δ · R / l = m · δ · R / (δ · L) = m / k (1),
где m — масса жидкости в резервуаре при его заполнении на 100%, δ = l / L — доля объёма резервуара, равная перемещаемой порции, от 0 до 1 (0...100%, изначально 0.25, т.е. 25%), L — полная длина резервуара, k = L / R = (l / δ) / R — т.е. соотношение полной длины резервуара к расстоянию от центра масс жидкости в нём до оси вращения колеса. При этом следует отметить, что полученное соотношение не зависит от объёма перемещаемой порции жидкости — будь то весь объём резервуара или доли процента от него. В этом нет ничего удивительного, ведь здесь необходимо преодолеть давление, а оно зависит лишь от разности уровней, а не от объёма жидкости!
Однако при внимательном рассмотрении не всё так просто. Для перемещения жидкости вес груза должен преодолеть максимальную разность давлений, которая на рабочем ходе (фаза 3) изменяется от R + r - L / 2 + l до R + r - L / 2, а на обратном ходе (фаза 7) от R + r - L / 2 + l до R + r - L / 2 + 2 · l. Наихудшим вариантом с наибольшей разностью уровней является последний, для него и выполним расчёт. Вес груза должен компенсировать давление столба жидкости, действующего на поршень. Считая, что резервуар имеет цилиндрическую форму, получаем массу груза равной
M = (R + r - L / 2 + 2 · l) · g · ρ · π · r2 / g = (r + R - R · k / 2 + 2 · R · k · δ) · ρ · π · r2 (2),
где ρ — удельная плотность жидкости, а r — радиус резервуара.
Учитывая, что масса жидкости полностью заполненного резервуара равна m = ρ · π · r2 · L, получаем связь между массой груза и максимальной массой жидкости в резервуаре:
M = m · (r + R - R · k / 2 + 2 · R · k · δ) / L = (1 + k · (2 · δ - 0.5) + r / R) · m / k (3).
Внимательный анализ формулы (3) показывает, что если расстояние от оси вращения до центра резервуара будет намного больше размеров этого резервуара, то k = L/R и r/R будут стремиться к 0, и в таком случае формула (3) превратится в формулу (1).
Предположим поршень достаточно тонким, а груз равномерно размещённым по всей его площади. Предположим также, что при 100% заполнении резервуара центр масс жидкости в нём находится точно по нормали относительно оси вращения колеса. Тогда при заполнении резервуара на 50% в этом месте будет находиться поршень, переместившийся на расстояние 2 · l. Таким образом, геометрический расчёт сводится к решению прямоугольных треугольников. При этом в зависимости от наполнения резервуара угол опережения (на самом деле — отставания) центра масс жидкости определяется формулой
αж = arctg((l / (2 · δ)) · (Δ – 1) / R) = arctg((Δ – 1) · k / 2) (4),
где α — угол опережения центром масс точки отсчёта; Δ — доля заполнения резервуара, от 0 до 1 (0...100%).
Угол опережения центра масс груза описывает формула
αг = arctg((l / δ) · (Δ — 0.5) / R) = arctg((Δ – 0.5) · k)) (5).
При этом квадрат расстояния от оси вращения колеса до центров масс жидкости и груза будет определяться соответственно формулами
Rж2 = R2 + (L · (Δ – 1) / 2)2 (6) и
Rг2 = R2 + (L · (Δ – 0.5))2 (7).
Теперь смотрим полученные графики изменения текущего момента и суммарной нормированной работы для этой конструкции.
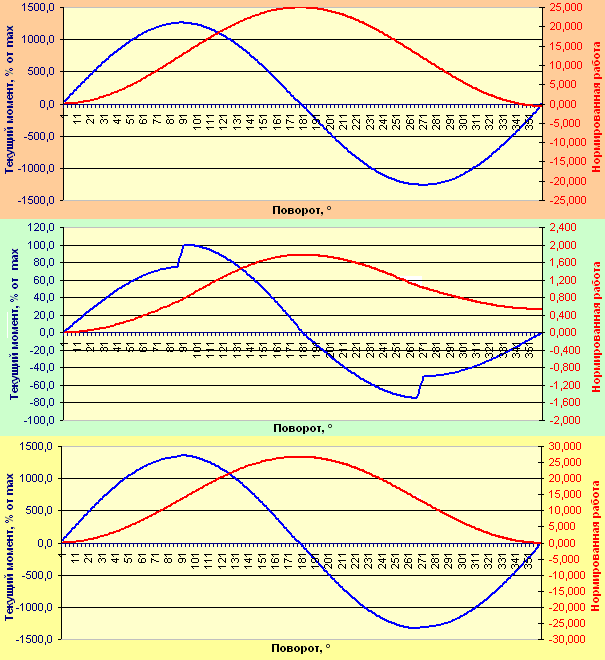 Текущий момент и суммарная нормированная работа одного элемента колеса с фиксированным краном при соотношении длины резервуара к радиусу вращения 10%, радиуса резервуара к радиусу вращения 5%, объёме одной порции 25% от полного объёма резервуара и передаче порции за время, необходимое для поворота колеса на 5°.
Нормированная работа за цикл груза одного элемента: -0,601744.
Нормированная работа за цикл жидкости в одном элементе: 0,533121.
Суммарная нормированная работа за цикл одного элемента: -0,068623.
Результат отрицательный... Однако, изменение параметров показывает, что если резервуар всё больше удалять от оси вращения (при этом расчёт массы приближается к формуле (1)) отрицательные значения потихоньку превращаются в положительные. Вот таблица для различных соотношений длины резервуара (по горизонтали) и его радиуса (по вертикали) к радиусу вращения при объёие порции 25%:
| |
10% |
1% |
0,1% |
| 5% |
-0,068623 |
0,010893 |
0,018844 |
| 1% |
-0,045700 |
0,030378 |
0,037986 |
| 0,1% |
-0,040542 |
0,034762 |
0,042292 |
С другой стороны, прямое применение для расчёта массы груза вместо формулы (3) формулы (1) даёт очень заметный положительный выход, когда резервуар находится близко к оси вращения, однако по мере удаления резервуара результаты становятся хуже, хотя по-прежнему положительные. Тем не менее, положительные результаты в таблице — лишь следствие упрощения расчёта, а даже не результат погрешности вычислений. Дело в том, что при вычислении массы груза предполагалось, что резервуар всё-таки находится достаточно близко к оси вращения, и угловое перемещение поршня относительно центра вращения превышает угол, в котором происходит коммутация резрвуаров. Однако, когда резервуар относительно невелик и находится далеко от оси вращения, наихудшим вариантом является не конец, а начало коммутации, потому что тогда уровень жидкости в левом резервуаре ниже, чем в конце передачи порции! Тогда в расчёт массы груза добавляется ещё одно слагаемое (выделено красным):
M = (1 + k · (2 · δ - 0.5) + r / R + sin(α)) · m / k (8),
где α — опережение угла начала коммутации относительно горизонтального положения элемента (в нашем случае — 5°).
В результате масса необходимого груза становится больше, его отрицательная работа возрастает и суммарная работа уменьшается. Впрочем, и 3% от перемещения резервуара размером в 1% от радиуса вращения — это практически ничего: ведь при радиусе вращения в 1 м радиус и длина резвуара будут равны 1 см.
Один из тонких моментов — при расчёте принято предположение о том, что центр масс поршня находится на границе жидкости в резервуаре. Удаление его от этой границы увеличивает отрицательную работу груза. Тем не менее, такое положение центра масс поршня можно обеспечить и без использования в качестве груза «бесконечно тонкой пластины из бесконечно тяжёлого вещества» — достаточно разместить груз снаружи резервуара в виде тяжёлого кольца, жёстко связав его с поршнем.
Другой тонкий момент — разные сочетания отношений r/R и L/R при прочих равных условиях подразумевают различные плотности жидкостей. На самом деле диапазон плотностей реальных жидкостей не очень широк: самая тяжёлая жидкость — это ртуть, а плотности менее экзотических и более безопасных жидкостей обычно близки к плотности воды.
Можно попытаться сместить фазы 3 и 7 назад, растянув «выгодные» фазы 4 и 8 и сократив «балластные» фазы 2 и 6. При смещении на 10° и даже на 20° наклон резервуаров в фазах 1 и 5 будет не столь существенен, чтобы вес их грузов обеспечил заметное противодействие перемещению жидкости, и в то же время вес грузов элементов в фазах 3 и 7 по-прежнему почти полностью будет работать на перекачку жидкости. Однако при этом существенно возрастёт разность уровней, которую необходимо преодолеть, а следовательно, также существенно вырастет и масса грузов и их отрицательная работа, которая снова «съест» всю прибавку полезной работы...
Самостоятельные расчёты для различных сочетаний параметров можно выполнить с помощью таблицы Excel, находящейся в zip-архиве. Изменяемые параметры (соотношение радиуса резервуара и радиуса вращения r/R, объём одной порции жидкости dM и отношение длины резервуара к радиусу вращения L/R, всё в %) находятся в белых полях верхней (зелёной) строки. В таблице использована формула (3); для расчёта по формуле (8) в ячейку E4 следует записать «=(1+G$1/100*(2*E$1/100-0,5)+C$1/100+SIN(ПИ()*5/180))*100*(100/(2*E$1)+100/G$1)». Внимание! Если соотношение размеров резервуара к радиусу вращения может быть практически любым, то объём порции более 50% физического смысла не имеет! Графики и результирующие данные — внизу таблицы.
Модифицированный вариант
Тем не менее, всё-таки рассмотрим модифицированный вариант конструкции.
Конструкция модифицированного варианта
В модифицированном варианте рабочие элементы аналогичны элементам модифицированной Архимедовой мельницы, только там они газонаполненные (поплавки), а здесь водонаполненные, однако всё, сказанное там относительно простоты конструкции, использование эффекта рычага при воздействии груза на изменение объёма и снижение за счёт этого массы груза, а также эффективности использования объёма колеса остаётся в силе и здесь.
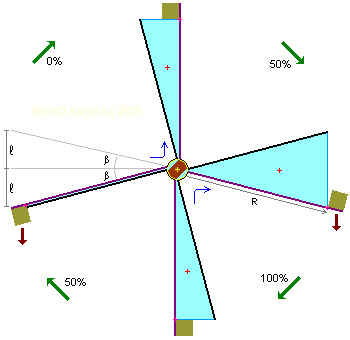
Модифицированное водяное колесо с фиксированным краном. R — расстояние от оси вращения до центра масс груза, β — половина полного угла раскрытия элемента (угол раскрытия элемента при приёме или передаче 50% жидкости), l — тангенциальное перемещение груза при удалении / добавлении одной порции жидкости (на рисунке — 50%). Коричневым обозначена неподвижная сердцевина крана, вокруг которой вращается внешний тонкий жёлтый корпус с жёстко прикреплёнными к нему резервуарами. Жёлтый крестик обозначает ось вращения конструкции, красные крестики — положение центров масс жидкости, розовые — центров масс грузов. Чёрные цифры указывают процент заполнения резервуара на соответствующем сегменте траектории элемента.
Совершенно нецелесообразно использовать лишь часть жидкости — ведь тогда остальная её часть превращается в бесполезный балласт. Поэтому объём одной порции должен быть равен 50%. Кстати, это сразу решает проблему точной дозировки порции — в одном случае (справа) её ограничивает максимальный объём элемента, а в другом (слева) — исчерпание жидкости в элементе.
Помимо изменения конструкции элемента, изменена и конструкция крана — теперь в его корпусе нет трудных в изготовлении каналов, просверленных под точным углом, а есть лишь две лыски, которые способен разметить и сделать с помощью напильника любой аккуратный человек, имеющий минимальные слесарные навыки. После сборки крана эти лыски и образуют необходимые каналы.
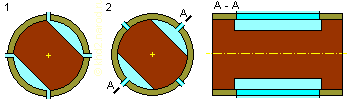
Модифицированная конструкция крана. 1 — кран в открытом состоянии (элементы соединены друг с другом). 2 — кран в закрытом состоянии (элементы заперты). A-A — продольный разрез крана. Более тёмным обозначена неподвижная сердцевина крана, вокруг которой вращается более светлый внешний тонкий корпус с жёстко прикреплёнными к нему резервуарами. Жёлтым цветом обозначена ось вращения конструкции.
Хотя в запертом состоянии только половина резервуаров отключена от полостей корпуса крана, подключённые к полостям резервуары также заперты, поскольку подключены каждый к своей полости, размеры которых, а следовательно и объём жидкости в них в запертом измениться не могут. Угловой размер полости должен быть равен 90° + α - γ, где α — угол, в пределах которого должна осуществляться коммутация соседних резервуаров, а γ — угловой размер каналов в подвижном корпусе крана. Для обеспечения максимальной скорости передачи жидкости каналы предполагаются в виде щелей, которые соответствуют достаточно протяженным вдоль оси рабочим элементам и которые достаточно легко прорезать в тонком корпусе-трубке крана.
Расчёт модифицированного варианта
Если угол поворота конструкции α, в котором осуществляется коммутация элементов, не превышает угол изменения элемента при передаче порции жидкости β, то высота столба жидкости, давление которого должен преодолеть груз, на рабочем ходе (в фазе 3, элемент опускается и увеличивает свой объём до полного) должна быть равна R · (cos(β) + sin(α)) в начале перекачки жидкости и R · (cos(β) - sin(β)) в конце, и на обратном ходе (в фазе 7, элемент поднимается и выкачивает всю жидкость в верхний элемент) — R · (cos(β) + sin(α)) в начале фазы перекачки и R · (cos(β) + sin(β)) в конце. Здесь подразумевается, что фаза завершается при строго горизонтальном положении точки отсчёта, соответствующей геометрическому центру полностью раскрытого элемента, α — отклонение угла, при котром начинается фаза перекачки, от горизонтального положения, α — изменение угла раскрытия элемента при передаче одной порции жидкости (50% от полного объёма резервуара. Таким образом, худшим вариантом является R · (cos(β) + sin(α | β)) (синус следует брать от того из углов α или β, который будет больше с учётом конкретных геометрических размеров). Итак, чтобы вес груза преодолел неизбежную разность давлений, его масса должна быть равна
M = R · (cos(β) + sin(α)) · g · ρ · S / g = R · (cos(β) + sin(α)) · ρ · S (9),
где ρ — плотность жидкости, g — ускорение свободного падения; S — площадь подвижной стороны резервуара.
Впрочем, поскольку у нас подвижная сторона (крышка) резервуара с одной стороны закреплена на шарнире, она представляет собой рычаг, где груз имеет максимальное плечо. Поэтому с учётом плеча давления, равномерно распределённого по всей длине крышки масса груза требуется вдвое меньше. Учитывая это замечание, а также то, что площадь прямоугольной крышки S = R · d (где d — длина резервуара вдоль оси вращения) и что масса жидкости в полностью (100%) раскрытом резервуаре равна m = 2 · (R · cos(β) · R · sin(β) · d / 2) · ρ = S · R · cos(β) · sin(β) · ρ, то, выразив с учётом этого соотношения площадь в формуле (9) получаем отношение массы груза к массе жидкости равным
M = (R · (cos(β) + sin(α)) · ρ · m / (R · cos(β) · sin(β) · ρ)) / 2 = m · (cos(β) + sin(α)) / (2 · cos(β) · sin(β)) (10),
где в случае, если угол изменения раскрытия резервуара β превышает угол отклонения начала фаз перекачки от горизонтали α, sin(α) следует заменить на sin(β).
На самом деле масса нужна ещё меньше, поскольку давление взято для худшего случая на дальней стороне крышки, а возле оси оно немного меньше, но зато мы пренебрегли и небольшим усилием, необходимым чтобы чуть приподнять груз вертикального элемента при его раскрытии... Так что это вполне может дать небольшую погрешность в расчётах в ту или иную сторону — но, при условии, что полный угол раскрытия элемента не превышает 10–15°, лишь небольшую погрешность, которая не даст сколько-нибудь практически значимого изменения рассчитанной работы!
Центр масс груза от оси вращения всегда находится на расстоянии R, а центр масс жидкости в резервуаре в соответствии с геометрически центром его треугольного бокового сечения — на расстоянии 2/3 R (66%).
Угол опережения точки отсчёта центром масс груза в зависимости от заполнения резервуара равен
αг = 2 · β · Δ – β = β · (2 · Δ – 1) (11),
где α — угол опережения центром масс точки отсчёта; β — изменение угла раскрытия резервуара при передаче одной порции жидкости (половина полного угла раскрытия); Δ — доля заполнения резервуара, от 0 до 1 (0...100%).
В свою очередь, угол опережения точки отсчёта центром масс жидкости равен
αж = 1 – β · Δ (12).
К сожалению, результаты расчётов (вторая страница таблицы в zip-архиве) совершенно неутешительны — для порции в 50% и угла изменения раскрытия 7,5° (полный угол раскрытия резервуара — 15°) получено:
Нормированная работа за цикл груза одного элемента: -1,080963.
Нормированная работа за цикл жидкости в одном элементе: 0,687992.
Суммарная нормированная работа за цикл одного элемента: -0,392971.
Чем можно объяснить столь заметное ухудшение нормированной работы — от чуть-чуть отрицательной для исходного варианта до существенно отрицательных значений в модифицированном варианте? Всё дело в треугольной геометрии элементов — если в исходном варианте вес груза прямо пропорционален разности давлений, то здесь, по мере приближения к оси вращения, благодаря свойствам рычага необходимый вес груза уменьшается линейно, а полезная работа от жидкости — в квадратичной пропорции (пропорционально рычагу и пропорционально уменьшаемому сечению). Отсюда относительно избыточный вес груза и общее ухудшение результатов.
Так что анализ модифицированном варианта даёт однозначный вывод — в этой конструкции резервуар должен быть сделан таким образом, чтобы его сечение не менялось! Зато конструкция крана впоне применима и к исходному варианту.
Если будут обнаружены ошибки в кинематике, в формулах или алгоритме расчёта, буду благодарен за замечания.
♦
|