Архимедова драга

Это необычный и остроумный проект описанный в статье В.И.Богомолова. Он использует тот факт, что сила Архимеда действует на поплавок только тогда, когда жидкость имеет свободный доступ к его нижней поверхности. Если этот доступ перекрыть, то поплавок всплывать не будет, даже если его плотность намного меньше плотности окружающей жидкости, а значит, можно попытаться погрузить его, не затрачивая работы на преодоление силы всплытия...

В.И.Богомолов назвал это устройство «драга Архимеда». Однако, хотя в его работе вовсю используется сила Архимеда, сам Архимед к его изобретению отношения не имеет. Поэтому я предпочитаю называть его «архимедовой драгой» — с маленькой буквы.

Эффект подавления всплытия
Устройство архимедовой драги
Расчёт архимедовой драги

Эффект подавления всплытия

Рассмотрим тело (поплавок) в толще жидкости. Для упрощения предположим, что оно имеет форму прямоугольного параллепипеда, как на рисунке внизу. Его самые большие грани расположены горизонтально и равны по площади. Как известно, сила, с которой жидкость давит на каждую его грань, равна произведению давления на площадь этой грани и направлена внутрь тела. Cилы давления жидкости на боковые грани взаимно компенсируются, а силы давления на верхнюю F_В и нижнюю F_Н грани различаются из-за разницы глубин, на которых они находятся. При этом сила давления F_Н всегда больше F_В, поскольку нижняя грань находится глубже и давление там выше. Возникает разница сил, выталкивающая тело вверх, и если она больше, чем его вес вне жидкости, то тело всплывёт. Итак, мы в очередной раз «открыли» закон Архимеда.

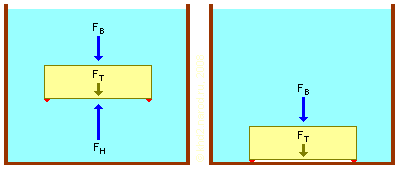Эффект подавления силы всплытия. Слева — поплавок в свободной жидкости, справа — доступ жидкости к нижней поверхности поплавка перекрыт (красным показано уплотнение). F_В — сила давления жидкости на верхнюю поверхность поплавка, F_Н — сила давления жидкости на его нижнюю поверхность, F_Т — сила тяжести, действующая на поплавок.

Однако что будет, если убрать давление на нижнюю грань? Ответ очевиден — поплавок уже не будет всплывать, а к силе тяжести, тянущей его вниз, добавится ещё и сила давления столба воды над ним F_В. Как добиться этого? Например, герметично прижать его к дну резервуара с жидкостью, — так, чтобы жидкость не могла проникнуть в щель между дном резервуара и нижней поверхностью поплавка. Этот эффект используют самые обыкновенные присоски, скажем, для мыльницы в ванной, правда там обычно имеют дело не с жидкостью, а с газом (воздухом). Разновидность этого эффекта обуславливает и «засасывание» при определённых условиях даже относительно лёгких вибрирующих тел в вязких жидкостях, в том числе в болотных трясинах и зыбучих песках.

Как восстановить плавучесть поплавка? Достаточно нарушить герметичность уплотнения или открыть специальный кран, соединяющий эту щель с жидкостью вне поплавка — жидкость хлынет в полость, давление на нижнюю поверхность поплавка уравняется с давлением на этой глубине вне его, закон Архимеда заработает в полную силу, и поплавок всплывёт!

Каждый может убедиться в реальности этого эффекта самостоятельно, однако при проведении опытов следует обратить внимание на три момента. Во-первых, поплавок-присоску следует крепить именно ко дну резервуара или какому-либо тяжёлому предмету на его дне — если его прикрепить к лёгкой пластинке, то он всплывёт вместе с ней, поскольку теперь роль нижней поверхности поплавка будет играть эта пластинка, а её веса недостаточно, чтобы утонуть самой вместе с поплавком. Во-вторых, корпус поплавка должен обладать достаточной прочностью (или упругостью), чтобы его не расплющило давлением воды, и он не потерял необходимую плавучесть и в то же время не пропустил воду внутрь раньше, чем надо (лопнувший воздушный шарик не подойдёт — его просто «размажет» по дну). В-третьих, качество уплотнения должно быть очень хорошим — для этого можно использовать резиновый, силиконовый или другой уплотнитель либо сопрягать «всухую» шлифованные поверхности типа притёртого стекла (это, конечно, выглядит более эффектно). Даже кажущиеся ровными края обычного стакана или чашки и дно кастрюли на самом деле имеют множество микронеровностей, которых достаточно для того, чтобы вода проникла внутрь стакана и испортила опыт. Но если край стакана обильно смазать густым маслом, прижать его ко дну кастрюли и затем осторожно заполнить кастрюлю водой, опыт вполне может удасться — стакан будет оставаться на дне кастрюли, а если его сдвинуть пальцем, то он подвсплывёт, перевернётся, выпустит пузырь воздуха и снова утонет — на этот раз окончательно...

Устройство архимедовой драги

Идея архимедовой драги заключается в следующем. Если работа по утоплению поплавка компенсирует работу от его всплытия, то надо попытаться устранить работу потопления, оставив одну работу всплытия. Тут-то и можно применить описанный выше эффект подавления всплытия, для чего поплавок на воздухе надо герметично прижать скошенной нижней гранью к ровному откосу, установленному под тем же углом, что и скос нижней грани. По этому откосу поплавок съедет в воду до нужной глубины. Там к его нижней поверхности подаётся жидкость, начинает работать закон Архимеда, он всплывает и по поверхности вновь возвращается к откосу, как показано на рисунке.

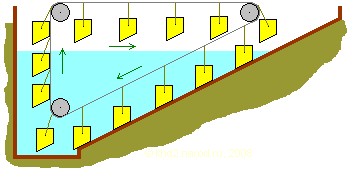Устройство архимедовой драги.

Здесь предполагается совместная работа двух сил — силы Архимеда на участке вертикального подъёма и силы тяжести вкупе с силой давления водяного столба на участке скольжения по откосу, которые также должны способствовать движению поплавка в нужном нам направлении.

С технической точки зрения самым сложным является обеспечение хорошего уплотнения, в то же время не препятствующего скольжению поплавков вниз по откосу. Для подачи жидкости к нижней поверхности поплавка достаточно создания любой неровности на откосе (щели, уступа и пр.), нарушающей герметичность этого уплотнения. Ориентация поплавков важна только при их движении вдоль откоса, на остальных участках пути в соответствии с законом Архимеда играет роль лишь их объём. Обратную ветвь необязательно поднимать над поверхностью жидкости, поскольку роль играет лишь разность уровней между точкой «пристыковки» поплавка к откосу (или начала его погружения по откосу) и точкой его отрыва от откоса. Но если поплавок «пристыковывать» к откосу под поверхностью жидкости, то технически сложнее в начале его движения по откосу предотвратить доступ жидкости к нижней поверхности поплавка и удалить ту жидкость, которая уже имеется там в момент касания.

Вроде бы всё складывается в нашу пользу и нет видимых причин, которые могут остановить цепь поплавков. Но прежде чем достать инструменты, засучить рукава и приступить к изготовлению натурного образца, всё-таки проверим работоспособность драги расчётом на бумаге (то бишь на экране).

Расчёт архимедовой драги

Итак, посчитаем работу от одного поплавка за рабочий цикл — как обычно, пока без учёта потерь на трение и сопротивление среды. Для упрощения расчётов будем рассматривать прямоугольный поплавок с горизонтальной верхней гранью и скошенной нижней.

Верхняя ветвь цепи, возвращающая поплавки к откосу, горизонтальна и потому не изменяет потенциальную энергию поплавков. Связанные цепью поплавки в установившемся режиме работы движутся с постоянной скоростью, так что их кинетическая энергия в течение рабочего цикла тоже не меняется. Остаётся лишь проанализировать работы поплавков на двух участках — работу всплытия с глубины отрыва от откоса и работу поплавка при погружении по откосу. При этом работы силы тяжести (изменение потенциальной энергии) при погружении и всплытии взаимно компенсируют друг друга, и можно рассматривать лишь работу, вызванную силами давления жидкости на поверхности поплавка.

Работа всплытия с глубины отрыва h в соответствии с законом Архимеда вычисляется по формуле

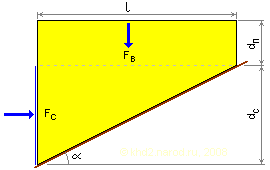Расчёт поплавка архимедовой драги. l — длина поплавка (длина его верхней грани в направлении вдоль откоса), d_п — высота прямоугольной части поплавка, d_с — высота скошенной части поплавка, α — угол скоса днища поплавка относительно горизонтали, F_В — сила давления воды на верхнюю поверхность поплавка, F_с — нескомпенсированная сила давления воды на переднюю поверхность скошенной части поплавка.

В свою очередь, при погружении по откосу работа определяется силами давления воды на верхнюю поверхность поплавка и нескомпенсированного давления на переднюю поверхность скошенной части.

Сила давления столба воды, действующая на верхнюю поверхность поплавка, направлена под углом к поверхности откоса, поэтому образуется её составляющая, стремящаяся сдвинуть поплавок вдоль откоса в нужном нам направлении, которая численно равна

Сила, действующая на переднюю поверхность скошенной части, стремится остановить поплавок и вредна для нас. Она равна

Из формул (2) и (3) следует, что F_Д = F_С, а следовательно, они взаимно компенсируют друг друга и нескомпенсированной остаётся лишь полезная сила Архимеда F_А на участке всплытия. Однако в действительности это не совсем так. Дело в том, что скошенная часть расположена несколько ниже верхней поверхности поплавка, а значит давление там чуть больше из-за большей глубины. Поэтому мы должны прибавить к глубине верхней поверхности поплавка всю высоту его прямоугольной части d_п и половину высоты скошенной части d_c (поскольку точка приложения суммарного давления на скошенную часть находится в геометрическом центре её передней поверхности). Этот аспект кажется очень незначительным, однако для строгой корректности расчёта его всё же необходимо учесть. В результате формула (3) приобретает следующий вид:

Равнодействующая этих сил, направленная вдоль поверхности откоса, равна

Сразу обратим внимание на два момента. Во-первых, равнодействующая сила при движении по откосу имеет отрицательный знак и потому является тормозящей, вредной для нас — добиться дополнительного выигрыша при погружении не удалось, не потерять бы полученное при всплытии! Во-вторых, чем выше прямая часть поплавка, тем больше эта вредная для нас сила, поэтому в идеале боковой профиль поплавка должен иметь треугольную форму — чтобы обеспечить минимальную разность давлений на его верхнюю поверхность и середину передней поверхности скошенной части. Впрочем, при этом соответственно уменьшится выигрыш во время всплытия поплавка под действием силы Архимеда.

Теперь посчитаем работу, которую нам необходимо затратить на погружение поплавка. Путь, который должен пройти поплавок, погружаясь по откосу под углом α на глубину h, равен   L = h / sin(α).   Поэтому работа на погружение равна

Сравниваем только что полученную формулу затрат работы на погружение (6) с формулой для работы силы Архимеда (1) и видим их полную идентичность — и в этот раз затраты на погружение оказались равны выигрышу от всплытия, а потому, как и в случае с другими цепями поплавков, дополнительной работы получить не удалось! Тем не менее, нельзя не отметить оригинальность самой идеи — попытаться погрузить поплавок без затрат работы. К сожалению, вроде бы незначительная разность давлений (всего лишь в пределах части высоты поплавка!) сыграла с нами злую шутку и ещё раз напомнила, что в науке и технике мелочей не бывает... ♦