Идеальный вечный двигатель типа «мельница»

На этой странице мы проанализируем два крайних идеальных случая — обычное колесо и идеальный механический вечный двигатель с круговым движением. Поскольку такие конструкции по сути обыгрывают принцип водяной мельницы, колесо которой вращается благодаря разности моментов силы на рабочей стороне, куда льётся поток воды, и на противоположной стороне обратного хода, свободной от такой нагрузки, то их иногда называют «мельницами», хотя, конечно, они ничего не молотят. Я тоже время от времени использую этот термин.

Вращение обычного колеса
Идеальный вечный двигатель с круговым движением

Вращение обычного колеса

Прежде чем начинать изобретать, стоит рассмотреть, как ведёт себя самое обычное колесо, поставленное вертикально и вращающееся вокруг горизонтальной оси. Предположим, что практически вся масса сосредоточена в его ободе, а трение в подшипнике на оси очень мало (среди реальных устройств к такой модели очень близко переднее велосипедное колесо — без трещёток и тормозов). Хотя в таком колесе нет дискретных элементов, в качестве рабочего элемента можно рассмотреть любой достаточно малый кусочек сплошного обода (число таких элементов, соответственно, будет равно отношению длины этого кусочка к общей длине обода колеса). Эквивалентной моделью такого рабочего элемента будет груз, вес которого равен весу выбранного кусочка обода, вращающийся в вертикальной плоскости вокруг шарнира на жёстком рычаге, длина которого равна радиусу колеса — именно то, что рассматривалось при знакомстве с вращающим моментом.

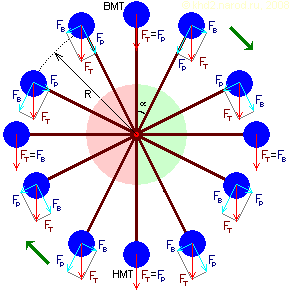Круговое вращение груза в вертикальной плоскости. F_T — вес груза, F_P — сила, с которой рычаг воздействует на шарнир (компенсируется силой реакции опоры шарнира благодаря жёсткости рычага), F_В — нескомпенсированная поворачивающая сила, R — расстояние от шарнира (оси поворота) до траектории центра масс груза. Зелёным показана область ускорения, а красным — торможения груза.

Как видно из рисунка, ровно половину рабочего цикла груз ускоряется, двигаясь из верхней мёртвой точки (ВМТ) в нижнюю мёртвую точку (НМТ), а другую половину — тормозится при обратном движении. Если бы не было потерь на трение и сопротивление среды, он мог бы вращаться вечно, но, к сожалению, в реальной жизни так не бывает. Тем не менее, расчёт для идеального случая показывает нулевую суммарную работу.

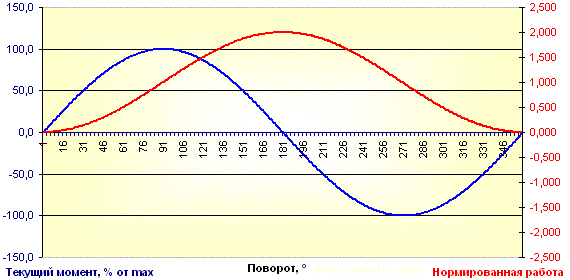Текущий момент и суммарная нормированная работа груза при равномерном круговом движении в вертикальной плоскости вокруг неподвижной оси (элемент обода обычного колеса).
Нормированная работа за цикл от одного элемента: -0,000000.

Подробная таблица пошагового изменения моментов для равномерного кругового движения cама по себе не представляет большого интереса, однако является своего рода эталоном при сравнении с аналогичными таблицами для других конструкций, позволяя сразу видеть, где они выигрывают, а где проигрывают по сравнению с обычным колесом.

Идеальный вечный двигатель с круговым движением

Итак, в случае с обычным колесом всё портит обратный ход — возвращение от НМТ к ВМТ. Поэтому логично предположить, что в идеальном механическом вечном двигателе следует не просто что-то сделать с обратным ходом, а вообще устранить его, — так, чтобы груз каким-либо чудесным образом переходил из НМТ в ВМТ без затрат энергии.

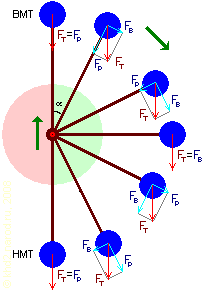Траектория перемещения груза для идеального вечного двигателя типа «мельница». F_T — вес груза, F_P — сила, с которой рычаг воздействует на шарнир (компенсируется силой реакции опоры шарнира благодаря жёсткости рычага), F_В — нескомпенсированная поворачивающая сила. Зелёным показана область ускорения, а красным — торможения груза.

Чуть более технически реальным по сравнению со скачком из НМТ в ВМТ (при том же суммарном результате) является организация перемещения груза в начале обратного хода из НМТ в центр конструкции, а в начале рабочего хода — из центра в ВМТ. В этом случае из-за нулевого плеча за время обратного хода груз не совершит никакой отрицательной работы, в то же время не потребуется скачкообразного изменения скорости и направления вращения всей конструкции в целом — об этом нельзя забывать, если предполагается составлять её из нескольких однотипных элементов. Вся беда в том, что и здесь вернуть груз на исходную позицию без затрат энергии вряд ли удастся — ведь для этого необходимо совершить работу против силы тяжести!

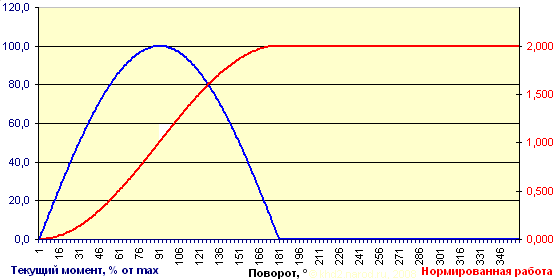Текущий момент и суммарная нормированная работа груза в идеальном механическом двигателе типа «мельница».
Нормированная работа за цикл от одного элемента: 1,999949.

Полученное значение суммарной нормированной работы за вычетом погрешностей, неизбежных при использовании численных методов, равно 2. А это как раз и есть работа, которую может совершить единичный груз в однородном потенциальном поле, опустившись на величину диаметра, т.е. на удвоенный единичный радиус. Большей отдачи при использовании лишь одной гравитации (силы тяжести или силы Архимеда) получить невозможно в принципе, так что двигатель с такой схемой движения груза действительно являлся бы идеальным, вот только вернуть груз из НМТ в ВМТ без затрат энергии пока ещё никому не удавалось!

Подробная таблица пошагового изменения моментов для идеального перемещения груза в механическом гравитационном вечном двигателе в точности совпадает с первой половиной таблицы для обычного колеса, и также представляет интерес лишь как эталон для сравнения с аналогичными таблицами для других конструкций.

P.S. Всё вышесказанное представляется безусловно верным при попытке использовать одну лишь силу тяжести, поскольку в обычных условиях ни изменить её направление, ни экранировать не представляется возможным. Однако, не в последнюю очередь благодаря В.И.Богомолову, мне пришлось обратить пристальное внимание на центробежные силы, которые являются одним из проявлений инерции и во многих случаях действуют на вращающиеся тела подобно гравитационным, — в частности, они воздействуют распределённо на весь объём вещества, а не на на одну его точку или поверхность. Но в отличие от гравитации, изменить величину центробежных сил достаточно просто — при одной и той же скорости вращения приближение к центру вращения уменьшает центростремительное ускорение, а удаление от центра увеличивает его. Для того, чтобы вообще убрать их воздействие на тело, необходимо лишь вывести его из вращательного движения.

Однако при работе с центробежными силами следует обратить особое внимание на два момента. Во-первых, система отсчёта, связанная с вращающимся телом, является неинерциальной, и не все расчёты, применимые для инерциальных систем, можно переносить туда без существенной коррекции. Во-вторых, чем дальше от центра, тем больше кинетическая энергия вращающейся массы, а чем ближе к центру — тем она меньше. Поэтому нельзя считать, что можно просто взять медленно движущееся тело возле центра вращения, переместить его на периферию и черпать из этого море энергии — чтобы быть полноценно вовлечённым во вращение, на периферии тело должно разогнаться до скорости, соответствующей скорости вращения системы, а на это, очевидно, требуется затратить немало энергии. И всё-таки, во всех успешных конструкциях «вечных двигателей» в широком смысле этого слова, в которых в той или иной форме используется механическое движение и упоминания о которых можно считать хоть сколько-нибудь правдоподобными — от «Тестатики» и дисков Сёрла до двигателей Клема и Шаубергера, — использовалось достаточно быстрое вращение. Впрочем, я считаю, что и в этих случаях само вращение является не первичной причиной их работы, а лишь средством для достижения этого... ♦