Колесо в магнитной жидкости

Очень необычная идея, любезно присланная мне одним из посетителей сайта, Денисом (@-mail: rootsky на inbox.ru). Её изюминка заключается в том, что при использовании эффекта Архимеда автор попытался создать дисбаланс сил для немагнитных поплавков, сместив магнитную жидкость в сторону от вертикали с помощью магнита и направив действие силы всплытия не строго против силы тяжести, а под углом к ней.

Хотя в этой конструкции и используется магнит, я однозначно отношу её не к магнитным, а к механическим устройствам, поскольку магнит установлен неподвижно и его магнитное поле, как и общее положение магнитной жидкости, во время работы никак не меняется. Более того, при некоторой технической изощрённости без ущерба для идеи можно заменить магнитные силы другими — скажем, попробовать создать электретную жидкость и воздействовать на неё электростатическим полем... Наконец, можно сместить жидкость чисто механически — за счёт центробежных сил, — однако при этом надо выбирать ось вращения (не колеса, а всей конструкции в целом) так, чтобы с одной стороны (где нет жидкости) на поплавки воздействовала практически лишь одна сила тяжести, а на стороне, в которую перемещается жидкость, воздействие центробежных сил было бы ощутимым — описание именно такой конструкции почти одновременно с Денисом и абсолютно независимо от него прислал В.И.Богомолов. Замечу, что последний вариант выгодно отличается тем, что позволяет вместо экзотических магнитных жидкостей, как правило достаточно густых и малотекучих, использовать любые обычные жидкости — в том числе и с небольшим вязкостным сопротивлением движению поплавков.

Принцип работы конструкции
Анализ конструкции
Модификация конструкции

Принцип работы конструкции

Исходная идея заключалась в следующем. Жёсткая цепь немагнитных твёрдых поплавков находится в сосуде, большая часть которого заполнена средой с малой плотностью (менее плотной, чем поплавки). Однако некоторая часть его объёма заполнена магнитной жидкостью, плотность которой выше плотности поплавков, и которая под воздействием внешнего постоянного магнитного поля смещена в сторону относительно середины сосуда. Все прочие элементы конструкции выполнены из немагнитных материалов. В половине сосуда, свободной от магнитной жидкости, на поплавки действует только сила тяжести, а в половине с магнитной жидкостью добавляется действие силы Архимеда. В результате предполагается получение дисбаланса сил, обеспечивающего вращение колеса.

Заменим жёсткую цепь поплавками, насаженными на прочные спицы — это упрощает конструкцию и гарантирует стабильную траекторию их движения. В качестве немагнитной среды с малой плотностью вполне подойдёт самый обыкновенный воздух, немагнитные поплавки можно изготовить из твёрдого пенопласта средней плотности, а немагнитное колесо взять алюминиевое или пластиковое. Магнитным жидкостям и их изготовлению на сайте посвящена отдельная страница. В результате у нас получилась конструкция, изображённая на рисунке.

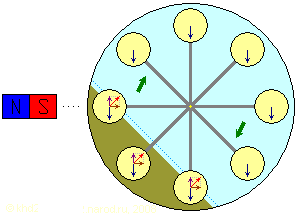Принцип работы колеса с поплавками в магнитной жидкости. Светло-голубым показана среда с малой плотностью (воздух), светло-желтым — поплавки, жёлто-коричневым — магнитная жидкость. Голубым пунктиром отмечен уровень колебания жидкости при погружении в неё поплавков.
На рисунке показан случай для достаточно далеко расположенного мощного магнита (силовые линии магнитного поля в области колеса параллельны друг другу, воздействие магнитного поля на магнитную жидкость направлено перпендикулярно силе тяжести и по величине равно ей). Синей стрелкой обозначена сила тяжести, фиолетовой — выталкивающая сила, обусловленная гравитацией, коричневой — выталкивающая сила, обусловленная магнитными силами, красной — результирующая выталкивающая сила.

Анализ конструкции

Для большей наглядности анализа предположим пока, что магнит, смещающий жидкость, расположен достаточно далеко, чтобы линии его магнитного поля во всей области, занимаемой нашим колесом, были параллельны друг другу, а сила притяжения во всём объёме магнитной жидкости была практически одинакова и по своему направлению перпендикулярна силе тяжести. Однако при этом мощность магнита достаточно велика, чтобы его воздействие на магнитную жидкость по величине было равно силе тяжести. Очевидно, что под воздействием двух взаимно перпендикулярных, равномерно распределённых в пространстве и равных по величине сил магнитная жидкость займёт положение под углом в 45° относительно гравитационной и магнитной горизонталей (также взаимно перпендикулярных друг другу). Именно такая ситуация и показана на верхнем рисунке.

Рассмотрим силы, действующие на поплавок в этом случае. Их две — это сила тяжести на всей траектории движения и сила Архимеда на участке прохождения магнитной жидкости. Сила тяжести действует неизменно и потому на круговой траектории её воздействие полностью компенсирует само себя. Остаётся лишь сила Архимеда (точнее, чистая выталкивающая сила — без силы тяжести, которую мы уже учли), с ней и разберёмся более подробно.

На рисунке наглядно видно, что результирующая выталкивающая сила, являющаяся векторной суммой выталкивающих сил, вызванных гравитационным и магнитным полями, в нашем случае будет постоянна (за исключением моментов входа колеса в жидкость и выхода из неё) и направлена перпендикулярно поверхности магнитной жидкости по направлению к оси вращения колеса. На этапе погружения колеса в жидкость (нижняя часть траектории) она тормозит предполагаемое движение и является вредной, в момент прохождения самого «глубокого» места под углом в 45° направлена строго к центру колеса и полностью компенсирована реакцией опоры (т.е. спицы, на которой укреплён поплавок, и оси колеса), а при всплытии поплавка (выше угла в 45°) способствует движению поплавка в нужную нам сторону и является «полезной». К сожалению, не менее наглядно на рисунке видно, что участок погружения является зеркальным отражением участка всплытия, а следовательно, «полезная» и «вредная» работы выталкивающей силы равны друг другу и взаимно скомпенсированы. Так что никакого выигрыша в работе и энергии нам опять получить не удалось...

Кстати, интересное замечание — куда вытесняется магнитная жидкость при погружении в неё поплавка, — вверх или вниз? Ответ таков — при погружении в жидкость тела, её уровень повышается относительно эквипотенциальной поверхности, образованной под суммарным воздействием всех объёмных сил, то есть в нашем случае жидкость будет вытесняться под углом 45° к центру сосуда, а относительно гравитационной горизонтали можно сказать, что она будет вытесняться и вверх, и вниз — на рисунке колебания её уровня обозначены пунктирной линией.

Тем не менее, мы рассматривали, мягко говоря, сильно идеализированную ситуацию. Попробуем рассмотреть более жизненные варианты — вдруг там обнаружится что-нибудь интересное?

Модификация конструкции

Приблизим конструкцию к реальности. Для этого, во-первых, сосуд совсем необязательно делать закрытым — достаточно лишь обеспечить бортики, не позволяющие магнитной жидкости покинуть сосуд под воздействием магнита (если только магнитная жидкость не содержит летучих компонентов, испарение которых нежелательно). Во-вторых, разместим магнит непосредственно у борта сосуда (как вариант, можно расположить его и внутри сосуда). В результате получим нечто подобное изображённому на рисунке внизу.

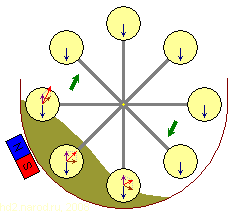Модифицированная конструкция колеса с поплавками в магнитной жидкости.
Синей стрелкой обозначена сила тяжести, фиолетовой — выталкивающая сила, обусловленная гравитацией, коричневой — выталкивающая сила, обусловленная магнитными силами, красной — результирующая выталкивающая сила.

Из-за того, что сила воздействия близкорасположенного магнита на магнитную жидкость определяется расстоянием до него от конкретной точки жидкости, жидкость выгнулась «горбом» напротив магнита. При этом участок погружения несколько удлинился, хотя «вредная» магнитная сила Архимеда там несколько уменьшилась, а участок всплытия сократился, но «полезная» магнитная сила Архимеда несколько выросла. Оба эффекта обусловлены именно зависимостью воздействия магнита на магнитную жидкость от расстояния.

Даст ли нам это желанный выигрыш? Сразу должен ответить: «нет!». Уменьшение средней выталкивающей силы на участке погружения точно компенсируется увеличением длины этого участка, а её повышение на участке всплытия — сокращением длины самого всплытия. Это объясняется тем, что форма поверхности жидкости определяется условием эквипотенциальности суммарного воздействия всех влияющих на неё сил (в нашем случае — гравитационных и магнитных). И работа при погружении (от поверхности до точки с наибольшим давлением жидкости) в точности равна работе всплытия (от точки с наибольшим давлением до поверхности), поскольку определяется лишь разностью давлений, а не формой пути. Проверим это математикой.

Рассмотрим классический случай — тело, погружённое в жидкость в гравитационном поле. В таком случае выталкивающая сила Архимеда (без учёта действия на тело силы тяжести) будет вычисляться по формуле

Соответственно, работа выталкивающей силы при подъёме тела с глубины  h  (или против этой силы при погружении на ту же глубину) будет равна

В то же время, давление на этой глубине определяется по формуле

С учётом формулы (3) формулу работы выталкивающей силы (2) можно преобразовать к виду

Итак, мы видим, что глубина (путь погружения) в формуле для работы выталкивающей силы отсутствует, если эту работу выражать через давление. И, с другой стороны, значение имеет лишь разность давлений, преодолеваемая при всплытии или погружении, а очевидно, что погружаясь от поверхности и возвращаясь к ней, тело проходит одну и ту же разность давлений, а значит работы погружения и всплытия взаимно компенсируются вне зависимости от того, как именно гравитационные, магнитные и прочие аномалии искажают поверхность жидкости. ♦