Колёса с грузами на рычагах
Свободно перемещающиеся грузы не принесли нам дополнительной энергии. Может быть, поможет принудительное перемещение грузов?
Колёсо с рычагами, откидывающимися наружу
Колесо с рычагами, складывающимися внутрь
Описание конструкции
Кинематика грузов
Фаза 1. Висящий груз
Фаза 2. Лежащий груз
Фаза 3. Груз в середине колеса
Расчёт конструкции
Колёсо с рычагами, откидывающимися наружу
Конструкции с принудительным перемещением грузов (прежде всего с помощью рычагов) ненамного младше конструкций со свободным перемещением грузов. Первое письменное упоминание о них встречается в арабских источниках и датируется 1206 годом. Там использовались ломанные рычаги из кусков доски. Но мы попробуем разобраться с более простой конструкцией, где рычаги лёгкие и жёсткие, а груз прикреплён к их концам.
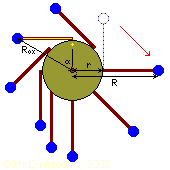 Колесо с грузами на жёстких откидывающихся рычагах. R — плечо груза в положении рабочего хода, Rox — плечо груза в положении обратного хода, r — радиус крепления шарниров рычагов, α — угол отставания груза от положения точки отсчёта. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта.
Рычаги с грузами крепятся к ступице колеса на шарнирах. Во время рабочего хода рычаг с грузом откидывается перпендикулярно к ободу колеса, обеспечивая максимальный вращающий момент. В начале обратного хода за счёт шарнирной подвески он начинает прижиматься к колесу до тех пор, пока это позволяют конструкция шарнира. При этом груз приближается к оси вращения колеса, и его вращающий момент уменьшается. Это должно создать разность моментов, обеспечивающую непрерывное вращение колеса. Что ж, проверим идею расчётом — выполняется ли основное условие успешной работы?
Трение, сопротивление среды и прочее в первом приближении можно не учитывать. Масса груза не изменяется. За точку отсчёта угла поворота возьмём шарнир рычага рассчитываемого элемента. В качестве базового радиуса R выберем расстояние от оси колеса до центра масс груза в положении рабочего хода — при максимально откинутом рычаге. Если обозначить расстояние от оси колеса до оси шарнира крепления рычага r, то при складывании рычага (начиная со 180°) плечо груза Rox и угол отставания груза от положения точки отсчёта α в соответствии с правилами решения треугольников следует рассчитывать по формулам
Rox2 = (r + Rр· cos(γ – 180°))2 + (Rр· sin(γ – 180°))2 (1.1)
α = arctg((Rр· sin(γ – 180°)) / (r + Rр· cos(γ – 180°))) (1.2),
где Rр= R – r — длина рычага, а γ — текущий угол поворота точки отсчёта.
Если принять r равным 20% от R (Rр= 80% от R), то параметры фаз движения можно записать в виде следующей таблицы (поскольку в расчёте участвует именно угол опережения, вписываем в таблицу угол отставания со знаком «минус»).
Таблица 1. Фазы рабочего цикла колеса с откидывающимися рычагами
| Фаза |
Углы точки отсчёта для фазы γ |
Угол опережения точки отсчёта α |
Расстояние до оси колеса |
| 1 |
271° .. 90° |
-76.0° |
82.5% |
| 2 |
91° .. 180° |
0° |
100.0% |
| 3 |
181° .. 270° |
формула (1.2) |
формула (1.1) |
Теперь смотрим полученные графики изменения текущего момента и суммарной нормированной работы для этой конструкции (в числах изменение моментов можно проследить по таблице пошагового изменения моментов).
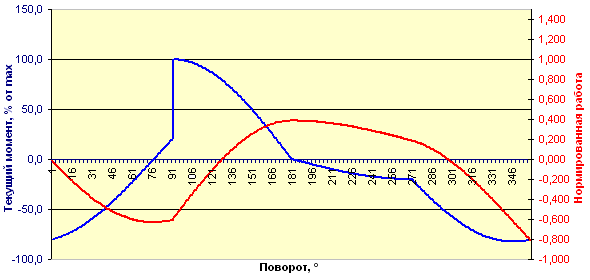 Текущий момент и суммарная нормированная работа одного элемента колеса с грузами на жёстких рычагах при соотношении r / R = 20%.
Нормированная работа за цикл от одного элемента: -0,807694.
Результат не просто отрицательный, а сильно отрицательный! Однако... Мы не учли, что в момент откидывания рычага груз падает на высоту этого рычага, и когда рычаг фиксируется в откинутом положении, его кинетическая энергия передаётся колесу — ведь больше деваться ей некуда (разве что на разрушение конструкции)! Конечно, такие удары не будут способствовать долговечности подобного колеса, однако сейчас мы оцениваем баланс энергии, а не разрушающие факторы. Итак, в этот момент груз падает на высоту рычага, т.е. в нашем случае — на 80% от базового плеча. Соответственно, в момент фиксации его кинетическая энергия должна быть равна высвободившейся потенциальной энергии, равной высоте (80%), умноженной на вес груза (100%), т.е. 0.8.
Складываем полученную нормированную работу с найденной добавкой энергии: –0.808 + 0.8 = -0.008. Результат становится близким к нулю, как и положено для замкнутой системы без учёта потерь, однако никакого положительного выигрыша, тем более существенно превышающего погрешности вычислений, нет и не предвидится...
Другие варианты, например, с ломаными рычагами, также не дают положительной прибавки энергии, лишь расчёт кинематики для них существенно сложнее.
Колесо с рычагами, складывающимися внутрь
Однако для изменения вращающего момента не обязательно откидавать рычаги наружу. Ведь на этапе обратного хода можно уменьшать момент, складывая рычаги внутрь и тем самым перемещая груз к ступице колеса.
В отличие от колеса д'Оннекура, в этом случае рычаги с грузами подвешиваются не снаружи, а внутри обода, и это коренным образом меняет дело.
Описание конструкции
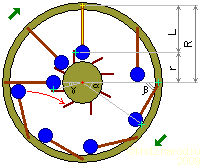 Колесо с грузами на складывающихся внутрь рычагах. R — плечо точки крепления рычага и положения груза на ободе, r — плечо груза в сложенном положении рычага, L — расстояние между точкой подвеса и центром масс груза (плечо рычага), α — угол опережения точки отсчёта лежащим на ободе грузом, β — угол отклонения рычага от нормального направления при лежащем на ободе грузе, γ — угол отставания места контакта груза с поддерживающей площадкой от точки отсчёта. Зелёные крестики отмечают точки приложения силы тяжести груза в различных фазах рабочего цикла. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта.
Здесь во время обратного хода после достижения вертикального положения рычага груз, до тех пор лежавший на внутренней поверхности обода, откидывается к ступице колеса. Чтобы он не проскочил обратно к ободу и не пришлось его поднимать вторично, на ступице предусмотрена соответствующая площадка, удерживающая груз в положении с наименьшим вращающим моментом на всё оставшееся время обратного хода. После достижения положения ВМТ груз полностью перестаёт давить на поддерживающую площадку и на этапе рабочего хода весь его вес через рычаг и подвес снова прикладывается к ободу колеса с максимальным вращающим моментом. Тем самым создаётся дисбаланс моментов, который должен вызвать вращение.
Кинематика грузов
Кинематика грузов здесь значительно сложнее, чем в случае колеса с рычагами, откидывающимися наружу. Достаточно сказать, что вес груза может передаваться на колесо в трёх точках: в месте подвеса рычага к ободу, в месте, где груз непосредственно лежит на ободе и в месте, где груз лежит на поддерживающей площадке возле ступицы. При этом угловое расстояние α между точкой подвеса рычага и точкой опоры лежащего груза на обод жёстко определяется соотношением радиуса обода и длины рычага:
α = 2 · arctg((L / 2) / R) = 2 · arctg((R – r) / (2 · R)) = 2 · arctg(0.5 – r / (2 · R)) (2.1)
где R — радиус колеса; L — плечо рычага, на котором подвешен груз (расстояние от точки подвеса рычага до центра масс груза); r — расстояние от оси колеса до точки контакта груза с ограничивающей площадкой, равное разности радиуса колеса и длины рычага.
В качестве точки отсчёта выберем точку подвеса рычага к ободу. В этом случае точка непосредственного контакта с колесом груза, лежащего на ободе, будет опережать точку отсчёта на угол α, а точка контакта груза с центральной поддерживающей площадкой — отставать от него на некоторый угол γ, зависящий от геометрии самого груза. В случае плоского груза γ → 0.
Теперь определим параметры фаз движения. Как всегда, считаем, что колесо движется очень медленно и влиянием центробежных сил пренебрегаем, потери на трение не учитываем, а все удары деталей друг о друга считаем неупругими.
При определении границ фаз имеем в виду, что рычаг с касающимся обода грузом приобретает вертикальное положение в моменты, когда точка отсчёта не доходит до положений 90° и 270° на угол, равный α / 2.
Фаза 1. Висящий груз
Начнём рассмотрение с положения ВМТ. В этом случае груз уже не давит на поддерживающую центральную площадку, и весь его вес приложен к точке подвеса рычага на ободе и направлен вертикально вниз. Фаза начинается в положении ВМТ и заканчивается, когда свободно висящий груз касается обода колеса, то есть когда точка отсчёта не дошла до 90° на α / 2. На протяжении этой фазы случае плечо воздействия груза равно R, а угол опережения — нулевым.
В этой фазе вся работа груза является «полезной» для наших целей.
Фаза 2. Лежащий груз
Следующая фаза продолжается всё время, пока груз касается обода колеса — от 90° — α / 2 до 270° — α / 2, когда рычаг приобретает отрицательный наклон, и груз «отваливается» от обода и падает на центральную площадку.
В этом случае груз опережает точку отсчёта на длину подвеса, то есть на угол α, а его плечо равно R. При этом воздействие его веса на обод происходит в двух местах — в точке непосредственного контакта, где груз лежит на ободе, и через рычаг в точке подвеса. В результате доля веса, приходящегося на каждую из этих точек, постоянно перераспределяется в зависимости от угла поворота колеса — в нижнем положении груза всё воздействие сосредоточено в точке непосредственного контакта, а в начале и конце фазы, когда положение рычага практически вертикальное, весь вес воздействует на обод именно в точке подвеса.
В зависимости от угла поворота, на место непосредственного контакта приходится доля веса
где φ — текущий угол поворота точки отсчёта.
На точку подвеса приходится оставшаяся доля веса
δП = 1 – δK = 1 – cos(φ + α) (2.3).
В этой фазе работа груза разгоняет колесо до тех пор, пока он не достигнет самого нижнего положения. Затем его работа становится «вредной», тормозящей нужное нам движение колеса. Особо хочу обратить внимание на завершающую часть этой фазы, когда груз поднимается выше того положения, куда он затем переместится при «складывании» рычага. Эта часть траектории тормозит движение сильнее всего.
Фаза 3. Груз в середине колеса
После того, как во время обратного хода при повороте до 270° — α / 2 рычаг «сложился» внутрь колеса и груз упал на поддерживающую площадку возле ступицы, масса груза может воздействовать на две точки — на эту площадку и через рычаг на обод колеса в точке подвеса. Однако составляющая веса, воздействующая на точку подвеса рычага, на протяжении всей этой фазы направлена строго к центру колеса (по нормали к ободу), то есть она не оказывает никакого воздействия на изменение вращающего момента.
При этом сама площадка отстаёт от точки отсчёта на угол γ, зависящий от геометрии груза — чем более плоский груз, тем меньше этот угол.
В этой фазе вся работа груза является тормозящей нужное нам движение, однако плечо достаточно мало, что позволяет надеяться на относительно небольшое тормозящее воздействие.
Расчёт работы
Объединим все данные в таблицы для разных плеч, на основе которых можно будет выполнить расчёт. Угол α здесь вычисляется по формуле (2.1), а φ — текущий угол поворота точки отсчёта.
Таблица 2.1. Фазы рабочего цикла колеса со складывающимися рычагами для плеча, равного радиусу колеса R
| Фаза |
Углы точки отсчёта для фазы |
Угол опережения точки отсчёта |
Масса груза для данного плеча |
| 1 |
1° .. 90° – α / 2 |
0° |
1 |
| 2 |
91° – α / 2 .. 270° – α / 2 |
α
0° |
cos(φ + α)
1 — cos(φ + α) |
| 3 |
270° – α / 2 .. 360° |
0° |
0 |
Таблица 2.2. Фазы рабочего цикла колеса со складывающимися рычагами для плеча, равного радиусу поддерживающей площадки r
| Фаза |
Углы точки отсчёта для фазы |
Угол опережения точки отсчёта |
Масса груза для данного плеча |
| 1 |
1° .. 90° – α / 2 |
γ |
0 |
| 2 |
91° – α / 2 .. 270° – α / 2 |
γ |
0 |
| 3 |
270° – α / 2 .. 360° |
γ |
sin(φ) |
Если принять четырёхкратное соотношение радиусов (r = 0.25 · R), то α = 41.1°. Приняв γ = 5°, и округлив α до 42° (углы смены фаз при этом будут 1°..69°, 70°..249° и 250°..360°), выполним расчёт.
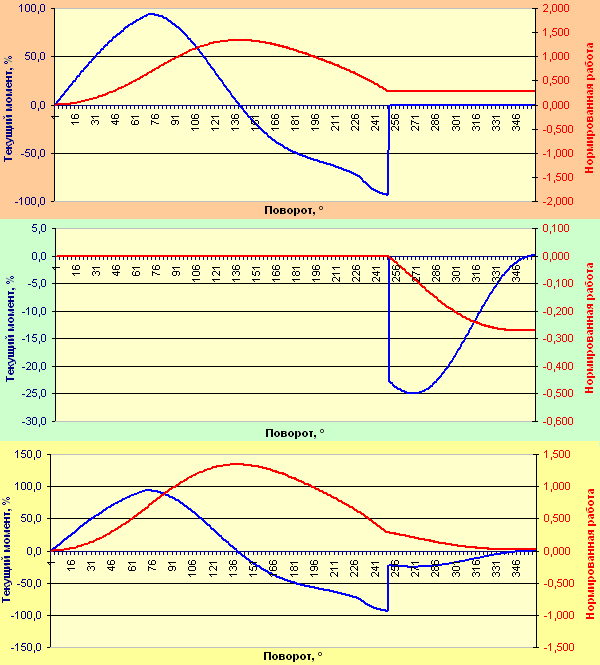 Текущий момент и суммарная нормированная работа одного элемента колеса с рычагами, складывающимися внутрь, при радиусе поддерживающей площадки 25% от радиуса обода и отставании сложенного груза на 5°.
Нормированная работа за цикл на ободе колеса от одного элемента (красный фон): 0,287539.
Нормированная работа за цикл одного элемента в сложенном состоянии (зелёный фон): 0,271448.
Суммарная нормированная работа за цикл одного элемента (жёлтый фон): 0,016091.
Суммарный результат получился небольшой, но положительный! Однако... При откидывании рычага груз падает на площадку и передаёт ей импульс, набранный во время падения. Этот импульс направлен против предполагаемого вращения колеса и, хотя плечо в точке удара мало, его достаточно, чтобы «съесть» весь небольшой выигрыш, полученный нами.
Можно попытаться удлинить рычаг, чтобы груз падал точно на ось или даже за неё, придавая колесу положительный импульс и выполняя в фазе 3 уже не «вредную» тормозящую работу, а «полезную» разгоняющую. Но с увеличением длины рычага сильно возрастает вклад «особо вредного» окончания фазы 2 (из-за большей длины рычага груз «отвалится» от обода позже) и сокращается «полезная» работа в двух первых фазах. Так что выигрыша и здесь получить не удаётся...
♦
|