Как конструировать механический вечный двигатель | Perpetuum mobile: «свободная энергия» и вечные двигатели.

При всём разнообразии конструкций различных колёс (реже — рычагов-коромысел) с перемещающимися грузами и резервуарами, претендующих на почётное звание «гравитационного вечного двигателя», главная идея почти всегда одна и та же — добиться разности моментов сил при рабочем и обратном ходе элементов, которая и должна вызвать вращение этого колеса или качание балансира. Для создания момента силы чаще всего используется сила тяжести или (реже, в погружных и полупогружных конструкциях) — выталкивающая сила Архимеда, она же сила плавучести. Все конструкторские ухищрения сводятся к игре с этими моментами и их комбинациями, призванными обеспечить превосходство «полезных» моментов над «вредными». Но поскольку суть одна, то при конструировании следует учитывать одни и те же аспекты, а для анализа работоспособности конструкции можно использовать универсальную методику, применимую практически к любому устройству класса «вечно вращающихся механических колёс» или «мельниц».

Эта страница посвящена обсуждению именно таких гравитационных колёс, хотя многое из изложенного здесь применимо и к другим типам устройств, предполагающих иные принципы получения «вечного движения», но имеющих механические узлы.

Минимум необходимых сведений по механике изложен в справочной информации и на специальной странице этого раздела. Однако их надо правильно применить. Кроме того, прежде чем брать в руки дрель и напильник, желательно просчитать работоспособность конструкции на бумаге или на компьютере — исписанный листок и пара часов на моделирование обычно несравнимы с затратами на изготовление конструкции в натуре (случаи, когда изобретатель воплощает своё детище в дереве и металле не столько в целях утилитарной проверки, сколько из эстетических соображений — не в счёт).

Момент сил и вращение колеса

Из правила моментов следует, что если мы возьмём рычаг, закреплённый на оси посередине, и обеспечим неравенство моментов сил на его сторонах, то он начнёт вращаться в сторону действия нескомпенсированного момента сил. В условиях гравитации для этого достаточно на одной стороне рычага разместить груз, а другую оставить пустой. Однако, как мы выяснили, рассматривая вращение рычага с грузом, если такой рычаг отпустить в положении с максимальной потенциальной энергией — положении верхней мёртвой точки (ВМТ), то максимум, на что хватит его энергии, так это только на то, чтобы вернуться обратно в эту точку. Любой отбор энергии, в том числе неизбежные в реальном мире потери на трение (или преодоление сопротивления среды) приведут к тому, что груз не сможет опять достичь ВМТ и вместо кругового движения мы получим колебания маятника, который рано или поздно остановится в нижней мёртвой точке (НМТ). Однако для того, чтобы движение было постоянным, нам необходимо в конце рабочего цикла вернуть груз точно в исходное положение.

При разных положениях относительно вертикали груз обеспечивает разный вращающий момент. Очевидно, что для максимальной эффективности следует поддерживать наибольшую разность моментов в положениях, близких к горизонтали, где вращающий момент максимален. А вот операции, связанные с изменениями моментов, лучше всего выполнять в положениях, близких к вертикали, когда вращающий момент мал и потери от его неэффективного использования, неизбежные при этой операции, минимальны.

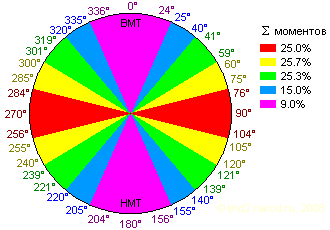Распределение весов моментов при вращении колеса.

Распределение весов вращающих моментов при вращении рычага с грузом вокруг шарнира. Цветами выделены зоны с различными весами моментов.

Из рисунка видно, что в жёлтой и красной зоне вращающий момент обеспечивает более половины полезной (или вредной) работы — в этих секторах следует обеспечить наилучшее соотношение моментов для рабочего и обратного ходов. Синие и фиолетовые секторы дают менее четверти общей работы за цикл, поэтому именно там надо стараться совершить все операции, связанные с изменением соотношения моментов между рабочим и обратным ходами элемента конструкции, тогда потери эффективности будут минимальны. В идеале хорошо бы уложиться в границы фиолетовых секторов, имеющих довольно большую протяжённость (50° в районе ВМТ и столько же в районе НМТ), в то время как работа, которую можно получить от гравитации в этих секторах, составляет менее 10% от общей работы за цикл!

Главное условие успешной работы «вечно вращающегося колеса»

Очевидно, что если бы удалось совершить бóльшую работу в рабочей части цикла (для сухопутного колеса — это вниз от ВМТ к НМТ) и обойтись меньшей при обратном ходе (вверх от НМТ к ВМТ), то мы добьёмся желаемого результата, да при этом ещё получим и некоторый избыток энергии, который сможем использовать в своих целях — вот и вожделенный вечный двигатель! Именно на это и направлены усилия конструкторов механических генераторов свободной энергии любой разновидности. Для колёс-«мельниц» в данном случае понятия момента и работы аналогичны (будет положительный момент — будет и положительный выход работы), но в более общем случае, конечно, следует говорить именно о работе. Естественно, в случае одного элемента при обратном ходе движение может сильно замедлиться, поскольку его кинетическая энергия тратится на возврат груза в исходное положение, в результате ось будет вращаться крайне неравномерно — то быстро, то медленно. Однако это легко исправить — достаточно добавить в конструкцию такое число элементов, смещённых друг от друга на некоторый угол, чтобы в каждый момент времени сумма разгоняющих моментов от элементов, совершающих рабочий ход, превышала сумму тормозящих моментов от элементов, совершающих обратный ход. Тогда вращающий момент всегда будет положительным и наше колесо станет вращаться равномерно (а в отсутствие сопротивления внешней среды и отбора энергии — с постоянным ускорением). И всё же непременное условие успешной работы — положительная суммарная работа за рабочий цикл каждого элемента конструкции. В случае механического колеса это сводится к условию положительного, т.е. направленного в сторону рабочего вращения, суммарного момента.

Если суммарный момент одного элемента за рабочий цикл получится отрицательным, то сколько бы элементов мы не включили в конструкцию, общий момент также будет отрицательным и такое колесо неизбежно остановится. Причём не надо обольщаться мыслью, что если этот момент отрицательный, то колесо начнёт крутиться в другую сторону — ничего подобного, в данном случае отрицательный суммарный момент означает именно работу против любого движения и является моментом торможения — прижмите к вращающемуся колесу тормозную колодку, и оно остановится независимо от того, в какую сторону вращалось!

Способы получения разности моментов

Способов получить разность моментов для гравитационных вечных двигателей не так уж много.

Во-первых, можно приложить внешнюю дополнительную силу. Однако в таком случае источник этой дополнительной силы находится вне нашего устройства. Этот вариант ещё можно допустить для вывода предполагаемого вечного двигателя на рабочий режим, однако постоянное использование его во время работы превращает наше колесо в самый обычный механизм с внешним приводом. Поэтому этот вариант отбрасываем.

Во-вторых, разность моментов можно получить, изменяя плечо между грузом и осью вращения при его постоянном весе — увеличивая на рабочем ходе и уменьшая на обратном. Пожалуй, это наиболее популярный способ у изобретателей, поскольку требует лишь перемещения груза, которое зачастую кажется организовать гораздо легче, чем изменение его веса.

В-третьих, для получения разности моментов можно изменять вес груза, не меняя его плечо. На самом деле это не так уж сложно — существует множество конструкций, где в разнообразные контейнеры что-то скатывается, насыпается или наливается в верхней части колеса и покидает их внизу. Тем не менее, для того, чтобы такой двигатель можно было назвать «вечным», он должен своими силами доставить отработанное рабочее тело на исходную позицию, а вот здесь-то и возникает очень большая проблема под названием «закон сохранения энергии». Новые возможности даёт использование конструкций, погружённых в воду — там вес (плавучесть) элементов можно менять, ничего не переливая и не пересыпая, а лишь изменяя их объём. Однако при этом приходится бороться с разностью давлений на глубине (где объём следует увеличить) и у поверхности (где объём следует уменьшить).

Наконец, в-четвёртых, можно одновременно менять вес и плечо груза. Теоретически это наиболее эффективно, однако на практике обычно значительно усложняет техническую реализацию конструкции.

Классы механических вечных двигателей

Классификация по используемым силам и окружающей среде

В механических вечных двигателях обычно используется только гравитация в двух её ипостасях — силы тяжести и силы Архимеда. Иногда в конструкциях задействуются и другие принципы, прежде всего инерция и сила упругости, однако, как правило, они применяются только для временной аккумуляции энергии и потому не могут рассматриваться как первичный источник энергии. Если в конструкции в тех же целях используются магнитные, электрические и прочие силы (именно и только для аккумуляции энергии с её последующим полным возвратом), то такую конструкцию также можно отнести к механическим вечным двигателям.

Конструкции, использующие только силу тяжести. Это наиболее обширный класс механических вечных двигателей, как правило использующий разность плеч, реже — разность весов в рабочем и обратном ходе. Практически все конструкции этого класса подразумевают работу в среде с малой плотностью — на воздухе или в вакууме, где сила тяжести проявляет своё действие в полном объёме, а малое сопротивление среды позволяет широко использовать инерцию. Рабочим ходом в таких конструкциях является движение рабочего тела (груза) вниз, обратным ходом — движение вверх, возвращающее его на исходную позицию. Однако по сути в таких конструкциях изобретатели пытаются заставить одну и ту же силу работать саму против себя. С точки зрения здравого смысла это занятие заведомо бессмысленно, что подтверждает многовековой опыт безуспешных попыток. Тем не менее, многие моменты в таких конструкциях проявляются наиболее наглядно, поэтому для анализа и обучения они самые удобные.

Конструкции, использующие только силу Архимеда. Здесь рабочие элементы имеют плотность меньше окружающей среды, и потому в свободном состоянии стремятся вверх. Обычно средой является вода. Устройства этого класса встречаются реже, и по сути являются зеркальным отражением предыдущего класса (рабочий ход вверх, обратный — вниз). Кроме того, высокая плотность окружающей среды обуславливает заведомо низкие скорости движения и практически не позволяет использовать инерцию как средство аккумуляции энергии. Конструкции этого класса могут быть как полностью погружёнными, так и погружёнными частично, когда часть рабочего цикла проходит в воздухе — среде с малой плотностью и в отсутствии силы Архимеда. В остальном все замечания, сделанные для предыдущего класса, верны и здесь.

Конструкции, использующие как силу тяжести, так и силу Архимеда. Выглядят наиболее перспективными, так как используют две встречно направленные силы. Также, как и в предыдущем классе, они могут быть погружены в жидкость полностью или частично, рабочий ход направлен вверх, а обратный — вниз. Как правило, в таких конструкциях рабочее движение происходит за счёт силы Архимеда (всплытия элемента), а сила тяжести используется для уменьшения плавучести элемента на обратном ходе за счёт уменьшения его объёма, реже — для изменения плеч. Однако и здесь, при более глубоком рассмотрении, обе силы являются производными гравитации. Камнем преткновения тут обычно является необходимость учитывать работу против разности давлений при изменении объёма элементов — на глубине, где объём элемента должен увеличиваться, но давление велико, и у поверхности, где объём (и плавучесть) элемента следует уменьшить, а давление жидкости мало.

Использование других принципов сразу переводит конструкцию в другой тип: разность температур — в тепловые машины, постоянных магнитов — в магнитные, кулоновских сил — в электростатические, переменных электромагнитных полей — в электромагнитные, эффектов высокоскоростного кругового движения (обычно газа или жидкости) — в вихревые.

Классификация по типу движения

По типу движения механические вечные двигатели (как впрочем, и двигатели других типов) можно разделить на использующие круговое или колебательное движение. Львиная доля конструкций ориентирована на круговое движение — оно обеспечивает наиболее удобную для использования форму механической энергии. Использование колебательного или возвратно-поступательного движения встречается гораздо реже, хотя здесь можно задействовать такие интересные возможности, как, например, резонанс.

В свою очередь, двигатели с круговым движением можно разделить на «колёсные» и «цепные». В первом случае всё вращается на одной единой оси, как у обыкновенного колеса. В «цепном» варианте имеются как минимум 2 шкива (ролика, звёздочки), разнесённых по высоте и соединённых между собой цепью с рабочими элементами (иногда вместо цепи могут использоваться ремни, конвейерные ленты и пр.). В этом случае наиболее выгодная фаза, соответствующая горизонтальному положению рабочих элементов при работе на «колесе», как бы растягивается по вертикали на расстояние между осями верхнего и нижнего шкивов с целью обеспечить прирост эффективности по сравнению с работой обычного колеса.

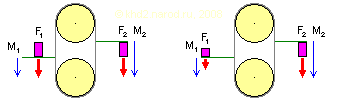«Цепной» вариант гравитационного вечного двигателя.

Моменты и силы на вертикальном участке цепного варианта механического вечного двигателя, использующего силу тяжести. Красным показан вес груза, синим — моменты, нормированные к концам рабочих элементов (рычагов).

Однако сразу следует подчеркнуть, что переделывать в «цепной» вариант можно только механизмы, использующие для создания разности моментов разность веса, а не разность плеч. На рисунке наглядно видно, что на вертикальном участке между осями шкивов рабочие элементы опираются, по сути, на две опоры, и полезный в колесе вращающий момент здесь превращается в бесполезный опрокидывающий, стремящийся наклонить всю конструкцию в целом и компенсируемый реакцией опор осей шкивов, — ведь вертикальные участки цепи должны лишь двигаться вверх или вниз, а не вращаться в вертикальной плоскости. Только разность сил на сторонах рабочего и обратного хода может вызвать движение цепи, в данном случае это — разность веса рабочих элементов. В левом варианте, несмотря на различие моментов, силы тяжести от грузов, действующие на цепь справа и слева, одинаковы, поэтому суммарный вращающий момент от этих сил равен нулю. В правом варианте силы различны, и потому их разность способствует движению цепи в направлении действия большей силы.

Классификация по типу рабочего тела (груза)

Когда груз жёстко прикреплён к элементам конструкции, его тип не имеет значения — это с одинаковым успехом может быть и банка с водой, и мешок с песком, и кирпич, и металлический шар. Однако в тех случаях, когда груз должен перемещаться сам по себе, обычно используются всего два базовых способа такого перемещения — перетекание жидкостей или перекатывание твёрдых шаров.

В самом первом «вечновращающемся колесе», о котором упоминается в письменных источниках, в качестве рабочего тела (перемещающегося груза) предлагалось использовать жидкость — воду или, для большей эффективности, ртуть. С тех пор в конструкциях, где рабочее тело должно было перемещаться «само по себе», без помощи механических рычагов, изобретатели практически всегда предполагали использовать ту или иную жидкость, что было очень удобно — достаточно изменить наклон дна сосуда, и она сама перетечёт в нужную сторону. Однако в результате развития технологии — прежде всего точной обработки твёрдых материалов — конструкторы всё чаще стали заменять жидкость твёрдыми шарами, обычно каменными или металлическими. Основных причин для этого две.

Во-первых, трение твёрдого шара, свободно катящегося по гладкой твёрдой поверхности, очень мало и может быть даже меньше потерь энергии при перетекании жидкости. При этом отпадает необходимость в герметизации конструкции, — она сразу упрощается и облегчается, — а также нет необходимости использовать такое тяжёлое, но ядовитое и достаточно редкое вещество, как жидкая ртуть. Вода же по сравнению с металлическими шарами не эффективна из-за своей малой удельной плотности. Главное условие здесь — и форма шара, и ровность поверхности направляющих должны быть близки к идеальным. Именно поэтому широкое использование шаров получило распространение лишь тогда, когда достаточно высокая точность обработки перестала быть слишком трудоёмким и долгим процессом.

Во-вторых, при перетекании жидкости её поверхность всегда горизонтальна, поэтому, пока дно сосуда (направляющая) имеет небольшой наклон, вся жидкость не сможет собраться в нижнем конце из-за слишком малой разности уровней дна. По этой причине верхний конец сосуда освободится только тогда, когда центр масс жидкости будет ниже его уровня (причём существенно ниже), так как необходимо дождаться, когда наклон станет достаточно большим, чтобы вся жидкость смогла собраться внизу, — а это потеря эффективности. Для шара же достаточно минимального наклона — и он весь начнёт перемещаться вниз, даже если его центр тяжести продолжает оставаться намного выше уровня верхнего края направляющей! В результате при использовании шаров центр масс груза может перемещаться в нужном направлении гораздо раньше и быстрее, чем при перетекании жидкости — а это повышает эффективность.

Поэтому в современных конструкциях вместо перетекающих жидкостей обычно используются перекатывающиеся шары (к тому же рассчитать конструкцию с шарами гораздо проще, чем конструкцию с постепенно перетекающей жидкостью). Исключение составляют лишь те системы, где задействован не один лишь вес жидкости, а используются её гидростатические и гидродинамические свойства, которые шары в принципе обеспечить не могут.

Как рассчитать работоспособность

Как уже говорилось выше, главным условием успешной работы является суммарная положительная работа каждого элемента конструкции за полный рабочий цикл. Особо подчеркну ещё раз — именно за ПОЛНЫЙ РАБОЧИЙ ЦИКЛ, когда рабочий элемент возвращается точно в исходное положение, поскольку иногда всё остальное может давать заметный выигрыш, но «последний дюйм» пути к исходному положению съедает всё! Таким образом, для оценки работоспособности вновь изобретённой конструкции достаточно оценить только этот параметр.

Для наиболее распространённого случая колеса расчёт суммарной работы эквивалентен расчёту суммарного момента. Этот наиболее частый случай мы и рассмотрим подробнее.

Что необходимо учесть при оценке работоспособности

Для предварительной оценки работоспособности тихоходного гравитационного «вечного двигателя» необходимо учесть не так уж много факторов, а точнее — всего три. Во-первых, это изменение массы груза. Впрочем, если разность моментов создаётся только за счёт изменения плеча, этот фактор можно не учитывать. Вторым необходимым фактором является расстояние от центра груза до оси вращения, т.е. его перемещение по нормали (плечо). И, наконец, третьим важнейшим фактором является учёт тангенциального смещения груза, нормированного к углу поворота — то есть насколько в данный момент центр масс груза обгоняет выбранную фиксированную точку на ступице колеса или отстаёт от неё. Этот фактор очень часто упускают из вида, считая, что его влияние на баланс моментов весьма мало, и им можно пренебречь. На самом деле это влияние ОЧЕНЬ ЗНАЧИТЕЛЬНО! Расчёты показывают, что зачастую именно этот фактор обуславливает неработоспособность конструкции, а изменение положения груза на 15° вперёд или назад легко способно «съесть» весь выигрыш от двукратного изменения плеча!

В случае погружных конструкций с изменяющими объём элементами обязательно надо учесть и четвёртое условие — точно просчитать работу, которую необходимо совершить против давления среды при увеличении объёма элемента на глубине (которая может быть частично компенсирована работой, полученной при уменьшении объёма у поверхности). Очень часто этот фактор прикидывают «на глазок» и сильно недооценивают его влияние. Между тем, точный расчёт обычно даёт цифры, не оставляющие никаких шансов на длительную самостоятельную работу очередного шедевра технической мысли.

Если предполагается использование не только гравитационной, но и других сил, скажем магнитной или электростатической, необходимо учитывать их влияние на всей траектории движения рабочего элемента, в том числе и во время обратного хода! При этом, в отличие от гравитации, которую в пределах нескольких десятков метров у земной поверхности можно считать однородной и неизменной, эти силы обычно носят выраженный центральный характер и при небольшом расстоянии до источника их нельзя считать однородными ни по величине, ни по направлению. Если предполагается модуляция таких сил какими-либо экранами или другими объектами (скажем, встречным магнитным полем или зарядом противоположного знака), необходимо учитывать получающиеся при этом искажения распределения в пространстве соответствующих полей, а в случае динамического управления такими модуляторами — нельзя пренебрегать и затратами работы на их включение-выключение или механическое перемещение в этих полях.

Наконец, если речь идёт о конструкциях с принудительным стартом, которые предварительно необходимо разогнать до определённой скорости, очень часто (хотя и не всегда!) нужно учитывать инерцию движущихся деталей и узлов, в том числе и центробежные силы.

Все эти факторы необходимо учитывать полностью и точно во всём рабочем цикле, даже если их влияние кажется «пренебрежимо малым» вообще или (особенно коварно!) на отдельных участках цикла. На самом деле пренебрежение любым из них, даже самым малозначимым, может дать ложные и необоснованные надежды на успех, которые практика всё равно развеет рано или поздно!

Чем можно пренебречь при оценке работоспособности

А вот практически всеми остальными факторами при первичной оценке работоспособности можно пренебречь. К ним относится трение во всех узлах конструкции (при достаточно больших размерах его практически всегда можно считать пренебрежимо малым), сопротивление среды (и жидкая, и газообразная среда на малых скоростях сопротивляются движению не слишком сильно, а ведь прежде всего нам надо, чтобы конструкция принципиально пришла в движение). Также можно не учитывать деформации и вес всех частей конструкции помимо рабочего тела (груза).

Конечно, если, паче чаяния, конструкция окажется работоспособной, для получения максимальной эффективности всё это придётся принять во внимание, однако сначала надо пройти первый этап — получить принципиально работоспособный механический «вечный двигатель».

Кроме того, довольно часто в первом приближении можно считать, что груз не обладает инерцией и при смене фазы работы перемещается из одного положения в другое (либо меняет свою массу) мгновенно. Для многих конструкций это тоже повышает расчётную эффективность, однако обычно и это допущение не спасает положения. В реальной же жизни инерция делает все изменения гораздо более длительными, «размывая» переходы между фазами работы. Центробежными силами, существенными при больших скоростях вращения, для малых скоростей часто тоже можно пренебречь. Но есть класс чисто механических конструкций «вечных двигателей», где инерция груза имеет принципиальное значение. Безусловно, там этим фактором пренебрегать ни в коем случае нельзя! В частности, к подобным механизмам относится одна из версий устройства знаменитого колеса Орфериуса. То же относится и к центробежным силам (как известно, являющимся одним из проявлений инерции) для конструкций, где именно они предполагаются в качестве необходимого условия работы установки.

Как рассчитать работоспособность

Алгоритм работы очень прост: выбираем на ступице колеса (или его неподвижном относительно ступицы ободе, если он предусмотрен конструкцией) некую точку. Это будет точка отсчёта. Часто в качестве начальной точки отсчёта удобно использовать верхнюю мёртвую точку рабочего элемента. Далее начинаем равномерно поворачивать точку отсчёта с небольшим шагом (я обычно использую шаг в 1°), и для каждого её положения вычисляем геометрическое положение груза (а если может меняться его масса — то и массу), определяем плечо и рассчитываем вращающий момент сил. Так делаем до тех пор, пока точка отсчёта не вернётся в исходное положение (в случае шага в 1° это будет 360 шагов). Затем суммируем все моменты и смотрим на результат — если он больше 0 (и больше погрешности вычислений), то конструкция в принципе рабочая, а если меньше — работать не будет ни при каких условиях.

Ещё раз подчеркну, что на выбранный шаг перемещается именно точка отсчёта, а не центр масс груза! Как раз груз в зависимости от кинематики может на разных фазах рабочего цикла как опережать точку отсчёта, так и отставать от неё. Углы отставания и опережения, а также перемещение центра масс от оси вращения необходимо вычислять точно, и здесь не обойтись без решения треугольников! Однако обычно в течение рабочего цикла элемент проходит не так много фаз, а внутри фазы эти параметры не меняются, так что редко когда приходится рассчитывать более четырёх положений. Любой другой подход будет ошибочным и приведёт к неверным результатам — прежде всего это относится к попыткам упростить расчёты и прикинуть параметры на глазок.

Итак, теперь можно начинать расчёт. Благодаря компьютеру нет необходимости расчерчивать лист бумаги на 360 строк, — ведь есть такой замечательный инструмент, как электронные таблицы, самой распространённой из которых является Microsoft Excel или её аналог из свободного пакета офисных программ OpenOffice — Calc (не путать с калькулятором Windows)! Какие графы должны быть в таблице?

Упакованный файл с таблицей можно скачать отсюда (187 237 байт).

Однако результат этой таблицы ещё не является окончательным вердиктом, поскольку иногда возникает необходимость учесть дополнительные затраты энергии, не учитываемые при расчёте моментов — например, работу по раскрытию-закрытию поплавков переменного объёма или затраты энергии на вспомогательное вертикальное перемещение грузов.

Нормированная работа за цикл и мощность

Как уже говорилось выше, суммарный момент, получающийся при расчёте по изложенной методике — понятие относительное, в частности, его абсолютная величина (но не знак!) зависит от выбранного шага точки отсчёта при численном моделировании. Поэтому использовать его для количественной оценки получаемой (или затрачиваемой) энергии не всегда удобно. Но если его отнормировать к числу шагов, то результат уже не будет зависеть от размера шага, а если ещё и разделить на длину окружности, то полученное число будет иметь абсолютно однозначный физический смысл — это работа, которую в данной конструкции производит или потребляет груз с единичным весом на рычаге единичой длины. Это и есть нормированная работа. Для системы СИ радиусу в 100% соответствует 1 м, а весу в 100% — 1 Н (т.е. вес в воздухе груза массой около 0.102 кг). Умножив нормированную работу на реальные значения выбранного радиуса и веса груза (в метрах и ньютонах), можно получить реальную отдачу или затраты энергии в джоулях (за цикл или за часть цикла). Разделив эту нормированную работу одного элемента за полный цикл на время одного оборота (в секундах), получим мощность, которую может дать один элемент. Умножив теперь это значение на общее число элементов, получаем полную полезную мощность конструкции при заданных размерах и массах грузов.

Однако польза нормированной работы не только в этом. Без неё не обойтись при расчёте «цепных» конструкций, а также погружных конструкций с изменямым объёмом поплавков, где надо учесть работу против давления жидкости.

Погрешности численных методов

Описанный метод расчёта является одним из вариантов численных методов моделирования с дискретным шагом. Возникающие при этом погрешности и достоверность результатов — отдельная большая тема, по которой написано немало диссертаций и монографий, но в данном случае нам наиболее важны два момента, которые могут привести к ложным выводам.

Во-первых, это погрешности из-за конечной точности представления чисел в компьютере. Впрочем, здесь используется не так уж много шагов, чтобы эти ошибки успели накопиться до сколько-нибудь существенной величины, и вряд ли они превысят миллиардные доли результата.

Во-вторых, это погрешности из-за дискретности шага отсчётов. По сути, вместо непрерывного «гладкого» вращения колеса мы выхватываем отдельные моменты этого движения, т.е. при моделировании колесо как бы «движется скачками». Из-за этого возможны довольно существенные ошибки, которые при 360 шагах иногда даже могут приближаться к 1%. Поэтому не следует обольщаться, если результат будет чуть-чуть положительный — скорее всего, это как раз тот самый случай!

Как же узнать, является ли полученный положительный результат истинным или ложным? Во-первых, можно увеличить или уменьшить шаг расчёта (скажем, выполнить расчёт для 90 шагов по 4° или для 720 шагов по 0.5°). Если выигрыш был ложным, то обычно он увеличивается при загрублении и уменьшается при использовании более мелкого шага примерно пропорционально изменению шага. Во-вторых, можно чуть сдвинуть начало фаз — на градус вперёд или назад. Результат изменится в любом случае, однако при этом реальный выигрыш должен всё равно остаться положительным, а если при столь малом повороте он вдруг стал отрицательным — это однозначно говорит о том, что положительный результат был получен лишь из-за погрешности вычислений!

Конечно, более правильно было бы описать функцию движения груза и затем проинтегрировать её за весь цикл, что соответствовало бы плавному вращению колеса. Однако это зачастую весьма трудоёмко, — по сравнению с этим численное моделирование по дискретным «маленьким шагам» гораздо быстрее и нагляднее, особенно для тех, кто с высшей математикой на «Вы». Кроме того, здесь в один приём мы можем не только получить конечный результат, но и проследить за поведением конструкции во время рабочего цикла — при интегрировании во многих случаях пришлось бы каждый раз брать интеграл до нужного угла поворота заново...

Наконец, следует отметить, что даже «честный» выигрыш менее 1% вряд ли способен принести реальную пользу: ведь мы не учитывали трение, сопротивление среды и прочие «мелкие пакости», а они вполне способны «съесть» столь малую полезную работу без остатка!

Расчёт конструкций, использующих несколько сил

К таким конструкциям относятся, во-первых, конструкции, в которых рабочий элемент имеет 2 и более грузов с различной кинематикой (траектории или время перемещения), а во-вторых, конструкции, использующие несколько сил (например, силу тяжести и силу Архимеда).

В любом случае, алгоритм одинаков — по каждому из грузов считаем свои моменты, а затем суммируем. В случае силы Архимеда поплавок рассматривается как самостоятельный груз с отрицательным весом (так и записываем с минусом, ведь он стремится вверх!). Единственное, о чём следует помнить: однажды выбрав точку отсчёта, единичный радиус и единичный вес, при расчёте всего устройства все силы, расстояния и перемещения следует нормировать именно к ним, а не использовать для каждого момента свои базовые параметры!

Расчёт конструкций с цепью элементов

Для расчёта «цепных» конструкций необходимо сначала «урезать» их до «колеса» и рассчитать нормированную работу для этого варианта. Затем необходимо определить баланс сил (именно сил, а не моментов!) для горизонтального положения колеса (положительный, если он вращает в нужную нам сторону, и отрицательный — если тормозит вращение). Теперь осталось умножить эту результирующюю силу на предполагаемое число рабочих элементов, которые будут находится между осями верхнего и нижнего шкивов, и на 2·π (длину окружности), а потом прибавить ее к нормированной работе, полученной при расчёте варианта, урезанного до колеса. Это будет нормированная работа всей конструкции за 1 оборот шкива (предполагается, что верхний и нижний шкивы имеют одинаковый диаметр). Чтобы узнать нормированную работу за 1 оборот цепи, надо умножить нормированную работу за 1 оборот шкива на отношение общей длины цепи (ремня, ленты) к удвоенной длине окружности шкива.

Когда верхний и нижний шкивы «цепной» конструкции имеют разные диаметры, при расчёте верхней (от 270° до 90°) и нижней (от 90° до 270°) частей колеса необходимо учитывать эту разницу для определения текущего плеча (радиуса) и угла отставания / опережения центром масс груза точки отсчёта.

Учёт работы против давления в поплавках с изменямым объёмом

Как уже отмечалось выше, в конструкциях с изменямым объёмом поплавков ни в коем случае нельзя пренебрегать учётом давления жидкости на подвижные части поплавка (обычно мембраны или поршни). Например, для площади размером всего 10х10 сантиметров при перепаде глубин в 10 метров разность давления воды будет равна весу груза массой 100 кг, на разнице глубин в 1 метр — 10 кг, и даже при изменении глубины всего на 10 сантиметров для преодоления разницы давления на такую площадь понадобится вес груза в целый килограмм! Поэтому так важно просчитать, сможет ли раскрыться (или закрыться) поплавок на запланированной глубине.

Хотя на практике в небольших конструкциях обычно лучше использовать мембраны, не имеющие, в отличие от поршней, потерь на трение, для оценки работоспособности более удобно рассматривать как раз поршни из-за более лёгкого расчёта изменений объёма. При этом в первом приближении вполне можно предположить трение поршня пренебрежимо малым.

Работу против давления жидкости можно несколько уменьшить, увеличив давление внутри поплавка (например, предварительно накачав его воздухом). Однако, выигрывая за счёт избыточного давления в работе при раскрытии поплавка на глубине, мы проиграем в работе, необходимой для закрытия поплавка у поверхности — теперь там придётся работать против избыточного внутреннего давления. А поскольку цикл движения поплавка у нас предполагается замкнутым (иначе это не будет вечный двигатель), в конце концов всё равно придётся преодолевать одну и ту же разность давлений. Поэтому для удобства можно посчитать, что в момент закрытия давление внутри поплавка равно давлению окружающей его среды, и эта операция даётся нам «даром», а вот для раскрытия поплавка на глубине необходимо приложить усилия и совершить дополнительную работу.

Оценить работу против давления можно несколькими методами.

Второй метод более предпочтителен, поскольку позволяет оценить реальность конструкции без выполнения относительно трудоёмкого расчёта моментов. Кроме того, анализ кинематики всё равно нужен для определения ходов поршня и груза, которые необходимо учитывать при расчёте моментов.

На что нельзя закладываться при конструировании механических вечных двигателей

Во-первых, из формулы, описывающей потенциальную энергию тела в гравитационном поле, следует, что разность энергий, а следовательно и работа, которая может быть получена или затрачена при этом перемещении, зависит только от разности высот начала и конца движения, но никак не от траектории движения между ними (естественно, при условии, что на тело действует только сила гравитационного поля). Поэтому устройство участков с разными углами наклона, в том числе волнообразного пути, не даст никакого выигрыша в энергии. Наоборот, более длинный путь приведёт лишь к увеличению потерь на трение, аэро- или гидродинамическое сопротивление. Впрочем, стоит отметить, что тщательно подобранный волнообразный профиль пути при определённых условиях может немного сократить потери на трение по сравнению с прямолинейным движением, однако не более того — за счёт лишь одной механики прирост энергии таким способом не получить.

Во-вторых, из закона сохранения импульса следует, что вариант, когда планируется сначала «медленно накопить» энергию, а потом её «быстро выпустить» и таким скачком преодолеть «мёртвую точку», не пройдёт — насколько рабочий элемент продвинется вперёд при скачке, настолько же он до того отойдёт назад при его подготовке. Отсылка к инерцоидам здесь не убедительна — они движутся в определённом направлении из-за разности сил трения или сопротивления среды при малых и больших скоростях, что наиболее просто доказывается противоположными направлениями их движения на суше и на воде. А силы трения всегда лишь «пожирают» энергию, которая нам так нужна — все инерцоиды имеют двигатели и большие затраты энергии на единицу пройденного пути. Тем не менее, оговорюсь, что некоторые создатели инерцоидов утверждают, что сочетание скорости и ускорения влияет на инерционную массу и может быть весьма важным...

В-третьих, работа не зависит от времени, и при оценке работоспособности конструкции понятиями «быстро» и «медленно» можно пренебречь — их вполне заменяют понятия «кинетическая и потенциальная энергия». Поэтому не следует закладываться на долгое сохранение «хороших» сочетаний моментов и быстрое прохождение их «плохих» комбинаций. Во многом эти попытки являются тем же самым, о чём говорилось в предыдущем пункте, только представлены с другой стороны! От времени зависит лишь мощность, но не она определяет принципиальную работоспособность конструкции. Впрочем, здесь есть одна оговорка. При быстром вращении могут возникать значительные центробежные силы, которыми нельзя будет пренебречь, поскольку они могут существенно изменять траекторию движению грузов.

В-четвёртых, из правила рычага следует, что рычаг может дать выигрыш в силе или в перемещении, но не в работе, которая, как известно, вычисляется как произведение этих величин. Поэтому всевозможные рычаги могут рассматриваться лишь как вспомогательные «трансформаторы силы», но невозможно получить выигрыш в энергии, построив конструкцию лишь на одних рычагах.

В-пятых, всевозможные резонансы позволяют лишь накопить энергию или сократить её непроизводительные потери, однако отдать энергии больше, чем предварительно было «накачано» в резонирующую конструкцию, они не могут в принципе. Тем не менее, это не значит, что резонанс вообще бесполезен. Иногда задержка во времени между получением и отдачей энергии в колебательном процессе, которым, по сути, является любой резонанс, может оказаться принципиально важной. Кроме того, резонанс помогает накопить и сконцентрировать энергию, необходимую для проявления эффектов различной природы, но это уже выходит за рамки чистой механики...

Наконец, в-шестых, в погружных конструкциях не стоит надеяться, что плавучесть несимметричного поплавка изменится, если он просто повернётся на другую сторону. В формуле закона Архимеда фигурирует только объём тела, но не его форма. Странно, довольно многие питают иллюзии на этот счёт, — а ведь из этого однозначно следует, что если тот же самый поплавок вытащить на сушу, то его вес можно было бы менять в зависимости от того, на какую грань его положить! Кроме того, не надо забывать, что сам по себе эффект Архимеда является лишь своеобразным отражением других сил, и потому в принципе не может дать дополнительной работы и энергии!

Использование данной методики расчёта для других типов двигателей

Эта методика применима ко всем типам двигателей, использующих достаточно медленное механическое круговое движение с дискретными рабочими элементами. Разница только в том, что там силы, вызывающие вращающий момент, могут иметь магнитную, кулоновскую или какую-либо другую природу, и точный расчёт их может оказаться весьма затруднительным. В самом деле, например, при взаимодействии постоянных магнитов сила их взаимного притяжения или отталкивания зависит от формы и взаимного положения полюсов в каждый момент времени, а также от расстояния между ними, резко возрастая при их сближении. При использовании электромагнитов, сила зависит не только от параметров их обмотки и сердечника, но и от рабочего тока в каждый момент времени, когда к электромагниту приближается или удаляется ферромагнетик или постоянный магнит (и, конечно, от расстояния между ними). Поэтому расчёт таких сил значительно более трудоёмок по сравнению с простым расчётом веса в однородном гравитационном поле.

Данная методика принципиально неприменима ко многим гидродинамическим и вихревым процессам — там на первую роль выходят другие эффекты, в частности, вызванные центробежными силами, а понятие дискретных рабочих элементов обычно отсутствует вообще либо они имеют вспомогательный характер (как, например, лопатки турбин).

О пользе уроков труда

И всё же, теория — теорией, но я знаю многих людей, для которых гораздо понятнее и убедительнее будет в течение нескольких минут потрогать в натуре и покрутить руками какое-нибудь устройство, чем прочитать о нём толстую книгу. Можно ли сделать такую модель заинтересовавшей Вас конструкции быстро и без больших необратимых затрат? Довольно часто — да!

Многие, хотя и не все, модели механических «вечных двигателей» можно изготовить в течение нескольких минут из детского механического конструктора — такие металлические конструкторы используются в начальной школе на уроках труда. Их детали обычно обладают вполне достаточной прочностью и неплохой точностью изготовления для того, чтобы можно было сделать опытную модель и проверить её принципиальную работоспособность. Возможно, одного конструктора будет мало, и придётся приобрести несколько наборов, в том числе и с разными комплектами деталей (главное, чтобы они были совместимы по размеру крепежа и шагу между отверстиями). Возможно, кое-что придётся добирать отдельно — например, магниты можно взять из магнитных защёлок для мебели (эти защёлки продаются в почти любом хозяйственном отделе по цене несколько рублей за штуку), большие стальные шарики — поискать в автомобильных мастерских и гаражах (прежде всего в подшипниках коробок передач). Но это всё равно быстрее и дешевле, чем сразу делать «серьёзную» модель своими руками «с нуля» и тем более заказывать её на заводе. И конечно, модель из конструктора можно быстро разобрать и использовать детали для следующих конструкций, что не всегда возможно с громоздкими «заказными» изделиями. ♦