Колёса с перекатывающимися шарами
Уже первые изобретатели «вечновращающихся колёс» обратили внимание на замечательное свойство жидкостей — достаточно придать дну сосуда хоть небольшой уклон, и жидкость сама перетекала в более низкую часть, собираясь там и увеличивая её вес. Это было очень удобно, и уже первая известная модель «вечного двигателя» использует это свойство жидкостей.
Однако по мере развития науки и технологии выяснилось, что во многих случаях гораздо эффективнее вместо жидкостей использовать твёрдые шары, перекатывающиеся по жёстким направляющим. В результате все колёса с переливающимися жидкостями рано или поздно получили аналоги с перекатывающимися шарами (не путать с системами, где жидкость не переливается внутри колеса, а льётся по колесу, а потом возвращается обратно другим путём). Для нас же рабочие элементы с перекатывающимися шарами интересны тем, что расчёт моментов для них выполнить гораздо проще и нагляднее, чем для перетекающей жидкости — применение принципа мгновенной смены фаз здесь очень близко к реальному поведению шаров на малых скоростях вращения колеса.
Колесо Бхаскары и колесо с шарами в наклонных спицах
Колесо со скошенными ящиками
Колесо с качающейся направляющей
Резюме
Колесо Бхаскары и колесо с шарами в наклонных спицах
Первое упоминание в письменных источниках о «вечновращающемся колесе» относится к XII веку. Оно описано индийским поэтом, математиком и астрономом Бхаскарой Ачарья. В этом колесе наклонные полые спицы предлагалось заполнить ртутью наполовину. В первой фазе рабочего хода спица, находясь ещё значительно выше оси колеса, постепенно принимала горизонтальное положение и ртуть перетекала от центра колеса к его ободу, увеличивая вращающий момент. В первой фазе обратного хода та же спица, ещё находясь намного ниже оси колеса, начинала переворачиваться обратно, и ртуть снова возвращалась к центру колеса, уменьшая вращающий момент. Таким образом, на участке между горизонтальными положениями оси предполагалось наличие положительного вращающего момента, а на остальных участках моменты рабочего и обратного хода должны были взаимно компенсироваться, что позволило бы обеспечить суммарный положительный момент за полный цикл рабочего элемента.
Расчётов, естественно, автор не проводил — компьютеров тогда не было, да и механики как точной науки тоже. О воплощении колеса в натуре сведений также не сохранилось, а работоспособность обосновывалась просто — оно будет вращаться, потому что это очевидно!
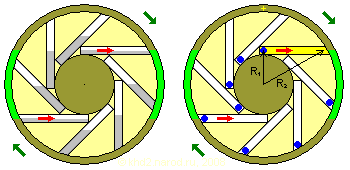 Слева — колесо Бхаскары (Индия, ок.1150 г.), справа — его аналог с перекатывающимися шарами. Предполагаемая область положительного вращающего момента показана на ободе зелёным цветом. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта.
Но сейчас компьютеры есть, поэтому расчёт такой конструкции много времени не займёт. Глядя на аналог с шарами, можно заметить, что фаз всего две. При переходе в рабочее положение груз перемещается к ободу с радиуса R1 на радиус R2 и несколько опережает точку отсчёта, а в начале обратного хода возвращается на меньший радиус и вновь начинает вращаться синхронно с точкой отсчёта. Следует подчеркнуть, что R1 и R2 — это не радиусы ступицы и обода, а расстояние от оси колеса до центра масс груза при обратном и рабочем ходе соответственно.
Трение, сопротивление среды и прочее в первом приближении можно не учитывать. Масса груза в данном случае не изменяется. Для упрощения расчёта выберем точку отсчёта таким образом, чтобы в фазе обратного хода её угол поворота был равен углу поворота центра масс груза, и предположим тангенциальное размещение спиц по отношению к ступице. В этом случае, как видно из рисунка, R1 и R2 образуют прямоугольный треугольник, где R2 является гипотенузой, а R1— катетом. Для расчёта нам не хватает только угла опережения точки отсчёта во время рабочего хода, который как раз равен углу между R1 и R2 на рисунке.
Из решения треугольников следует, что длина катета равна длине гипотенузы, умноженной на косинус угла между ними, соответственно угол равен β = arccos(R1 / R2). Теперь можно выполнить расчёт для нескольких соотношений R1 и R2 в предположении, что перемещение груза длится один шаг после горизонтального положения спицы — рабочий ход начинается при повороте точки отсчёта на 1°, а обратный — начиная со 181°.
| Отношение R1 / R2 |
Угол опережения β |
Угол наклона спицы к радиусу колеса |
Нормированная работа за цикл |
| 5% |
87.1° |
2.9° |
-0,016245 |
| 25% |
75.5° |
14.5° |
-0,016137 |
| 50% |
60.0° |
30.0° |
-0,015115 |
| 75% |
41.4° |
48.6° |
-0,011320 |
| 95% |
18.2° |
71.8° |
-0,005507 |
Итак, при всех углах наклона спиц суммарная нормированная работа отрицательна, а это значит, что данная конструкция принципиально неработоспособна! При этом чем ближе положение спицы к нормальному (т.е. совпадающему с радиусом колеса), тем меньше потери. Сразу скажу, это потому, что мы предположили конечное время перехода груза из положения обратного хода в положение рабочего хода, равное времени поворота на один градус (R = R2 начиная с 1° и R = R1 начиная со 181°). Если мы предположим абсолютно мгновенное перемещение груза (R = R2 начиная с 0° и R = R1 начиная со 180°, а главное, также чуть раньше менялся бы и угол опережения), зависимость будет обратной, но всё равно все значения будут отрицательными, а если вдруг окажутся чуть-чуть положительными, то лишь из-за особенностей численных методов моделирования — желающие могут проверить самостоятельно, это несложно, — достаточно уменьшить шаг (скажем, до 0.1°, 3600 шагов) и сразу же пропорционально уменьшится мнимый выигрыш!
И всё-таки, почему так получилось? Чтобы ответить на этот вопрос, необходимо проанализировать изменение текущего и суммарного моментов, например, для соотношения радиусов 50%.
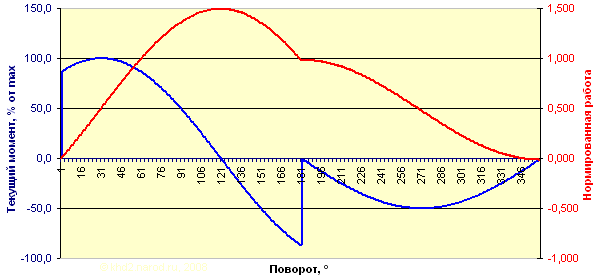 Текущий момент и суммарная нормированная работа одного элемента колеса Бхаскары при соотношении R 1 / R 2= 50%.
Нормированная работа за цикл от одного элемента: -0,015115.
На графиках наглядно видно, что когда груз находится в рабочем положении (возле обода), он успевает «отъесть» значительную часть полезной работы, прежде чем вернётся к ступице. В то же время, возвратившись к ступице, он «отматывает» назад и свой угол поворота, и если в рабочем положении, длящемся половину оборота колеса, он совершал как «полезную», так и «вредную» работу, то вторую половину оборота при обратном ходе он совершает только «вредную» работу, хотя и меньшую — из-за уменьшившегося момента, — но этого достаточно, чтобы «доесть» остатки полезной работы от первой половины оборота.
Как с этим бороться? Во-первых, можно попытаться увеличить разность плеч рабочего и обратного ходов, то есть разность между R1 и R2. Однако при этом наклон спицы относительно радиуса уменьшается, и сокращается сектор, где предполагается получить положительную разность моментов, — достаточно взглянуть на рисунок колеса. В результате выигрыша нет, и расчёты это подтверждают. Второй путь — максимально расширить сектор с положительной разностью моментов. Однако при этом разница между R1 и R2 сокращается (таковы законы геометрии в нашем мире!), и, соответственно, уменьшается положительная разность моментов. Опять выигрыша нет! Замкнутый круг! И это не случайно — такой круг в той или иной форме будет всегда обнаруживаться во всех моделях тихоходных механических вечных двигателей...
В числах изменение моментов представлено в подробной таблице пошагового изменения моментов — желающие могут сравнить с результатами собственных вычислений.
Колесо со скошенными ящиками
Название несколько неуклюжее, зато достаточно точно отображает суть конструкции, показанной на рисунке. Общая идея всё та же — при неизменной массе груза плечо (расстояние от оси колеса до его центра масс) при рабочем ходе больше, чем при обратном, что и обеспечивает нужную разность вращающих моментов. В отличие от колеса Бхаскары, здесь нежелательный вращающий момент уменьшается уже в самом начале обратного хода, а увеличивается в самом начале рабочего хода. Поможет ли это получить выигрыш?
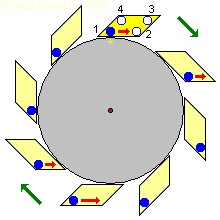 Колесо со скошенными ящиками. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта. Цифрами обозначены положения шара в ящике на разных фазах полного цикла работы элемента.
Расчёт здесь более сложный — для этого нам придётся рассчитать 4 фазы движения. В качестве базового радиуса возьмём расстояние R от оси колеса до центра масс груза в первой фазе. Предположим, что стороны ящика скошены под углом 45°, при этом перемещение груза вдоль тангенциальной (параллельной ободу) стороны составляет 20% R, а при перевороте ящика центр масс груза смещается на 10% R от бывшего «дна» ящика. Выбор точки отсчёта позволяет свести задачу к решению прямоугольных треугольников с известными катетами. Расстояние до центра в этом случае равно гипотенузе этого треугольника, а угол опережения — арктангенсу отношения меньшего катета a (тангенциального относительно обода) к большему b (ориентированному по нормали, т.е. перпендикулярно ободу). Предположив, что перемещение груза длится время, соответствующее повороту на 1°, получаем следующую таблицу.
| Фаза |
Углы точки отсчёта для фазы |
Длина тангенциального катета a |
Длина нормального катета b |
Угол опережения точки отсчёта |
Расстояние до оси колеса |
| 1 |
226°..0° |
0% |
100% |
0.0° |
100.0% |
| 2 |
1°..45° |
20% |
100% |
11.3° |
102.0% |
| 3 |
46°..180° |
30% |
110% |
15.3° |
114.0% |
| 4 |
181°..225° |
10% |
110% |
5.2° |
110.4% |
Момент здесь превышает 100%, поскольку в данном случае в качестве эталона было выбрано не максимальное, а минимальное расстояние от оси, но на расчёт нормированной работы это не влияет — на то она и нормированная! В результате расчёта получаем следующую картину.
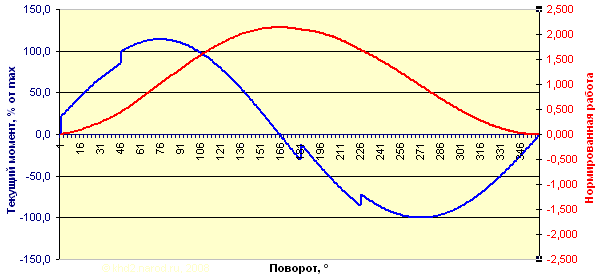 Текущий момент и суммарная нормированная работа одного элемента в колесе со скошенными ящиками.
Нормированная работа за цикл от одного элемента: -0,007141.
Как и в случае колеса Бхаскары, здесь в первой половине графиков (рабочий ход) часть полезной работы уже «съедается» при поднятии шара из самого нижнего положения, в которое он попадает раньше, чем точка отсчёта пройдёт половину пути. Да и в начале обратного хода — на 3-й фазе — положение шара ещё не обеспечивает минимального момента. В результате эти нюансы, действительно не очень большие, всё-таки съедают всё положительное, что мы получили во время рабочего хода — ведь и разность моментов здесь не так велика, как в предыдущей конструкции. Как и в предыдущем случае, попытки изменить наклоны и соотношения положительного результата не дадут — выигрывая в одном, будем терять в другом, а в общем, как и положено в замкнутой системе без учёта потерь на трение, суммарная работа за цикл будет примерно равна нулю — за вычетом погрешностей, обусловленных особенностями использованного численного метода моделирования.
В числах изменение моментов представлено в отдельной таблице пошагового изменения моментов. Кстати, если предположить, что высота ящиков так мала, что шар может кататься только вдоль тангенциальной стороны, то мы приходим к той же кинематике груза, что и в колесе Бхаскары при большом наклоне спиц (когда соотношение R1 / R2 приближается к 100%)!
Колесо с качающейся направляющей
Итак, в предыдущих конструкциях выигрыша получить не удалось, не в последнюю очередь из-за того, что часть полезной работы съедалась ещё во время рабочего хода. Попробуем же создать конструкцию, где весь положительный вращающий момент сосредоточен в середине рабочего хода, а к началу обратного хода груз уже давно переместился на минимальное расстояние от оси вращения.
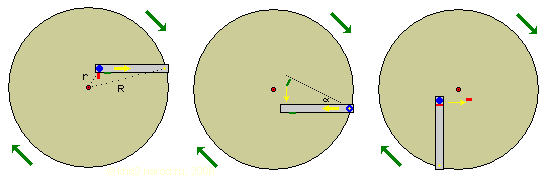 Три фазы рабочего цикла колеса с качающейся направляющей. Жёлтым крестиком отмечено начальное положение точки отсчёта, совпадающее с осью качания направляющей, зелёный цвет показывает открытое состояние фиксаторов, красный — закрытое.
Здесь во время рабочего хода груз скатывается из центра колеса к его ободу, увеличивая вращающий момент, а немного погодя направляющая падает вниз, груз по ней возвращается обратно, и его вращающий момент становится минимальным ещё до начала обратного хода. Фиксаторы направляющей и груза легко реализуются с помощью защёлок и рычажков, выходящих на тыльную сторону колеса и переключаемых с помощью специальных направляющих, причём потери на трение и переключение будут незначительны — ведь в момент освобождения защёлок вес груза не давит на фиксаторы.
В данном случае придётся рассчитать 3 фазы положения груза. Для расчёта предположим, что перемещение груза длится время, соответствующее повороту на 1°, а направляющая становится горизонтальной (шар начинает катиться), когда угол между вертикалью и направлением от оси вращения к грузу равен 45°. В этом случае минимальное расстояние от оси колеса до груза r = (R · tg(α / 2)) / ((tg(α / 2) + 1) · sin(45°)), где R — расстояние от оси колеса до оси качания направляющей, а α — полный угол качания направляющей. Если ось качания направляющей совпадает с центром масс груза в рабочем положении, то приняв плечо при рабочем ходе за 100%, а полный угол качания направляющей равным 30°, получаем следующую таблицу.
| Фаза |
Углы точки отсчёта для фазы |
Угол опережения точки отсчёта |
Расстояние до оси колеса |
| 1 |
196°..75° |
-45° |
29.9% |
| 2 |
76°..105° |
0° |
100.0% |
| 3 |
106°..195° |
45° |
29.9% |
В результате расчёта видно, что полезной работы получить опять не удалось, и графики позволяют наглядно увидеть, почему это происходит.
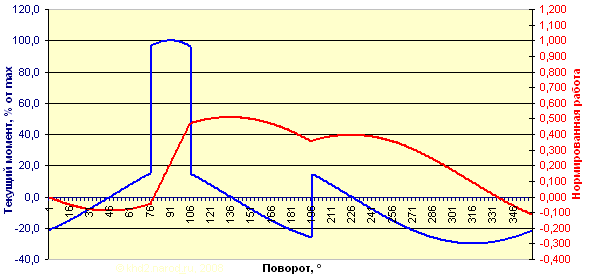 Текущий момент и суммарная нормированная работа одного элемента в колесе с качающейся направляющей.
Нормированная работа за цикл от одного элемента: -0,113248.
Всё дело в том, что, возвратившись к оси, груз существенно опережает точку отсчёта, и когда во время обратного хода направляющая возвращается в исходное положение, он дважды проходит очень существенный угол с отрицательным вращающим моментом, что и съедает весь небольшой выигрыш от положительной разности моментов на рабочем ходу. Конкретные численные значения приведены в отдельной таблице пошагового изменения моментов.
Теперь попробуем максимально удлинить направляющую, так чтобы шар начинал движение тогда, когда он находится точно над осью. Здесь перемещение направляющей проходит через ось, однако технически это несложно реализовать, если закрепить колесо консольно — лишь за один конец оси, а другой конец оси упрятать заподлицо с той его поверхностью, по которой перемещается направляющая. Такое изменение конструкции очень упрощает расчёт, и, кстати, здесь становится абсолютно очевидной жесткая геометрическая связь между углом качания направляющей и плечом груза в положении обратного хода. В случае, если ось качания направляющей совпадает с центром масс груза в рабочем положении, r = R · sin(α / 2), где r — плечо в положении обратного хода, R — плечо при рабочем ходе, α — полный угол качания направляющей.
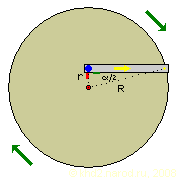 Колесо с удлинённой качающейся направляющей.
Как и в первом варианте, предположим, что перемещение груза длится время, соответствующее повороту на 1°, приняв плечо при рабочем ходе за 100%, а полный угол качания направляющей равным 30°. Тогда получаем следующую таблицу.
| Фаза |
Углы точки отсчёта для фазы |
Угол опережения точки отсчёта |
Расстояние до оси колеса |
| 1 |
196°..75° |
-90° |
25.9% |
| 2 |
76°..105° |
0° |
100.0% |
| 3 |
106°..195° |
90° |
25.9% |
Здесь положение ещё несколько ухудшилось, поскольку углы опережения и отставания груза возросли, а разность моментов увеличилась не так сильно. Конкретные численные значения приведены в отдельной таблице пошагового изменения моментов.
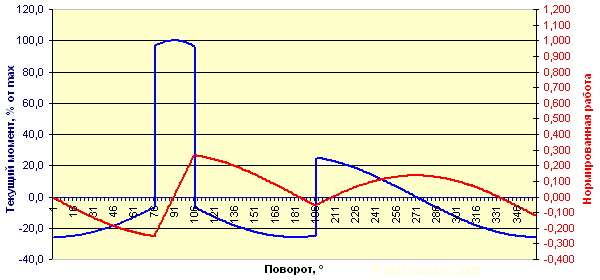 Текущий момент и суммарная нормированная работа одного элемента в модифицированном колесе с качающейся направляющей.
Нормированная работа за цикл от одного элемента: -0,121143.
Результат снова неутешительный! При попытке изменить другие соотношения частей конструкции мы вновь попадаем в заколдованный круг — если мы увеличим угол, в течение которого имеем большой положительный вращающий момент, то неизбежно на столько же увеличим и отрицательный момент во время обратного хода!
Резюме
Итак, все рассмотренные здесь конструкции со свободно катающимися шарами не дают выигрыша, причём основной причиной является опережение грузом точки отсчёта при рабочем ходе и необходимость возврата его в исходное положение на обратном ходу, когда некоторые участки траектории с отрицательным вращающим моментом груз, по сути, проходит дважды — именно это и съедает всю полезную работу, полученную во время рабочего хода.
Кстати, обратите внимание на то, что все результаты в замкнутом цикле получаются не близкими к нулю, а с достаточно большими отрицательным значениями. И это не случайность и не погрешность расчёта — дело в том, что движение шаров во всех рассмотренных конструкциях начинается плавно, но завершается резкой остановкой с неупругим ударом о стенку или ограничитель. При этом кинетическая энергия шара за счёт деформации материалов в момент удара превращается в тепловую, безвозвратно покидая «механический» цикл. Эти потери и обуславливают заметно отрицательный результат, хотя в расчётах этот фактор в явном виде нигде не учитывается!
Может быть, поможет принудительное перемещение грузов на рычагах?
♦
|